结构力学课件同济大学-朱慈勉教学提纲.ppt

结构力学课件同济大学-朱慈勉 ３、结构计算简图的几个要点：空间杆件结构的平面简化杆件构件的简化：以杆件的轴线代替杆件；杆件之间连接的简化：理想结点代替杆件与杆件之间的连接。１）铰结点：汇交于一点的杆端是用一个完全无磨擦的光滑铰连结。铰结点所连各杆端可独自绕铰心自由转动，即各杆端之间的夹角可任意改变。２）刚结点：汇交于一点的杆端是用一个完全不变形的刚性结点连结，形成一个整体。刚结点所连各杆端相互之间的夹角不能改变。３）组合结点（半铰)：刚结点与铰结点的组合体。 结构与支承物连接的简化：　以理想支座代替结构与其支承物（一般是大地）之间的连结。１）活动铰支座：　允许沿支座链杆垂直方向的微小移动。沿支座链杆方向产生约束力。２）固定铰支座：　允许饶固定铰铰心的微小转动。过铰心产生任意方向的约束力（分解成水平和竖直方向的两个力）。３）固定支座：　不允许有任何方向的移动和转动，产生水平、竖直及限制转动的约束力。 §1-3杆件结构的分类1、按结构的受力特点分类：　梁：由水平（或斜向）放置杆件构成。梁构件主要承受弯曲变形，是受弯构件。刚架：不同方向的杆件用结点（一般都有刚结点）连接构成。刚架杆件以受弯为主，所以又叫梁式构件。桁架：由若干直杆在两端用铰结点连接构成。桁架杆件主要承受轴向变形，是拉压构件。　组合结构：由梁式构件和拉压构件构成。拱：一般由曲杆构成。在竖向荷载作用下有水平支座反力。2、按计算方法分类：　　静定结构,超静定结构。 §1-4荷载分类１、按作用时间分类：恒载：永久作用在结构上。如结构自重、永久设备重量。活载：暂时作用在结构上。如人群、风、雪（在结构上可占有任意位置的可动荷载）及车辆、吊车（在结构上平行移动并保持间距不变的移动荷载）。２、按作用性质分类：静力荷载：荷载由零加至最后值，且在加载过程中结构始终保持静力平衡，即可忽略惯性力的影响。动力荷载：荷载（大小、方向、作用线）随时间迅速变化，并使结构发生不容忽视的惯性力。３、按与结构的接触分类：直接荷载，间接荷载。 第二章平面体系的几何组成分析§2-1概　述平面杆件结构，是由若干根杆件构成的能支承荷载的平面杆件体系，而任一杆件体系却不一定能作为结构。本节内容：研究结构的组成规律和合理形式。前提条件：不考虑结构受力后由于材料的应变而产生的微小变形，即把组成结构的每根杆件都看作完全不变形的刚性杆件。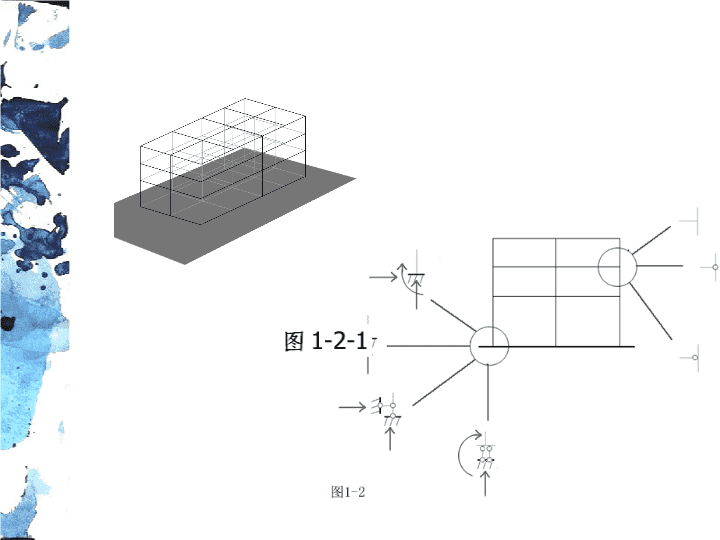一、术语简介（图２-1-1）１、几何不变体系：在荷载作用下能保持其几何形状和位置都不改变的体系称之。２、几何可变体系：在荷载作用下不能保持其几何形状和位置都不改变的体系称之。 ３、刚片：假想的一个在平面内完全不变形的刚性物体叫作刚片。在平面杆件体系中，一根直杆、折杆或曲杆都可以视为刚片，并且由这些构件组成的几何不变体系也可视为刚片。刚片中任一两点间的距离保持不变，既由刚片中任意两点间的一条直线的位置可确定刚片中任一点的位置。所以可由刚片中的一条直线代表刚片。 二、研究体系几何组成的任务和目的：１、研究结构的基本组成规则，用及判定体系是否可作为结构以及选取结构的合理形式。２、根据结构的几何组成，选择相应的计算方法和计算途径。§2-2平面体系的自由度一、自由度的概念体系可独立运动的方式称为该体系的自由度。或表示体系位置的独立坐标数。平面体系的自由度：用以确定平面体系在平面内位置的独立坐标数。 （图2-2-2）上３所示，为平面内一根链杆ＡＢ，其一端Ａ和大地相连，显然相对于大地来说这根链杆在平面内只有一种运动方式，即作绕Ａ点转动，所以该体系只有一个自由度。同时又可看到，如果用链杆ＡＢ与水平坐标的夹角作为表示该体系运动方式的参变量，即表示该体系运动中任一时刻的位置，表示体系位置的参变量数与体系的自由度数也是相等的。所以，该体系的自由度数为１个。平面内最简体系的自由度数：一个点：在平面内运动完全不受限制的一个点有２个自由度。一个刚片：在平面内运动完全不受限制的一个刚片有３个自由度。（图２-2-1） 二、约束概念　当对体系添加了某些装置后，限制了体系的某些方向的运动，使体系原有的自由度数减少，就说这些装置是加在体系上的约束。约束，是能减少体系自由度数的装置。 １、单约束（见图２-2-2）　连接两个物体（刚片或点）的约束叫单约束。１）单链杆（链杆）（上图）　一根单链杆或一个可动铰（一根支座链杆）具有１个约束。２）单铰（下图）　一个单铰或一个固定铰支座（两个支座链杆）具有两个约束。３）单刚结点　一个单刚结点或一个固定支座具有３个约束。 ２、复约束　连接３个（含３个）以上物体的约束叫复约束。１）复链杆：若一个复链杆上连接了Ｎ个结点，则该复链杆具有(2N-3)个约束，等于(2N-3)个链杆的作用。２）复铰：若一个复铰上连接了Ｎ个刚片，则该复铰具有2(N-1)个约束，等于(N-1)个单铰的作用。 三、多余约束在体系上加上或撤除某一约束并不改变原体系的自由度数，则该约束就是多余约束。 §2-3平面体系的几何组成分析一、几何不变体系的简单组成规则规则一　（两刚片规则）：（图2-3-1）　　　两个刚片用不全交于一点也不全平行的三根链杆相连，组成无多余约束的几何不变体系。　或：两个刚片用一个单铰和杆轴不过该铰铰心的一根链杆相连，组成无多余约束的几何不变体系。＊虚铰的概念：　虚铰是由不直接相连接的两根链杆构成的。虚铰的两根链杆的杆轴可以平行、交叉，或延长线交于一点。　当两个刚片是由有交汇点的虚铰相连时，两个刚片绕该交点（瞬时中心，简称瞬心）作相对转动。从微小运动角度考虑，虚铰的作用相当于在瞬时中心的一个实铰的作用。 规则二　（三刚片规则）：三个刚片用不全在一条直线上的三个单铰（可以是虚铰）两两相连，组成无多余约束的几何不变体系。 ＊铰接三角形规则（简称三角形规则）：平面内一个铰接三角形是无多余约束的几何不变体系。以上三个规则可互相变换。之所以用以上三种不同的表达方式，是为了在具体的几何组成分析中应用方便，表达简捷。规则三　（二元体规则）：二元体特性：在体系上加上或拆去一个二元体，不改变体系原有的自由度数。利用二元体规则简化体系，使体系的几何组成分析简单明了。 例2-3-1对下列图示各体系作几何组成分析(简单规则的一般应用方法)。 二、瞬变体系的概念　１、瞬变体系几何组成特征：在微小荷载作用下发生瞬间的微小的刚体几何变形，然后便成为几何不变体系。 ２、瞬变体系的静力特性：　　在微小荷载作用下可产生无穷大内力。因此，瞬变体系或接近瞬变的体系都是严禁作为结构使用的。瞬变体系一般是总约束数满足但约束方式不满足规则的一类体系，是特殊的几何可变体系。FNAB=FNAC=FP2FNsina=FPFN=FP/(2sina) 例2-3-2对下列图示体系作几何组成分析（说明刚片和约束的恰当选择的影响）. 三、三个刚片的三个单铰有无穷远虚铰情况：两个平行链杆构成沿平行方向上的无穷远虚铰。三个刚片由三个单铰两两相连，若三个铰都有交点，容易由三个铰的位置得出体系几何组成的结论。当三个单铰中有或者全部为无穷远虚铰时，可由分析得出以下依据和结论：１、当有一个无穷远虚铰时，若另两个铰心的连线与该无穷远虚铰方向不平行，体系几何不变；若平行，体系瞬变。２、当有两个无穷远虚铰时，若两个无穷远虚铰的方向相互不平行，体系几何不变；若平行，体系瞬变。３、当有三个无穷远虚铰时，体系瞬变。 例2-3-3对下列图示体系作几何组成分析。 例2-3-4对图示各体系作几何组成分析。 四、有多余约束的几何不变体系：拆除约束法：去掉体系的某些约束，使其成为无多余约束的几何不变体系，则去掉的约束数即是体系的多余约束数。１、切断一根链杆或去掉一个支座链杆，相当去掉一个约束；２、切开一个单铰或去掉一个固定铰支座，相当去掉两个约束；３、切断一根梁式杆或去掉一个固定支座，相当去掉三个约束；４、在连续杆（梁式杆）上加一个单铰，相当去掉一个约束。 例2-3-5对图示各体系作几何组成分析。 第二章　　小　　结一、本章要求１、了解几何不变体系、几何可变体系、瞬变体系、刚片、体系的自由度、虚铰、约束及多余约束的概念；２、重点理解并掌握平面几何不变体系的简单组成规则，并能灵活应用到对体系的分析中；二、简单规则应用要点简单规则中的四个要素：刚片个数、约束个数、约束方式、结论。应用简单规则对体系进行几何组成分析的要点是：紧扣规则。即，将体系简化或分步取为两个或三个刚片，由相应的规则进行分析；分析过程中，规则中的四个要素均要明确表达，缺一不可。 三、对体系作几何组成分析的一般途径１、恰当灵活地确定体系中的刚片和约束体系中的单个杆件、折杆、曲杆或已确定的几何不变体系，一般视为刚片。但当它们中若有用两个铰与体系的其它部分连接时，则可用一根过两铰心的链杆代替，视其为一根链杆的作用。２、如果上部体系与大地的连接符合两个刚片的规则，则可去掉与大地的约束，只分析上部体系。３、通过依次从外部拆除二元体或从内部（基础、基本三角形）加二元体的方法，简化体系后再作分析。 第一部分　静定结构内力计算静定结构的特性：１、几何组成特性２、静力特性静定结构的内力计算依据静力平衡原理。第三章　　静定梁和静定刚架§3-1单　跨　静　定　梁单跨静定梁的类型：简支梁、伸臂梁、悬臂梁一、截面法求某一指定截面的内力 １、内力概念内力是结构承受荷载及变形的能力的体现，可理解为在各种外因用下结构内部材料的一种响应。内力是看不见的，但可由结构上受有荷载和结构发生变形（变形体）体现。２、截面法若要求某一横截面上的内力，假想用一平面沿杆轴垂直方向将该截面截开，使结构成两部分；在截开后暴露的截面上用力（内力）代替原相互的约束。对于截开后结构的两部分上，截面上的内力已成为外力，因此，由任一部分的静力平衡条件，均可列出含有截面内力的静力平衡方程。解该方程即将内力求出。 ３、截面内力　截开一根梁式杆件的截面上有三个内力（分量），即：轴力ＦN、剪力ＦQ和弯矩Μ。１、内力的定义ＦN：截面上平行于截面外法线方向的正应力的代数和，一般以受拉为正。ＦQ：截面上垂直于截面法线方向的切应力的代数和，以使隔离体产生顺时针转动为正。Μ：截面上正应力对截面中性轴的力矩代数和，对梁一般规定使其下部受拉为正。 ２）内力计算式（用截面一侧上外力表达的方式）：ＦN＝截面一侧所有外力在杆轴平行方向上投影　　的代数和。左左为正，右右为正。ＦQ＝截面一侧所有外力在杆轴垂直方向上投影的代　　数和。左上为正，右下为正。Μ＝截面一侧所有外力对截面形心力矩代数和。弯　　矩的竖标画在杆件受拉一侧。 例3-1-1求图（a）所示简支梁在图示荷载下截面的内力。解：1）支座反力∑ΜA=0FBy×4﹣10×4×2﹣100×(4/5)×2=0Fby=60kN(↑)∑ΜB=0FAy=60kN(↑)∑Fx=0FAx+100×(3/5)=0FAx=－60kN(←)由　∑Ｆy=0校核，满足。 ２）Ｃ截面内力∑Ｆx=0ＦNC－60=0ＦNC=60kN∑Ｆy=0ＦQC－60+10×1.5=0ＦQC=45kN∑ΜC=0ΜC－60×1.5－10×1.5×(1.5/2)=0ΜC＝101.25kNm（下侧受拉） １）计算支座反力　　去掉梁的支座约束，代以支座约束反力，并假定反力的方向，建立梁的整体平衡方程。２）求C截面的内力　切开过C点的横截面，将梁分成两部分。取左侧部分考虑，其暴露的截面上按规定的内力的正方向将内力示出，建立静力平衡方程。 说明：计算内力要点：１）所取的隔离体（包括结构的整体、截面法截取的局部），其隔离体周围的所有约束必须全部切断并代以约束力、内力。２）对未知外力（如支座反力），可先假定其方向，由计算后所得结果的正负判断所求力的实际方向，并要求在计算结果后的圆括号内用箭线表示实际方向。３）计算截面的内力时，截面两侧的隔离体可任取其一，一般按其上外力最简原则选择。截面内力均按规定的正方向画出。二、荷载与内力的关系　１、内力图概念　表示结构上所有截面的轴力、剪力和弯矩分布的图形称为内力图。作内力图的最基本的方法是，按内力函数作内力图。 １）建立表示截面位置的x坐标２）取x处的（即K截面）以右部分建立平衡方程　　　∑Ｆy=0得梁ＡＣ段的剪力函数：FQk＝70-20x(0≤x≤4)梁ＡＣ段的剪力图是一条斜直线，取该区段内任意两截面的座标值代入函数，既可画出该区段的剪力图。内力函数是分段的连续函数。 ２、荷载与内力的关系微分关系：dFN/dx=-qxdFQ/dx=-qydM/dx=Qd2M/dx2=-qy增量关系：DFN=-FPxDFQ=-FPyDM=m １）微分关系及几何意义：dFN/dx=-qxdFQ/dx=-qydM/dx=Qd2M/dx2=-qy（１）在无荷载区段，ＦQ图为水平直线；当ＦQ≠０时，Μ图为斜直线;当ＦQ＝０时，Μ图为水平直线。（２）在均布荷载区段，ＦQ图为斜直线；Μ图为抛　　物线，且凸向与荷载指向相同。 ２)增量关系及几何意义：DFN=-FPxDFQ=-FPyDM=m(１）水平集中力FPx作用点两侧截面FN图有突变，其突变值等于FPx。FQ图和Μ图不受影响。（２）竖向集中力FPy作用点两侧截面FQ图有突变，其突变值等于FPy。Μ图有折点，其折点的尖角与FPy方向相同；FN图不受影响。（３）集中力偶Μ作用点两侧截面的Μ图有突变，其突变值等于Μ；FN图和FQ图不受影响。 ３、利用荷载和内力关系的几何意义,可由荷载的分布和类型定性地判断或校核区段上的内力图形状以及突变点和突变值的大小。 三、叠加法作弯矩图1、简支梁的弯矩图叠加法 ２、弯矩图叠加的实质：　指弯矩竖标的叠加（而不是图形的简单叠加），当同一截面在两个弯矩竖标在基线不同侧时，叠加后是两个竖标绝对值相减，弯矩竖标画在绝对值大的一侧；当两个竖标在基线同一侧时，则叠加后是两个竖标绝对值相加，竖标画在同侧。　基线接力法概念。３、直杆段弯矩图的区段叠加法直杆区段的弯矩图叠加可利用简支梁的弯矩图叠加法。其步骤是：（１）计算直杆区段两端的最后弯矩值，以杆轴为基线画出这两个值的竖标，并将两竖标连一直线；（２）将所连直线作为新的基线，叠加相应简支梁在跨间荷载作用下的弯矩图。 例3-1-2作图示简支梁的内力图。解：（１）求支座反力　　（２）求控制截面内力取截面Ｃ以左：FQC=70-20×4=－10kNMC=70×4－20×4×2=120kNm(下侧受拉) 取截面ＤＲ以右：　ＦQDB＝－50kNΜＤB＝50×２＝100kNm(下侧受拉)取截面ＤＬ以右：ＦQDC＝－50＋40＝－10kN(3）作内力图 区段叠加法求Ｅ、Ｄ截面弯矩；ΜE＝20×42/8＋120/2＝100kNm(下侧受拉)ΜＤ＝40×4/4＋120/2＝100kNm(下侧受拉)说明：集中力或集中力偶作用点，注意对有突变的　　内力应考虑分两侧截面分别计算。 例3-1-3求作图示伸臂梁的ＦＱ、Ｍ图。分析：仅有竖向荷载作用时，梁的内力只有弯矩和剪　力。剪力图的控制截面在Ｃ、ＤＬ和ＤＲ，而弯矩　图取截面Ｃ即可，综合考虑，取控制截面为截面Ｃ、　ＤＬ和ＤＲ。 解：（１）支座反力　梁的整体平衡方程∑ΜＡ=0FＢy=140.67kN(↑)∑ΜＢ=0FＡy=27.33kN(↑)∑Ｆx=0FＡx=36kN(→)由∑Ｆy=0校核，满足。（2）计算控制截面的剪力并作FQ图取支座Ｂ以左：FQBC=60×4/5=48kN取支座Ｂ以左：FQBD=60×4/5–140.67=－92.67kN (3)计算控制截面的弯矩并作Ｍ图取截面ＣL以左：ＭＣＡ＝27.33×4－20×4×2=－50.68kNm(上侧受拉)取截面ＣR以左：ＭＣB＝27.33×4－20×4×2+100=49.32kNm(下侧受拉)取截面B以右：ＭＣB＝ＭＣB=60×4×2/5=96kNm(上侧受拉） 例3-1-4比较图示斜梁和简支梁的异同。分析：（１）支座反力相同。（２）两梁的内力由内力函　　数比较简支梁：F0Nx=0F0Qx=ql/2－qxM0x=qlx/2－qx2/2斜梁:FNx=－(ql/2qx)sina=－F0QxsinaFQx=(ql/2－qx)cosa=F0QxcosaMx=qlx/2－qx2/2=M0x 单跨静定梁小结要求：　１）理解内力、内力图的概念；　２）了解梁的主要受力、变形特点；　３）理解并掌握截面法计算内力的方法；　４）熟练掌握用叠加法做直杆段的弯矩图。本节难点及重点：　１）内力正、负号的判断；　２）叠加法做弯矩图。 §3-2多跨静定梁 多跨静定梁由相互在端部铰接、水平放置的若干直杆件与大地一起构成的结构。一、多跨静定梁的组成及传力特征对上图所示梁进行几何组成分析：　　ＡＤ杆与大地按两个刚片的规则组成无多余约束的几何不变体，可独立承受荷载；然后杆ＤＦ和杆ＦＧ也分别按两个刚片的规则依次扩大先前已形成的几何不变体。显然，杆ＤＦ是依赖于Ｄ以右的部分才能承受荷载，而杆ＦＧ是依赖于Ｆ以右的部分才能承受荷载的。或者说，杆ＦＧ被杆ＤＦ支承，杆ＤＦ被杆ＡＤ支承。根据各杆之间这种依赖、支承关系，引入以下两个概念： 基本部分：结构中不依赖于其它部分而独立与大地形成几何不变的部分。附属部分：结构中依赖基本部分的支承才能保持几何不变的部分。把结构中各部分之间的这种依赖、支承关系形象的画成如图示的层叠图，可以清楚的看出多跨静定梁所具有的如下特征：１)组成顺序：先基本部分，后附属部分；２)传力顺序：先附属部分，后基本部分。由于这种多跨静定梁的层叠图象阶梯，可称为阶梯形多跨静定梁。 二、多跨静定梁的内力计算多跨静定梁的内力总能由静力平衡条件求出。关键是按怎样的途径使计算概念清晰、简明。　例3-2-1计算图示多跨静定梁，并作内力图。 解：按层叠图依次取各单跨梁计算∑MA=0FCy×4+(10－5×√2×√2/2)×6+20=0FCy=－12.5kN(↓)∑MC=０FAy×4－20+(5×√2×√2/2－10)×2=0FAy=7.5kN(↑)∑Fx=0FAx+5×√2×√2/2=0FAx=－5kN(←) 说明：　（１）按层叠图从上往下的顺序，画各单跨梁的受力图，并按这个顺序逐一计算各单跨梁的约束力。杆ＦＧ的约束力有３个，如简支梁的计算。杆ＤＦ上没有直接作用的外荷载（注意铰Ｄ上作用的集中荷载FP可放在铰的任意侧），但在Ｆ处有杆ＦＧ部分传来的已知约束力FPy。该杆的计算相当于伸臂梁的计算，其上的荷载即是由其上的附属部分由约束处传来的已知约束力。杆ＡＤ是整个梁的基本部分，有三个与大地相连的待求的支座约束力，其上除了有在Ｄ处由Ｄ以右部分传来的已知约束力，还有直接作用的外荷载FP和m。该杆仍是伸臂梁的计算。 （２）将所有单根梁的约束力求得后，即可将各单跨梁的内力图作出后汇集，也可先汇集成整体再一次作内力图。注意ＡＣ段上集中力偶作用时弯矩图的叠加特点。（３）当多跨静定梁的附属部分上有外荷载时，该外荷载将使该附属部分产生内力，并传给它以下的基本部分使其也产生内力；当在其基本部分上有外荷载时，该外荷载仅使该基本部分（及以下）产生内力，对其上的附属部分不产生内力。 例3-2-2分析图示多跨静定梁可分解成单跨梁分别计算的条件，并作梁的FQ、M图。 分析：（１）图示梁的荷载以及约束的方向，是竖向平行力系。一个平面平行力系只能列两个独立的平衡方程，解两个未知数。（２）杆ＣＥ有两个与大地相连的竖向支座链杆，当仅在竖向荷载作用下时，可维持这个平行力系的平衡。所以，杆ＣＥ在仅有竖向荷载的作用下，可视为与杆ＡＢ同等的基本部分。 解：（１）画层叠图　　（２）计算各单跨梁的约束力　　按层叠图以次画出各单跨梁的受力图，注意杆ＢＣ在杆端只有竖向约束力，并按由上向下的顺序分别计算。（３）作内力图 说明：本例中杆ＢＣ是不直接与大地相连的杆件，　称这类杆为有悬跨多跨静定梁。当仅有竖向荷载作用时，悬跨梁可视为附属部分；当是任意的一般荷载作用时，杆ＢＣ不能视为附属部分，杆ＣＥ部分也不能作为基本部分。多跨静定梁小结了解多跨静定梁两种基本类型的几何组成特点。多跨静定梁分层计算的目的，为了不解联立方程。　计算要点：按先附属，后基本的顺序。 §3-2多跨静定梁 多跨静定梁由相互在端部铰接、水平放置的若干直杆件与大地一起构成的结构。一、多跨静定梁的组成及传力特征对上图所示梁进行几何组成分析：　　ＡＤ杆与大地按两个刚片的规则组成无多余约束的几何不变体，可独立承受荷载；然后杆ＤＦ和杆ＦＧ也分别按两个刚片的规则依次扩大先前已形成的几何不变体。显然，杆ＤＦ是依赖于Ｄ以右的部分才能承受荷载，而杆ＦＧ是依赖于Ｆ以右的部分才能承受荷载的。或者说，杆ＦＧ被杆ＤＦ支承，杆ＤＦ被杆ＡＤ支承。根据各杆之间这种依赖、支承关系，引入以下两个概念： 基本部分：结构中不依赖于其它部分而独立与大地形成几何不变的部分。附属部分：结构中依赖基本部分的支承才能保持几何不变的部分。把结构中各部分之间的这种依赖、支承关系形象的画成如图示的层叠图，可以清楚的看出多跨静定梁所具有的如下特征：１)组成顺序：先基本部分，后附属部分；２)传力顺序：先附属部分，后基本部分。由于这种多跨静定梁的层叠图象阶梯，可称为阶梯形多跨静定梁。 二、多跨静定梁的内力计算多跨静定梁的内力总能由静力平衡条件求出。关键是按怎样的途径使计算概念清晰、简明。　例3-2-1计算图示多跨静定梁，并作内力图。 解：按层叠图依次取各单跨梁计算∑MA=0FCy×4+(10－5×√2×√2/2)×6+20=0FCy=－12.5kN(↓)∑MC=０FAy×4－20+(5×√2×√2/2－10)×2=0FAy=7.5kN(↑)∑Fx=0FAx+5×√2×√2/2=0FAx=－5kN(←) 说明：　（１）按层叠图从上往下的顺序，画各单跨梁的受力图，并按这个顺序逐一计算各单跨梁的约束力。杆ＦＧ的约束力有３个，如简支梁的计算。杆ＤＦ上没有直接作用的外荷载（注意铰Ｄ上作用的集中荷载FP可放在铰的任意侧），但在Ｆ处有杆ＦＧ部分传来的已知约束力FPy。该杆的计算相当于伸臂梁的计算，其上的荷载即是由其上的附属部分由约束处传来的已知约束力。杆ＡＤ是整个梁的基本部分，有三个与大地相连的待求的支座约束力，其上除了有在Ｄ处由Ｄ以右部分传来的已知约束力，还有直接作用的外荷载FP和m。该杆仍是伸臂梁的计算。 （２）将所有单根梁的约束力求得后，即可将各单跨梁的内力图作出后汇集，也可先汇集成整体再一次作内力图。注意ＡＣ段上集中力偶作用时弯矩图的叠加特点。（３）当多跨静定梁的附属部分上有外荷载时，该外荷载将使该附属部分产生内力，并传给它以下的基本部分使其也产生内力；当在其基本部分上有外荷载时，该外荷载仅使该基本部分（及以下）产生内力，对其上的附属部分不产生内力。 例3-2-2分析图示多跨静定梁可分解成单跨梁分别计算的条件，并作梁的FQ、M图。 分析：（１）图示梁的荷载以及约束的方向，是竖向平行力系。一个平面平行力系只能列两个独立的平衡方程，解两个未知数。（２）杆ＣＥ有两个与大地相连的竖向支座链杆，当仅在竖向荷载作用下时，可维持这个平行力系的平衡。所以，杆ＣＥ在仅有竖向荷载的作用下，可视为与杆ＡＢ同等的基本部分。 解：（１）画层叠图　　（２）计算各单跨梁的约束力　　按层叠图以次画出各单跨梁的受力图，注意杆ＢＣ在杆端只有竖向约束力，并按由上向下的顺序分别计算。（３）作内力图 说明：本例中杆ＢＣ是不直接与大地相连的杆件，　称这类杆为有悬跨多跨静定梁。当仅有竖向荷载作用时，悬跨梁可视为附属部分；当是任意的一般荷载作用时，杆ＢＣ不能视为附属部分，杆ＣＥ部分也不能作为基本部分。多跨静定梁小结了解多跨静定梁两种基本类型的几何组成特点。多跨静定梁分层计算的目的，为了不解联立方程。　计算要点：按先附属，后基本的顺序。 §3-3静定刚架刚架一般指由若干横（梁或斜梁）杆、竖（柱）杆构成的，可围成较大空间的结构形式。刚架的杆件是以弯曲变形为主的梁式杆为主。刚架的特点在于它的刚结点。刚架可按支座形式和几何构造特点分为：简支刚架、悬臂刚架、三铰刚架和复合刚架。前三类是可仅用一次两各刚片或三个刚片的规律组成的几何不变体，可统称为简单刚架；而最后一类是多次用两各刚片或三个刚片的规律确定的几何不变体，将其称为复合刚架。显然，简单刚架的分析是复合刚架分析的基础。 静定刚架的计算步骤：（１）计算支座反力（或约束力）；（２）计算杆端截面内力（简称杆端力）和控制截面内力；（３）画各内力图。例3-3-1计算图示静定刚架的内力，并作内力图。分析：图示刚架由3个支座链杆按两个刚片的规则与大地相连，这种形式的刚架为简单刚架。由于其与简支梁的支座类似，又可称简支刚架。 解：（１）求支座反力由整体平衡：∑MA=0FDy×4－40×２　　　　－20×4×2＝0FDy＝60kN(↑)∑MO=0FAy×4－40×2＋20×4×2＝0FAy＝-20kN(↓)∑Fx=0FAx－20×4＝0FAx＝80kN(←)由∑Ｆy=0校核，满足。 （２）计算杆端力取AB杆B截面以下部分，计算该杆Ｂ端杆端力：　∑Fx=0FQBA+20×4－80=0FQBA=0∑Fy=0FNBA-20=0FNBA=20kN∑MB=0MBA+20×4×2-80×4=0MBA=160kNm(右侧受拉) 取BD杆B截面以右部分，计算该杆B端杆端力：∑Fx=0FNBD=0∑Fy=0FQBD－40+60=0FQBD=－20kN∑MB=0MBD+40×2－60×4=0MBD=160kNm(下侧受拉)由结点B校核　∑Fx=0∑Fy=0∑MB=0满足。 ３）绘制内力图　由已求得各杆端力，分别按各杆件作内力图。弯矩图可由已知杆端弯矩，按直杆段的区段叠加法作杆件的弯矩图。说明：在刚架中，各杆件杆端是作为内力的控制截面的。杆端力，即杆端内力。　刚架的内力正负号规定同梁。　为了区分汇交于同一结点的不同杆端的杆端力，用内力符号加两个下标（杆件两端结点编号）表示杆端力。如用MBA表示刚架中AB杆在B端的弯矩。 例3-3-2计算图示悬臂刚架，并作内力图。分析：悬臂刚架的特点是，支座反力集中在刚架的　一个杆端，因此可由截面的悬臂一侧部分的平衡条件求出该截面的全部内力，即不需计算支座反力。 1)计算各杆端弯矩，并作弯矩图MBC=10×3×3/2=45kNm(上侧受拉)MBD=5×2=10kNm(左侧受拉)MBA=10×3×3/2－5×2=35kNm(左侧受拉)MA=10×6×3－5×6=150kNm(左侧受拉) (2)计算各杆端剪力，并作剪力图：FQBC=10×3=30kNFQBD=－5kN∑MA＝0FQBA×5+35+10×3×3/2=0FQBA=－16kN∑MB＝0FQAB×5－150－10×3×3/2=0FQAB=39kN (3)计算各杆端轴力，并作轴力图：由结点Ｂ的平衡条件，建立沿ＡＢ杆方向的投影方程，得：FNBA+5×3/5+30×4/5=0FNBA=－27kNFNAB+20+10×3×4/5=0FNAB=－44kN 说明：　本例计算和作内力图的过程是：弯矩图→剪力图→轴力图。当刚架上所有的外力已知时先作弯矩图；再截开杆件两端取出杆件为隔离体，对两杆端截面形心分别建立力矩方程求出杆端剪力，作剪力图；最后取结点为隔离体，利用结点的投影平衡方程求杆端轴力，作轴力图。 例3-3-3求图示三铰刚架的支座反力。分析：三铰刚架共有四个支座反力，除了利用整体的三个平衡方程，还要考虑铰Ｃ（两侧截面）处弯矩为零的条件。解：由刚架整体平衡条件：∑MA=0FBx×2+FBy×4－20×2×1－40×2－10=0由铰Ｃ右侧：∑MC＝0FBx×2-FBy×2+10=0 整理后得关于支座Ｂ上两个支座反力的联立方程：FBx+2FBy--65=0解得:FBy=23.33kN(↑)FBx-FBy+5=0FBx=18.33kN(←)再由刚架整体的平衡条件，求Ａ支座的两个支座反力：∑Fx=0FAx=18.33－40=－21.67kN(←)∑Fy=0FBx=－23.33+40=16.67kN(↑) 说明：本例研究的三铰刚架的三个铰的相对位置可　　以是任意的，因此是这类（有推力）结构的一　　般形式，它的支座反力的计算方法也具有一般　　性。容易看出，本例求支座反力时必须解联立　　方程。本例采用的方法的原则是，集中先求一　　个铰的两个约束力。即以另外两个铰的铰心为　　矩心分别建立关于这两个约束力的二元一次联　　立方程，求解后再计算其它铰处的约束力。 例3-3-4计算图示刚架，并作其弯矩图。分析：图示刚架是由基本部分AGFB和附属部分EDC构成的复合刚架，可按多跨静定梁先附属后基础的顺序计算。 解：（１）计算ＥＤＣ部分的约束力　∑ME＝0FCy=10×4×2/4=20kN(↑)∑Fx=0FEx=10×4=40kN(↑)∑Fy=0FEy=－FCy=－20kN(↓) (２）计算ＡＧＦＢ部分的约束力　根据作用和反作用定理，由上面得出的Ｅ铰处的约束力要反向作用到ＡＧＦＢ部分上按实际方法示出。∑MA＝0FBy=(20×4-40×4-30×6)/4=-65kN(↓)∑MB＝0FAy=(40×4+30×6)/4=85kN(↑)∑Fx=0FAx=70kN(→)由　∑Fy=0校核，满足。(3)作弯矩图 例3-3-5计算图示刚架，并作弯矩图。分析：这是复合刚架，基本部分为内部GKHDJC，附属部分为两侧的三铰刚架GIEAC和HLFBD。可以看出，刚架及刚架上的外力（荷载和支座反力）均对称于中间竖杆KJ。容易分析出，刚架的内力也对称于杆KJ。因此，计算杆KJ及它的任一侧即可由对称性得知另一侧。支座反力见图。 解：（１）求刚架内力计算GIEAC部分：　∑MC＝0FGx=(qa2/2-2qa2)/(2a)=－3qa/4kN(←)∑MG＝0FCx=-(qa/2-2qa2)/(2a)=3qa/4kN(→) 由铰Ｅ以下部分的平衡条件∑ME＝0FC=FCx=3qa/4kN(↓)由铰Ｅ以上部分的平衡条件∑ME＝0FGy=－FG－qa/2=qa/4kN(↓)由该部分的整体平衡条件　∑Fx=0∑Fy=0校核，满足。（３）计算杆端弯矩,作刚架弯矩图MIG＝qa2/4+qa2/2=3qa2/4kN(上侧受拉)MKG＝qa2/4+qa2/2=－qa2/4kN(上侧受拉) 例3-3-6分析下列图示刚架。 静定刚架　小　结１、要求了解组成刚架的构件及构件的受力特征；刚结点的传力、位移特征；简单刚架和复合刚架的概念；内力正负号规定。２、熟练掌握并能灵活地应用静力平衡条件计算简单刚架的内力，进一步巩固直杆的区段叠加法作弯矩图的方法；掌握复合刚架的内力计算和内力图制作方法、途径。３、刚架内力计算基本步骤：（１）计算刚架的支座反力和约束力；（２）计算杆端力；（３）作内力图（弯矩图→剪力图→轴力图）；（４）校核。 第四章静　定　拱（实体三铰拱）§４－１　概　述一、拱的概念　拱的轴线一般是曲线形状，实体拱指由充满密实材料的杆构成的拱。拱的受力特征是，在竖向荷载作用下可产生水平支座反力（水平推力)。具有这类受力特征的结构称为有推力结构。 二、拱的分类１、按具有的铰的数量分类：　　　三铰拱、两铰拱、无铰拱。２、按几何组成（或计算方法）分类：　　　静定拱：三铰拱、带拉杆三铰拱；　　超静定拱：　两铰拱、无铰拱。§4-2三铰拱的内力计算三铰拱的构造及各部名称，及相应于拱的简支梁（相应简支梁）。一、　三铰拱的支座反力（一）、三铰拱的支座反力　三铰拱的支座反力和三铰刚架支座反力的计算方法完全相同，即以其中两个铰分别建立力矩平衡方程，集中计算剩下的一个铰的两个约束力的方法。 当三铰拱的两个底铰在一条水平线上时，其支座反力的计算常采取如下步骤：１、由拱的整体平衡条件求两个竖向支座反力；２、由拱顶铰C任一侧的平衡条件，求在这一侧上的水平支座反力；３、再由拱的整体平衡条件，求另一水平支座反力。 1、∑MA=0FByl–FP1a1–FP2a2–FP3a3=0FBy=(FP1a1+FP2a2+FP3a3)/l(↑)(a)∑MB=0FAyl–FP1b1–FP2b2FP3b3=0FAy=(FP1b1+FP2b2+FP3b3)/l(↑)(b)２、∑MC=0FByl2–FBxf–FP3(l2–b3)=0FBx=[FByl2–FP3(l2–b3)]/f(←)（c)３、∑Fx=0FBx–FAx=0FAx=FBx=FH(d) 说明：上述计算底铰在一条水平线上的三铰拱支座反力的方法和步骤，适用于任意荷载作用下的情况。但两个底铰的水平反力相同仅是在只有竖向荷载作用的情况下。（二）、三铰拱与相应简支梁的几个关系式：　相应简支梁，指与拱的跨度、荷载相同的简支梁。容易得知三铰拱与相应简支梁的如下几个关系式：FAy=F0AyFBy=F0ByFH=M0C/f。(4-2-1)这三个关系式仅在只有竖向荷载作用下成立。　由第三式分析，在拱上作用的荷载和拱的跨度不变的条件下，M0C是一个常数，FH与f得出，拱的推力FH与它的高跨比f/l有关，即当高跨比f/l越小（越大）,则水平推力FH越大（越小）。 二、拱的内力计算　拱的任一截面上一般有三个内力（M,FQ,FN），内力计算的基本方法仍是截面法。与直杆件不同的是拱轴为曲线时，截面法线角度不断改变，截面上内力（FQ,FN）的方向也相应改变。例4-2-1已知图示三铰拱的拱轴方程为y(x)=4fx(l－x)/l2，求支座反力及K截面的内力。解：（１）求支座反力由拱的整体平衡条件：∑MA=0FBy×16–10×12–2×8×4=0FBy=11.5kN(↑)∑MB=0FAy×16–10×4–2×8×12=0FAy=14.5kN(↑) 取铰Ｃ以右部分的平衡条件：∑MC=0FH×4–FBy×8+10×4=0FH=13kN(←) （２）求Ｋ截面的内力　取Ｋ截面以左部分：截面各内力均按正方向画（注意：规定拱的轴力以受压为正；剪力和弯矩的规定仍同前）。　确定Ｋ截面位置参数yK和αK：　将Ｋ截面坐标x=4m代入:y(x)=4fx(l－x)/l2和tanαK=dy/dx=4f(l－2x)/l2得：yK=3mtanαK=0.5则有:αK=26.57°sinαK=0.447cosαK=0.894建立隔离体的平衡方程，求Ｋ截面的内力：　以截面Ｋ的外法线n和切向τ的方向分别建立投影方程，求FNK和FQK： ∑Fn=0FNK–(14.5–2×4)sinαK–13cosαK=0FNK=14.528kN(FNK=F0QKsinαK+FHcosαK) ∑Fτ=0FQK–(14.5–2×4)cosαK+13sinαK=0FQK=0(FQK=F0QKcosαK–FHsinαK) 以Ｋ点为矩心的力矩平衡方程，求MK：　∑MK=0MK+2×4×2+13×3–14.5×4=0得：MK=3kNm(下侧受拉)(MK=M0K–FHyK) 说明：对照上述计算拱内力的三个方程式，可以写出如后面括号中三个内力表达式，即：FNK=F0QKsinαK+FHcosαKFQK=FQKcosαK–FHsinαK（4-2-2）MK=M0K–FHyK上式可作为拱内力的计算公式用，特别是在作拱的内力图时。但须注意以下几点：１、式（4-2-2）要在以拱的左底铰为原点的平面直角坐标中应用，并仅考虑了竖向荷载的作用。２、式中αK为所计算K截面外法线n（或K截面处拱轴切线）与水平x坐标的夹角。如果取αK是与水平方向的锐角考虑，则K截面在左半拱时为正，在右半拱时为负。 ３、带拉杆的三铰拱，其支座反力可由整体的平衡条件完全求得；水平推力由拉杆承受。可将顶铰和拉杆切开，取任一部分求出拉杆中的轴力。三、拱的内力图特征１、拱的内力图特征由式（4-2-2）分析，当拱轴为曲线时。有：（１）不管拱轴区段上是否有分布荷载，拱的各内力图在区段上均为曲线形状；（２）在竖向集中力FP作用点两侧截面，拱的轴力和剪力有突变，突变值分别为FPsinαK和FPcosαK，弯矩图在该点转折；在集中力偶Ｍ作用点两侧截面，弯矩有突变，突变值为Ｍ，轴力和剪力不受影响。（３）由于水平推力对拱的弯矩的影响，拱的弯矩与相应的简支梁的弯矩比较大大的减小。 ２、拱的内力图的制作方法　原则上是将拱沿其跨度平分成若干等份区段，分别计算出每个等分点截面的内力值，然后将各点内力竖标顺序连以光滑曲线即可。但要注意各内力图上的突变和转折特征。　当只有竖向荷载作用时，拱轴上各等分点截面的内力计算，可利用式（4-2-2）制作适当的表格后，再进行由表格表示的各项的计算。 §4-3拱的合理拱轴简介由于拱的水平推力的作用，拱的弯矩与相应的简支梁相比大大减小，所以拱是以受压为主的结构。一、拱的合理拱轴概念：　在某一荷载作用下，沿拱轴所有截面上均无弯矩时的拱轴线称之。二、在竖向荷载下的合理拱轴线　根据拱的合理拱轴的概念，在竖向荷载下的合理拱轴线可由式（4-2-2）中的弯矩式得出，即由MK=M0K–FHyK并令MK=０　得：yK=M0K/FH（4-3-1） 例4-3-1求图示三铰拱的合理拱轴线方程，并分析其合理拱轴的形状。 解：（１）求支座反力　由整体的平衡条件∑MB=0得：FAy×8－FH×2－20×6－10×4×2=0由Ｃ铰以左部分的平衡　∑MC=0得：FAy×4－FH×4－20×2=0联立上两式：4FAy－FH－100=0FAy－FH－10=0解得：FAy=30kN(↑)FH=20kN(→) （２）建立以Ａ支座为原点的直角坐标，由式y=M0/FH分段写出拱的合理拱轴线方程: (0≤x≤2)y=(30/20)x=3x/2(2≤x≤4)y=[30x－20(x－2)]/20=x/2＋2(4≤x≤8)y=[(30x－20(x－2)－10(x－4)2/2]/20=－x2/4＋5x/2－2上式即为竖向荷载作用下的合理拱轴线方程。 说明：由本例结果可知，三铰拱在竖向集中荷载作　　用下的的无荷载区段上，合理拱轴是一条直线，　　并在集中荷载作用点出现转折；在均布荷载作　　用区段上，合理拱轴是一条抛物线。　　　拱的合理拱轴线的形状与相应的简支梁的弯　　矩图相似。静定拱　小结一、、要求了解拱的受力特点；重点掌握两个底铰在一条水平线上的三铰拱的支座反力的计算，及拱轴上指定截面的内力计算；了解拱的内力图的特征及制作方法。二、应掌握拱在任意荷载下的计算，即不限于仅有竖向荷载的情况。所以。拱的内力计算应建立在牢固掌握截面法的基础之上，而不只是运用公式。 此课件下载可自行编辑修改，仅供参考！感谢您的支持，我们努力做得更好！谢谢