中南大学结构力学课件--13结构弹性稳定.ppt

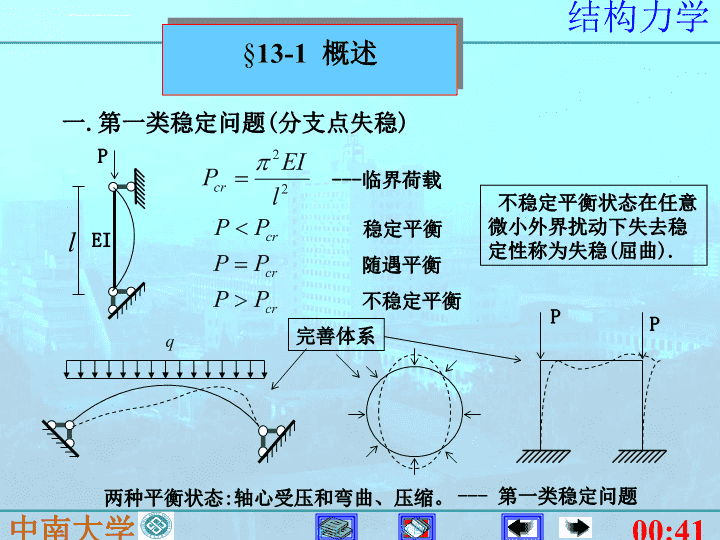
第十三章结构弹性稳定§13-1概述§13-2用静力法确定临界荷载§13-3具有弹性支座压杆的稳定§13-4用能量法确定临界荷载§13-5变截面压杆的稳定§13-6剪力对临界荷载的影响§13-7组合压杆的稳定 §13-8弹性介质上压杆的稳定§13-9圆环及拱的稳定§13-10窄条梁的稳定§13-11用矩阵位移法计算刚架的稳定 13-1概述一.第一类稳定问题(分支点失稳)lEIP---临界荷载稳定平衡随遇平衡不稳定平衡PP不稳定平衡状态在任意微小外界扰动下失去稳定性称为失稳(屈曲).两种平衡状态:轴心受压和弯曲、压缩。---第一类稳定问题完善体系 二.第二类稳定问题(极值点失稳)偏心受压三.分析方法大挠度理论。第二类稳定问题PP有初曲率小挠度理论。静力法能量法四.稳定自由度在稳定计算中,一个体系产生弹性变形时,确定其变形状态所需的独立几何参数的数目,称为稳定自由度。非完善体系P1个自由度PP2个自由度无限自由度 13-2.用静力法确定临界荷载一.一个自由度体系小挠度、小位移情况下：Pl1抗转弹簧A----稳定方程（特征方程）---临界荷载 二.N自由度体系（以2自由度体系为例）----稳定方程---临界荷载lAPlB---失稳形式P11.618 三.无限自由度体系Pl挠曲线近似微分方程为QPQ或令通解为由边界条件得稳定方程 PlQPQ得稳定方程经试算 13-3.具有弹性支座压杆的稳定PlP1练习:简化成具有弹簧支座的压杆PllPlPPk PlAyyxQPQ挠曲线近似微分方程为令通解为边界条件稳定方程解方程可得nl的最小正根 PlAyyxQPQ稳定方程解方程可得nl的最小正根lEIP若若Pl lEIP若若PlPlP 例:求图示刚的临界荷载.正对称失稳反对称失稳正对称失稳时1 例:求图示刚的临界荷载.正对称失稳反对称失稳反对称失稳时01原结构的临界荷载为: 13-4用能量法确定临界荷载一.势能原理2.外力势能1.应变能弯曲应变能P拉压应变能PP剪切应变能外力从变形状态退回到无位移的原始状态中所作的功.y(x)q(x)3.结构势能 结构势能例:求图示桁架在平衡状态下的结构势能.EA=常数.P1llA解:杆件轴力杆件伸长量A点竖向位移外力势能应变能 结构势能P1llA杆件轴力杆件伸长量A点竖向位移外力势能应变能4.势能驻值原理设A点发生任意竖向位移是的函数.杆件伸长量杆件轴力应变能外力势能结构势能 4.势能驻值原理设A点发生任意竖向位移是的函数.杆件伸长量杆件轴力应变能外力势能结构势能在弹性结构的一切可能位移中，真实位移使结构势能取驻值。满足结构位移边界条件的位移对于稳定平衡状态,真实位移使结构势能取极小值. 二.能量法确定临界荷载例一:求图示结构的临界荷载.PlkyP解:应变能外力势能结构势能由势能驻值原理得临界荷载 例二:求图示结构的临界荷载.解:应变能外力势能结构势能lPlP 三.瑞利里兹法PlP应变能外力势能结构势能设将无限自由度化为有限自由度.结构势能则为的多元函数,求其极值即可求出临界荷载. lEIP例:求图示体系的临界荷载.解:1.设精确解: 例:求图示体系的临界荷载.lEIP解:2.设精确解:误差:+21.6%3.设杆中作用集中荷载所引起的位移作为失稳时的位移.l/2l/2Q令误差:+1.3% EIGAlP设弯矩和剪力影响所产生的挠度分别为和同时考虑弯矩和剪力对变形的影响时的挠曲微分方程的建立:二者共同影响产生的挠度为近似的曲率为弯矩引起的曲率为截面形状系数矩形截面为1.2圆形截面为1.11挠曲微分方程为13-6剪力对临界荷载的影响 EIGAlP挠曲微分方程为对于图示两端铰支的等截面杆,有令方程的通解边界条件 EIGAlP对于图示两端铰支的等截面杆,有令方程的通解边界条件稳定方程 EIGAlP稳定方程不计剪变的欧拉临界力修正系数欧拉临界应力对于三号钢,比例极限为200MPa.若取结论:实体杆件中,剪力对临界荷载的影响很小,可略去不计.不计剪力对临界荷载的影响所得到的临界荷载是大还是小? 13-7组合压杆的稳定缀条式缀板式肢杆缀条缀板组合压杆的临界荷载比截面和柔度相同的实体压杆的小,节间数目较多时可用上节推出的实体压杆的临界荷载计算公式作近似计算. 一.缀条式组合压杆z不计肢杆轴变.---水平缀条截面积.---斜杆截面积. zI的计算:I为两根肢杆的截面对z轴的惯性矩.设一根肢杆的截面积为A,对自身形心轴的惯性矩为I1 z若略去横杆影响,两侧都有缀条,则上式为若写成欧拉问题基本形式 若写成欧拉问题基本形式若用r代表两肢杆截面对整个截面形心轴z的回转半径,即并且,一般为,故可取并引入长细比若采用换算长细比,则有 若用r代表两肢杆截面对整个截面形心轴z的回转半径,即并且,一般为,故可取并引入长细比若采用换算长细比,则有上式既是钢结构规范中推荐的缀条式组合压杆换算长细比的公式.