武汉理工大学材料力学课件8 组合变形及连接部分的计算--JK.ppt

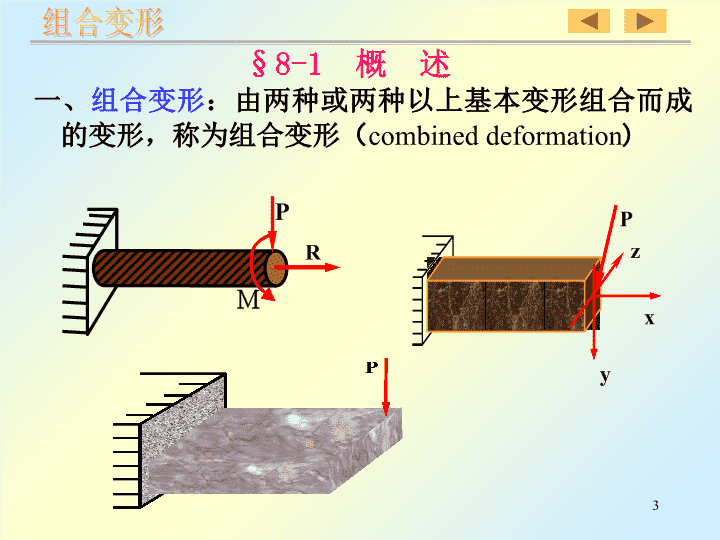
第八章组合变形及连接部分的计算1 §8-1概述§8-2两相互垂直平面内的弯曲§8-3拉伸(压缩)与弯曲§8-4扭转与弯曲第八章组合变形及连接部分的计算组合变形§8-5连接件的实用计算§8-6铆钉连接的计算*§8-7榫齿连接2 组合变形§8-1概述一、组合变形：由两种或两种以上基本变形组合而成的变形，称为组合变形（combineddeformation)3 组合变形hγ4 组合变形5 二、组合变形的研究方法——先分解而后叠加①外力分析，确定基本变形：将外力分解为几组与之静力等效的简单载荷，确定基本变形；②内力分析，确定危险截面：求每个外力分量对应的内力并画内力图，确定危险面；③应力分析，确定危险点：画危险面应力分布图，确定危险点，叠加求危险点应力；组合变形④强度计算：建立危险点的强度条件，进行强度计算。具体步骤：6 §8-2两相互垂直平面内的弯曲斜弯曲：杆件产生弯曲变形后，杆轴线不再位于外力作用平面内。一、正应力的计算：1、将外载沿横截面的两个形心主轴分解，得:组合变形yzFzFyxxzyOlFφ2、梁任意截面上的弯矩为：7 My引起A的应力：Mz引起A的应力：则，F引起的应力为：组合变形yzyzAFzFyxxzyOlFφ3、梁截面上任一点A（y,z）的应力为（考虑坐标符号）：另外，的正负号可由My和Mz引起的变形是拉还是压直接判断。8 D1D2二、中性轴的位置中性轴组合变形yzFzFyFφa令（y0，z0）是中性轴上任一点，则有：显然，中性轴是一条通过坐标原点的直线，可见，中性轴的位置并不依赖于力F的大小，而只与力F和形心主轴y的夹角以及截面几何形状和尺寸有关。三、最大正应力和强度条件在中性轴两侧，距中性轴最远的点为最大拉、压应力点。图中D1、D2两切点应力最大：设其与z轴的夹角为α，则有：应力分布如图所示：9 若横截面周边具有棱角，则无需确定中性轴的位置，直接根据梁的变形情况，确定最大拉应力和最大压应力点的位置。D1D2中性轴yzD2D1中性轴yz组合变形强度条件：10 （2）对于方形、圆形一类的截面，Iy＝Iz，则，此时的挠度不仅垂直于中性轴而且与外力平面重合，为平面弯曲。中性轴yzFφa组合变形wzwy四、挠度的计算w自由端处由Fy引起的挠度为：自由端处由Fz引起的挠度为：则，自由端处由F引起的总挠度为：由上式可见：（1）对于矩形、工字形一类的截面，Iy≠Iz，则，这表示挠度方向垂直于中性轴但与外力平面不重合，为“斜弯曲”。11 例8-2-1矩形截面木檩条如图，跨长L=3m，h=2b，受集度为q=700N/m的均布力作用，[]=10MPa，容许挠度[w]=L/200，E=10GPa，试选择截面尺寸并校核刚度。yzhba=26°q解：①、外力分析——分解q组合变形②、内力分析——求Mzmax、Mymax12 组合变形③、应力分析—求④、强度计算—确定截面尺寸⑤、校核刚度13 组合变形例8-2-2如图所示简支梁由28a号工宇钢制成，已知F=25kN，l=4m，，许用应力[σ]=70MPa，试按正应力强度条件校核此梁。解:(1)将集中力F沿y轴和z轴方向分解14 组合变形28a号工宇钢的抗弯截面模量此梁满足强度要求。15 ABCDx2kNm1kNm组合变形例8-2-3两端铰支矩形截面梁，其尺寸h=80mm,b=40mm,校核梁的强度。xABCD30kNz30kN100mm100mm100mmyzyhb解:(1)画内力图，确定危险截面:+ABCDx2kNm1kNm16 组合变形(2)校核强度:故，梁安全。17 工程实际中，常遇到如下受力的构件：组合变形§8-3拉伸(压缩)与弯曲lF1F2FFM偏心压缩轴向力和横向力同时作用偏心拉伸FFMzMyyz18 组合变形一、轴向力和横向力同时作用xzylF1xF2分析任一截面上应力＋＝F1单独作用时：F2单独作用时：F1、F2共同作用时：19 组合变形特别指出：运用上式计算最大应力时，弯矩M取绝对值，而轴力FN取代数值。强度条件：则则20 组合变形[例8-3-1]最大吊重为P=20kN的简易吊车，如图所示，AB为工字A3钢梁，许用应力[σ]＝100MPa，试选择工字梁型号。ADCBF30°2m1mYAXACABF52kN_FNTxTyT20kN·mM-解：(1)选工字梁为研究对象受力如图所示：分解：画内力图如上：21 由弯矩图和轴力图知：C截面左侧为危险截面。组合变形(2)暂不考虑轴力影响，只按弯曲正应力强度条件初选工字梁型号，有：(3)按压弯组合变形进行校核。初选成功，即选20a号工字梁合适。YAXACABF52kN_FNTxTyT20kN·mM-查型钢表，初选取20a号工字钢，Wz=237cm3，A＝35.5cm222 组合变形二、偏心拉伸（压缩）(1)若F的作用点在杆的一对称轴上，FMFz则强度条件为：23 组合变形FMzMyyzFyz(2)若F的作用点不在杆的任一对称轴上则强度条件为：FMyMz24 [例8-3-2]图示压力机，最大压力F=1400kN，机架用铸铁作成，许用拉应力[σt]=35MPa，许用压应力[σc]=140MPa，试校核该压力机立柱部分的强度。立柱截面的几何性质如下：yc=200mm，h=700mm，A=1.8×105mm2，Iz=8.0×109mm4。解：由图可见，载荷F偏离立柱轴线，组合变形500FFhzycyC其偏心距为：e=yc+500=200+500=700mmFeFNM任一截面上的力如图：其中：25 在偏心拉力F作用下，横截面上由各内力产生的应力如图：可见，立柱符合强度要求。Pey2ycbca组合变形FN=F26 组合变形[例8-3-3]一端固定、具有切槽的杆如图所示，试指出危险点的位置，并求最大应力，已知F=1kN。10501010405Fyz510解：在切槽的截面上的内力有：截面几何性质：危险点在切槽截面的左上角。27 AACBFlaABFMe组合变形§8-4扭转与弯曲(1)分析AB杆，将力F向其B端简化，并画内力图。--TFaMFl由内力图知A为危险截面K1K2(2)画危险截面的应力分布图K1、K2两点为危险点28 组合变形K1K1AK1K2从K1点取一单元体，如图，其中第三强度理论：第四强度理论：即：29 ①、外力分析：外力向形心简化并分解；②、内力分析：每个外力分量对应的内力方程和内力图，确定危险面；③、应力分析：确定危险点；弯扭组合问题的求解步骤：组合变形④、建立强度条件：圆截面弯扭组合圆截面弯扭组合30 组合变形[例8-4-1]图示刚架，两杆在水平面内且相互垂直，受力与刚架平面垂直，F=2kN,l=1m,各杆直径d=10mm，[σ]=70MPa，按最大剪应力理论校核AB杆强度。lFllABCD2FFl-M3Fl+T故：AB杆安全解:（1）将力向AB杆上简化:（2）画AB杆内力图:（3）强度校核:FMeAB31 组合变形[例8-4-2]电机带动一圆轴AB，其中点处装有一个重Q=5kN，直径D=1.2m的胶带轮，胶带紧边张力F1=6kN,松边张力F2=3kN，如轴的许用应力[σ]=50MPa，试按第三强度理论设计轴的直径d。FABCMxMe解:（1）将力向AB轴上简化:（2）画AB轴内力图:（3）强度计算:其中+4.2kN·mM-1.8kN·mT取d=98mmF2l=1.2mABCQF1Dd32 组合变形[例8-4-3]将上例中的胶带由竖直索引改为水平索引，其它不变，试按第三强度理论设计轴的直径d。解:（1）将力向AB轴上简化:（2）画AB轴内力图:（3）强度计算:其中-1.8kN·mT取d=90mmF2F1Dl=1.2mABCQdQABCMxMeFxyz+1.5kN·mMz2.7kN·mMy代数据33 组合变形34 拉压一、概述§8-5连接件的实用计算法螺栓连接铆钉连接销钉连接平键连接榫齿连接35 拉压36 拉压37 拉压38 拉压受力特点：等值、反向、平行，作用线很近。变形特点：位于两力之间的截面发生相对错动。二、剪切的实用计算切应力计算公式：切应力强度条件：假设：切应力均匀分布剪切面上的剪力：Fs=FA为剪切面面积{单剪双剪剪切面：平行于外力作用线且有相互错动趋势的面。FFFFsFFs39 拉压三、挤压的实用计算假设：应力均匀分布实用挤压应力公式：挤压强度条件：*挤压面面积的计算FF挤压：连接件与被连接件接触表面的相互压紧。挤压面：垂直外力作用线且相互挤压的接触面。挤压面为圆柱曲面，用直径平面代替挤压面为平面，按实际平面面积计算40 拉压41 拉压[例8-5-1]已知F=50kN，b=150mm，δ=10mm，d=17mm，a=80mm，[σ]=160MPa，[τ]=120MPa，[σbs]=320MPa，铆钉和板的材料相同，试校核其强度。解：1板的拉伸强度42 拉压3铆钉的剪切强度2板和铆钉的挤压强度强度足够。43 拉压[例8-5-2]一销钉连接如图所示，已知F=18kN，被连接的构件A和B的厚度分别为t=8mm、t1=5mm，销钉直径d=15mm，材料的许用切应力，许用挤压应力，试校核销钉的强度。ABFFtt1t1d解：分析知销钉的受力如图所示。FmmnnmmFsnnFsmmnnFFsFsmmnn挤压面可见销钉有两个剪切面44 拉压FmmnnmmFsnnFsmmnnFFsFs（1）剪切强度校核（2）挤压强度校核由（1）、（2）知，销钉的剪切和挤压强度均符合条件。mmnn挤压面45 [例8-5-3]：拉杆头部尺寸如图所示，已知[τ]=100MPa，许用挤压应力[σbs]=200MPa。校核拉杆头部的强度。拉压D=40h=10d=20F=40kN解：46 [例8-5-4]已知P、a、b、l。计算榫接头的切应力和挤压应力。拉压aaabllFF解：FF47 [例8-5-5]已知铝板的厚度为t，剪切强度极限。为了将其冲成图示形状，试求冲床的最小冲力。拉压aaa3aa48 解：拉压As为六边形的侧面面积49 §8-6铆钉连接的计算拉压50 [例8-6-1]图示钢板铆接件，已知钢板拉伸许用应力[σ]=98MPa，挤压许用应力[σbs]=196MPa，钢板厚度δ=10mm，宽度b=100mm，铆钉直径d=17mm，铆钉许用切应力[τ]=137MPa，挤压许用应力[σbs]=314MPa。若铆接件承受的载荷FP=23.5kN。试校核钢板与铆钉的强度。拉压51 拉伸强度拉压挤压强度解：对钢板52 剪切强度拉压对铆钉挤压强度53 [例8-6-2]托架受力如图所示。已知F＝100kN，铆钉直径d＝26mm。求铆钉横截面最大切应力（铆钉受单剪）。离C点最远的铆钉所受剪力最大拉压解:54 1、在图示杆件中，最大压应力发生在截面上的哪一点，现有四种答案:（A）A点（B）B点（C）C点（D）D点本章习题一、选择题组合变形55 2、在下列有关横截面核心的结论中，是错误的。Ａ、当拉力作用于截面核心内部时，杆内只有拉应力。Ｂ、当拉力作用于截面核心外部时，杆内只有压应力。Ｃ、当压力作用于截面核心内部时，杆内只有压应力。Ｄ、当压力作用于截面核心外部时，杆内既有拉应力，又有压应力。组合变形56 3、图示正方形截面直柱，受纵向力P的压缩作用。则当P力作用点由A点移至B点时柱内最大压力的比值有四种答案：（Ａ）１:２（Ｂ）２:５（Ｃ）４:７（Ｄ）５:２组合变形57 4、决定截面核心的因素是。Ａ、材料的力学性质。Ｂ、截面的形状和尺寸。Ｃ、载荷的大小和方向。Ｄ、载荷作用点的位置。组合变形58 组合变形4、图示水平直角折杆受竖直力P作用，轴直径d=100mm，a=400mm，E=200GPa，μ=0.25，在D截面顶点k处测出轴向应变ε=2.75×10-4，求该折杆危险点的相当应力σr3。2PaPa扭矩ADBPa弯矩CDAkaPBaaK点所在截面D的内力：MD=PaT=Pa59 组合变形解:(1)k点应力状态:又(2)危险点：A截面最上边缘点，应力状态与k点相同。k点所在截面D的内力：MD=PaT=Pa60 第八章组合变形及连接部分的计算结束61