北大理论力学课件第四章摩擦.ppt

664.50 KB
19页

北大理论力学课件第四章摩擦.ppt

关闭预览

19页
当前文档由用户上传发布，收益归属用户

下载提示
文本预览

1、本文档共5页，可阅读全部内容。
2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，可选择认领，认领后既往收益都归您。
3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形，可联系本站下载客服投诉处理。
文档侵权举报电话：19940600175。

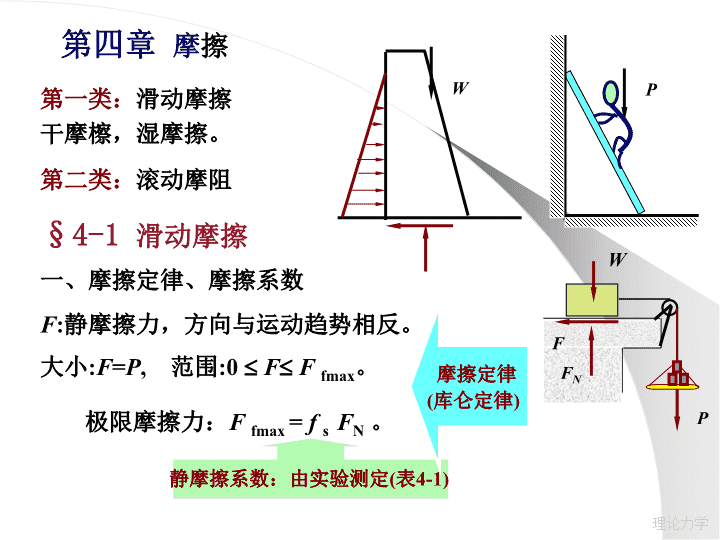
静力学理论力学理论力学第四章摩擦第一类：滑动摩擦干摩檫，湿摩擦。PW第二类：滚动摩阻§4-1滑动摩擦一、摩擦定律、摩擦系数WPFFNF:静摩擦力，方向与运动趋势相反。大小:F=P,范围:0FFfmax。极限摩擦力：Ffmax=fsFN。静摩擦系数：由实验测定(表4-1)摩擦定律(库仑定律)理论力学动摩擦力:Fd=fFN，二、摩擦角Fd思考题2.求：a与摩檫角关系。理论力学思考题3.求：黄沙堆的锥角值a思考题4.求：黄沙输送带的锥角值aa=aaa理论力学例4－1：重量P放在粗糙的斜面上，用力F向上拉，巳知：a>，求：平衡时F力。解：1.不下滑，aPF2FfFNxyFf=fFN，Fix=0,Ff+F1–Psina=0,Fiy=0,FN–Pcosa=0,F1=P(sinafcosa)，2.不上滑，Ff=fFN，Fix=0,–Ff+F2–Psina=0,Fiy=0,FN–Pcosa=0,F2=P(sina+fcosa)，aPFFfFNxyF1FF2。平衡范围1理论力学例4－2：人重为P，不计重量的梯子放在粗糙的地面、墙面上，梯长L,求：平衡时xmin。解：xminFix=0,FBN–FAm=0,Fiy=0,FAN+FBm–P=0,MiB=0,FAmLsina+Pxmin–FANLcosa=0,FBm=fBFBN，FAm=fAFAN，讨论：1.f=fA=fB如:tanm=ctan,90–m。2.fB=0,x2min同上。3.fA=0,x3min=cosL,在A点滑动。4.xmin与P无关。PABaFAmFANFBmFBN理论力学例4－3：活动支架套在固定圆柱上，h=20cm。支架和圆柱之间的静摩擦因数fs=0.25。问x至少多远才能使支架不致下滑（支架自重不计）。hdBAFx取[支架]解:补充方程[解析法]FAFNBFNAABCFxxyhOFB联立求解讨论：x与F无关。理论力学支架受力分析如图所示。由几何关系得解得FDFRBFRAABCxfh1h2f[几何法]解:例4－2A：活动支架套在固定圆柱上，h=20cm。支架和圆柱之间的静摩擦因数fs=0.25。问x至少多远才能使支架不致下滑（支架自重不计）。hdBAFx理论力学例4－4：宽a，高b的矩形柜放置在水平面上，柜重G，重心C在其几何中心，柜与地面间的静摩擦因数是fs，在柜的侧面施加水平向右的力F，求平衡时地面的约束反力，并求能使柜翻倒或滑动所需推力F的最小值。hCabFGABFBFNBFAFNAxy1.假设不翻倒但即将滑动，考虑临界平衡。解:取矩形柜为研究对象,受力分析如图。联立求解得柜子开始滑动所需的最小推力补充方程列平衡方程理论力学 2.假设矩形柜不滑动但将绕B翻倒。柜不绕B翻倒条件：FNA≥0使柜翻倒的最小推力为列平衡方程解得≤hCabFGABFBFNBFAFNAxy理论力学 OABCabcRO1rF1GO1CFfFNFFO1xFO1y[鼓轮]解:解方程得解得得所以[杠杆]AOF1FOxFOyB例4－5：制动器如图所示。制动块与鼓轮表面间的摩擦因数为fs，试求制动鼓轮转动所必需的力F1。理论力学 θⅠⅡⅢⅣ1.取楔块为研究对象，受力分析如图。解：列平衡方程补充方程解方程可得由此得yθOxF1F2FN1FN2例4－6：在坑道支柱施工中的联结结构装置如图所示。它包括顶梁I，楔块II，用于调节高度的螺旋III及底座IV。螺旋杆给楔块以向上的推力FN1。已知楔块与上下支柱间的静摩擦因数均为fs。求楔块不致滑出所需顶角的大小。理论力学将fs=tanφf代入上式得即所以θOxF1F2FN1FN2所以楔块不致滑出的条件为θⅠⅡⅢⅣ例4－6A：在坑道支柱施工中的联结结构装置如图所示。它包括顶梁I，楔块II，用于调节高度的螺旋III及底座IV。螺旋杆给楔块以向上的推力FN1。已知楔块与上下支柱间的静摩擦因数均为fs。求楔块不致滑出所需顶角的大小。理论力学 §4-2滚动摩阻滑动条件：FFm=fFN。FNFmMf滚动摩阻力偶:Mf=FNPrFrFPFNFmFix=0,F–Fm=0,Fiy=0,P–FN=0,MA=0,Fr–Mf=0,滚动摩阻系数,查表4-2.滚动条件：FrMf=FN，先滚后滑A理论力学例4－7：一手拉小车，已知：D=80cm,=0.15cm,Q=1kN,求：拉动时F值。解：[方法一:整体]QFMfFNFmFiy=0,–Q+FN=0,MA=0,FD/2–Mf=0,Mf=FN[方法二:车体]Fx’=F,Fy’=Q，[轮]Fiy=0,Fy–FN=0,MA=0,FxD/2–Mf=0,MfFNFmFXFy[轮]QFFY’FX’[车体]得:得:A理论力学 aCxybθHhFθGAOF1FN1M2f,maxF2FN2M1f,max解：[拖车]FN1FxFyF1M1f,maxOyx[前轮]同样由后轮得临界时的方程解方程可得例4－8：如图所示，总重为G的拖车在牵引力F作用下要爬上倾角为θ的斜坡。设车轮半径为r，轮胎与路面的滚动摩阻系数为δ，其它尺寸如图所示。求拖车所需的牵引力。理论力学解：由得所以所需圈数码头工人船F2F1例4－9：系船的绳索紧绕在码头的立柱上，码头工人以200N的力拉绳索的一端，绳索的另一端拉船的力为7kN，如图所示。已知绳索与立柱之间的静滑动摩擦因数为0.3，问钢索应在立柱绕多少圈才能维持平衡，防止打滑？理论力学本章结束理论力学

北大理论力学课件第四章摩擦.ppt