理论力学课件习题集.ppt

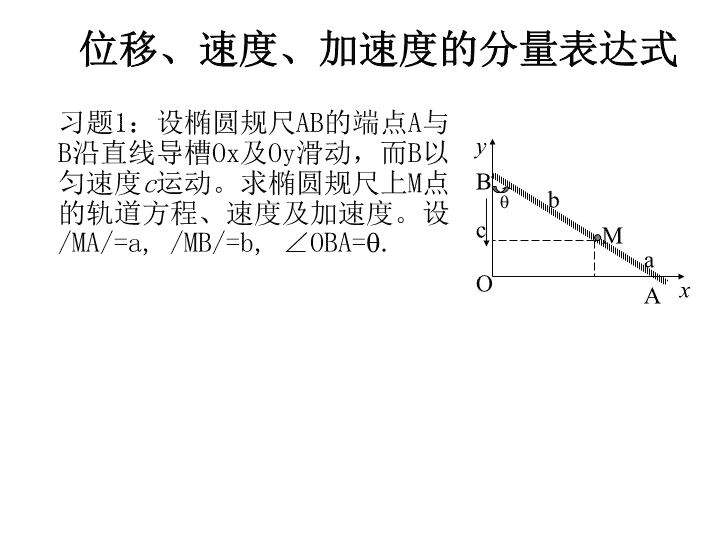
习题1：设椭圆规尺AB的端点A与B沿直线导槽Ox及Oy滑动，而B以匀速度c运动。求椭圆规尺上M点的轨道方程、速度及加速度。设/MA/=a,/MB/=b,∠OBA=.yBcbMaAxO位移、速度、加速度的分量表达式 其方向余弦为：故点Ｍ的加速度大小为选题 习题2证明：在极坐标系中，将加速度a按沿位矢及垂直位矢方向分解为： 习题3某点运动方程为求其速度与加速度（b,c均为常数） 习题4：一质点沿圆滚线切向加速度s=4asinθ的弧线运动，如为一常数，则其加速度亦为一常数。试证明之。式中θ为圆滚线某点P的切线与水平线（x轴）所成的角度，s为P点与曲线最低点之间的曲线弧长。切向加速度习题4，习题5 习题5，设质点P沿螺旋线运动，试求速度、加速度及轨道的曲率半径。 1、圆盘半径为R，以匀角速度绕垂直于盘心O的轴线转动，一质点沿径向槽以匀速度v1向外运动，试求质点加速度各分量的量值。2、在一光滑水平直管中，有一质量为m的小球。此管以恒定角速度绕通过管子一端的竖直轴转动。如果起始时，球距转动轴的距离为a，球相对于管子的速度为0，求小球沿管的运动规律及管对小球的约束反作用力。非惯性系动力学习题 例1椭圆规的曲柄OC可绕定轴O转动，其端点C与规尺AB的中点以较链相接，而规尺A、B两端分别在相互垂直的滑槽中运动，如图所示。已知：OC=AC=BC=l,MC=a,φ=ωt,试求规尺上点Ｍ的运动方程、运动轨迹、速度和加速度。O 解：1）确定M的运动取直角坐标系Ｏxy如图所示2）建立点M的运动方程消去时间t，得轨迹方程点M在BC段上时，椭圆的长轴将与y轴重合。点Ｍ的轨迹是一个椭圆，长轴与x轴重合，短轴与y轴重合O 求点的速度，应将点的坐标对时间取一次导数。得： 其方向余弦为：故点M的速度大小为 求点的加速度，应将点的坐标对时间取二次导数，得： 例题2半径为r的轮子沿着直线轨道无滑动的滚动，设轮子转角为ψ=ωt。求用直角坐标和弧坐标表示轮缘上一点M的运动方程，并求该点的速度、切向加速度、和法向加速度 解：取点M与直线轨道的接触点O为原点.建立直角坐标系Oxy,当轮子转过ψ角时，轮子与直线的接触点为C，因为纯滚动，则直角坐标系表示M点的运动方程为 上式对时间求导，得M点的速度沿着坐标轴的投影 M点的速度大小为M点的速度方向 对速度求导得到直角坐标的加速度投影为M点的加速度方向得M点全加速度 由于:得到： M点运动方程实际是t的参数方程，这是一个摆线方程，表明M点运动为摆线取M的起始点作为弧坐标原点，弧坐标表示的速度方程为：运动方程 法向加速度：由于:得到：返回选题 例3:已知点的运动方程为x=2sin4tm,y=2cos4tm,z=4tm,求点的运动轨迹的曲率半径ρ解：由点的运动方程点的速度沿x,y,z轴的投影分别为：点的速度大小为 点的全加速度的大小为由点的速度方程点的加速度沿x,y,z轴的投影分别为： 点的切向加速度和法向加速度大小为：本题点是运动在半径为2m的圆柱上点的加速度为常量指向轴线选题 例4、小环的质量m，套在一条光滑的钢索上，钢索的方程式为x2=4ay。试求小环自x=2a处自由滑至抛物线顶点时的速度及小环所受到的约束反作用力。x小环在任意位置P处的运动微分方程：yORmgP（1）（2）（1）改写为 质点动力学的基本定理与基本守恒律例5：直所受到的力，如恒通过某一定点，则质点必在一平面上运动，试证明之。 例6：判断作用在质点上的力Fx=x+2y+z+5,Fy=2x+y+z,Fz=x+y+z-6,是否是保守力，并求此质点沿螺旋线x=cos,y=sin,z=7运行自=0=2时，力对质点所做的功。解：1）检验是否保守力：所以作用力是保守力。因为保守力做功与路径无关，所以，求两端点坐标=0，x=1;y=0;z=0=2x=1;y=0;z=14 若Fx=x+2y+z+5,Fy=2x+y+z,Fz=x+y+z-6,，结果如何？