[理学]理论力学课件里所有习题.ppt

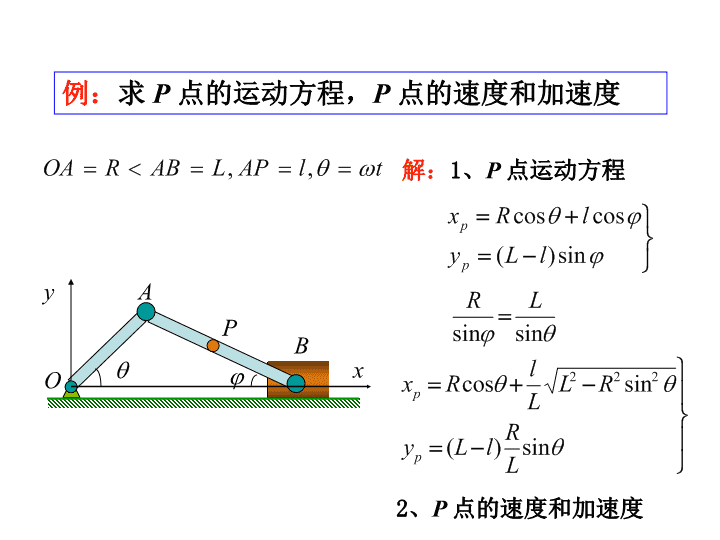
解：1、P点运动方程例：求P点的运动方程，P点的速度和加速度OxyABP2、P点的速度和加速度 列车沿铁轨行驶若将列车视为质点且运动轨迹已知。问题:质点M沿椭圆轨道匀速率运动，如何确定其加速度的大小和方向？问题:如果已知点的运动轨迹和点的速度的大小随时间的变化规律，如何确定点的加速度?过山车车辆转弯时，为什么要限速？高速路坡度拐弯？卫星变轨时从近地轨道转移到远地轨道时，速度的增量是多少？ 例：已知点的运动方程，求点任意时刻的速度、加速度的大小和运动轨迹的曲率半径。运动方程:解： 例：半径为R的车轮在地面上纯滚动，轮心速度的大小为u（常量）。求圆盘与地面接触点的加速度。解：建立M点的运动方程 例：已知图示瞬时动点A的速度和加速度，求该瞬时动点A的。已知：解：A(x,y) 内力的性质对任何一对质点间的相互作用力,由牛顿第三定律知:证明::表示第j个质点对第i个质点的作用力.①质点组中所有内力的矢量和等于零。由于内力是成对出现的第二章 ②质点组的所有内力对任一参考点的力矩的矢量和恒为零.对上式求和就是质点组的所有内力对o点的力矩的矢量和第二章 求半径为R的均质半球的质心。o例题：第二章 ①质点水平方向的加速度;②劈的加速度;③劈对质点的反作用力R1;④水平面对劈的反作用力R2.例：质量为m1的质点，沿倾角为的光滑直角劈滑下，劈的本身质量为m2，又可在光滑水平面上自由滑动。试求第二章 令为沿斜面下滑的速度（相对），则第二章 （非惯性系）对m1有第二章 第二章 例题：雨点开始自由下落时的质量为，在下落过程中，单位时间内凝结在它上面的水汽质量为，略去空气阻力，试求雨点在t秒后所下落的距离。解：因为第二章 积分得：再积分得：第二章 xyzabcO例：求力系｛Fi｝向O点简化的结果。解：1、2、3、根据主矢和主矩的计算结果判断该力系的简化结果。第三章 证明：设三个力不平行且平衡,则：三力共面且作用线交于一点ABCBACABCDABCD若三力平衡，有：由此得：共面因为不平行，相交于D点合成为力由二力平衡原理得：三力作用线共面且交于一点第三章 例：已知AB梁长为l，其上受有均布载荷q，求A处的约束力。AB解：研究AB梁，画受力图。AB第三章 例题一根均匀的棍子，重为P，长为。今将其一端置于粗糙地面上，又一其上的c点靠在墙上，墙离地面的高度为h,当棍子与地面的角度为最小值时，棍子在上述位置仍处于平衡状态，求棍子与地面的摩擦系数。解：是共面力系的平衡问题第三章 解出第三章 例题半径为r的光滑半球形碗，固定在平面上。一均匀棒斜靠在碗缘，一端在碗内，一端在碗外，在碗内的长度为c，试证棒的全长为第三章 解：均质棒受到碗的弹力分别为棒自身重力为。棒与水平方向的夹角为设棒的长度为由于棒处于平衡状态，所以棒沿轴和轴的和外力为零①②第三章 沿过点且与轴平行的合力矩为0。即：③由①②③式得：又由于将⑤代入④得：⑤④第三章 例题：设质量为m的复摆绕通过某点o的水平轴作微小振动，试求其运动方程及其振动周期，并加以讨论。思路:根据转动定律求出振动动力学方程求其运动方程及其振动周期第三章 解运动微分方程由转动方程周期第三章 周期与单摆所具有的形式很类似，所以说单摆是复摆的一个特例。第三章 解选取均匀杆模型进行估算，则自然步频率等于杆的固有频率时（共振）最舒服，如图：Omglθ取l为1米，则步频率为1.62秒例每个人行走时都会有一种自然步频，以这种步频行走很舒服，而试图以较快或较慢的步频行走会感到不舒服。略去膝关节的效应，试用一种最简单的模型来估算该步频。由转动方程第三章 OAB例：已知OA杆的角速度，求图示瞬时滑块B的速度和AB杆的角速度。解：研究AB杆，取A为基点（1）式在AB杆上投影（1）式在OA杆上投影第三章 解：例：曲柄OA以匀角速度转动。求当=60º时，滑块B的速度及连杆AB的角速度。研究连杆AB：（1）速度瞬心可以位于平面运动刚体之上，也可以位于其延展体上。[讨论]第三章 研究连杆AB：（2）当=90º时，滑块B的速度及连杆AB的角速度为多少？P？该瞬时，连杆AB的速度瞬心P在无穷远处，A为基点，杆AB上任一点M的速度该瞬时AB上各点的速度相等。各点加速度是否相等?该瞬时图形上各点的速度分布如同图形作故图形在该瞬时的运动称为瞬时平移。平移时的一样。第三章 例:沿直线轨道作纯滚动的车轮，其半径为R，轮心的速度为u，求轮上A、B、C、D的速度。解：车轮与轨道的接触点A为速度瞬心。车轮的角速度为速度瞬心法的特点：（1）计算简便；（2）直观解了平面运动图形上各点的速度分布。第三章 例题长为的直杆，A端搁在水平地面上，B端靠在墙上，已知A端的水平速度为，求杆与竖直方向成角时B端的速度和杆的角速度。解：瞬心法：方向y轴负方向第三章 基点法求速度第三章 例无滑下滚圆柱体的加速度和约束反力。CO’mgNfOyxC解（A）机械能守恒定律动能势能机械能求微商，得实心圆柱体空心圆柱体不能求约束反力第三章 质心C点的平动方程：绕质心C点的转动方程：联立方程可求得：CO’mgNfOyxC解（B）运动定理第三章 解：这个是一般运动问题[例]当飞机在空中以定值速度V沿半径为R的水平圆形轨道C转弯时，求当螺旋桨尖端B与中心A的联线和沿垂线成θ角时，B点的速度及加速度。已知螺旋桨的长度AB＝l，螺旋桨自身旋转的角速度为ω1。因此，B点的速度为：第三章 B点的加速度为：为恒矢量所以第三章 第三章 AB例：物块A、B放在半径为R处于静止的水平圆盘的边缘，两者间的静滑动摩擦因数为f，物块的质量分别为mA>mB，将物块视为质点，圆盘以角速度ω＝αt绕铅垂轴转动。试确定圆盘转动后，物块开始滑动的时间。gf>αR解：受力分析与运动分析在圆盘面内：t 例在一光滑水平直管中，有一质量为m的小球，此管以恒定角速度ω绕通过管子一端的竖直轴转动。如果起始时，球距转动轴的距离为a，球相对于管子的速度为零，求小球沿管的运动规律及管对小球的约束反作用力。解非惯性参照系小球运动微分方程 ABO二、虚功虚功（virtualwork)：作用于质点(系)上的力在虚位移上所作的功。例：若OA杆的虚位移为，OA＝R，求力F的虚功。 例题：若斜块A和滑块B之间（1）：有摩擦；（2）：无摩擦。则该系统是否是理想约束AB地面光滑（1）：有摩擦是非理想约束（2）：无摩擦是理想约束 例：已知OA=L，求系统在图示位置平衡时，力偶矩M与力F的关系（不计摩擦）ABO基本步骤：确定系统是否满足原理的应用条件分析主动力作用点的虚位移求主动力的虚功之和 BOA AO研究OA杆研究AB杆和滑块BABOAB平衡方程的求解方法 其中：称为对应于的广义力BA例题：套筒A和小球B的重力分别为W1和W2，求系统对应于坐标yA的广义力。 例：求系统的平衡位置。若已知：yxO解：方法一根据独立性 yxO解：方法二yxO 例题半径为r的光滑半球形碗，固定在平面上。一均匀棒斜靠在碗缘，一端在碗内，一端在碗外，在碗内的长度为c，试证棒的全长为解：1个自由度 BByxoA2N1NGqqqq图题1.3.1yxoA2N1Nqqqq 解：均质棒受到碗的弹力分别为棒自身重力为。棒与水平方向的夹角为设棒的长度为由于棒处于平衡状态，所以棒沿轴和轴的和外力为零①② 沿过点且与轴平行的合力矩为0。即：③由①②③式得：又由于将⑤代入④得：⑤④ 平衡的稳定性解：取=0为系统的零势位若：平衡位置是稳定的。例：系统如图所示，滑块的质量为m,杆长为L(不计质量)，当杆铅垂时弹簧无变形，求系统的平衡位置并分析其稳定性。 §5-3达朗贝尔原理动静法例：已知：，求A、B的约束力。解：研究整体,受力分析与运动分析附加动反力：由于运动引起的约束力 §5-3刚体惯性力系的简化1、将惯性力向质心C简化2、将惯性力向转轴A简化3、将惯性力向杆上B点简化AB惯性力向质心C简化：AB惯性力向转轴A简化：思考题：已知均质杆长为L，质量为m，角速度为零，角加速度为，AB惯性力向转轴B简化：如何确定惯性力合力的作用线？ AB动静法的应用例：已知L,m,初始时无初速度，求初始时杆的角加速度和约束力问题：求解该题有几种方法？方法一：动静法解：受力分析、运动分析、添加惯性力建立“平衡”方程求解方程 动静法的应用方法三：应用动能定理和质心运动定理方法二：应用动量矩定理和质心运动定理运动学关系：AB 例：图示系统在铅垂平面内运动，各物体的质量均为m，圆盘的半径为R，圆盘在地面上纯滚动，若板上作用在一个力F。求板的加速度。F应用动力学普遍方程解：运动分析系统自由度k=1受力分析虚位移分析由动力学普遍方程得： ABCABC例：图示系统在铅垂平面内运动，各物体的质量均为m，圆盘的半径为R，绳索与圆盘无相对滑动。求滑块的加速度和圆盘C的角加速度。受力分析解：运动分析应用动力学普遍方程自由度K=2 ABC系统的虚位移动力学普遍方程：ABC 问题：1、系统有几个自由度2、系统的广义坐标是什么3、如何建立运动微分方程4、系统存在哪些守恒量图示机构在铅垂面内运动，均质圆盘在地面上纯滚动，物体间用光滑铰链连接。已知各物体的质量和几何量。ABC 例题质点在主动力F的作用下作平面曲线运动，求其平面极坐标下动力学方程表达式。解： 令则令则令 代入基本形式的拉格郎日方程 例求质点在单摆中的动力学方程广义坐标为S=1 代入动力学方程 例求质点在重力场中的动力学方程广义坐标为x,y.zS=3 代入 例求质点在重力场中的运动广义坐标为x,y.zS=3 拉氏函数不显含循环坐标物理含义：抛体运动中，x，y方向动量守恒。 2.如图所示，轴为竖直而顶点在下的抛物线金属丝，以匀角速绕轴转动，一质量为的小环，套在此金属丝上，并可沿着金属丝滑动，试用分析力学的方法求出小环在方向的运动微分方程。已知抛物线的方程为，式中为一常数。yxo图4（第六题） 自由度是1解：yxo图4（第六题）根据转动参照系速度关系可以写出因而质点相对于静止坐标系的动能是 -代入保守系的拉格朗日方程得 3如图所示，有一质量为m的单摆B，摆长为，摆悬挂在质量为M的滑块A上，滑动可在一光滑直线轨道上运动。 +代入拉格朗日方程所以x为循环坐标水平方向上动量守恒 4.质量为m1的质点被限制在固定的光滑直线上滑动，另一质量为m2的质点，以一长度为的无质量杆和m1相连，设杆仅在通过固定直线的竖直平面内运动，且二质点仅受重力作用。 m1m2 选择轴所在平面为零时能参考点X为循环坐标X方向动量守恒