哈工大理论力学课件第09章

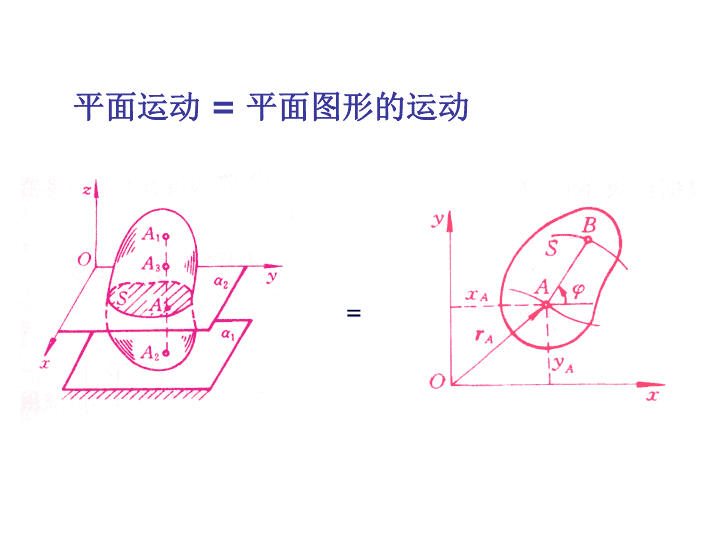
第九章刚体的平面运动 §9-1刚体平面运动的概述和运动分解1、平面运动在运动中，刚体上的任意一点与某一固定平面始终保持相等的距离，这种运动称为平面运动。 平面运动=平面图形的运动= 广义坐标运动方程基点速度角速度2、运动方程 3、运动分解=+平面运动=随　的平移+绕　点的转动平移坐标系 §9-2求平面图形内各点速度的基点法1.基点法速度公式 2、基于运动分解的基点法速度公式动点：M绝对运动：待求牵连运动：平移动系：(平移坐标系)相对运动：绕点的圆周运动 任意A，B两点平面图形内任一点的速度等于基点的速度与该点随图形绕基点转动速度的矢量和。其中大小方向垂直于，指向同 例9-1椭圆规尺的A端以速度vA沿x轴的负向运动，如图所示，AB=l。求：B端的速度以及尺AB的角速度。 解：1、AB作平面运动，基点：A 例9-2如图所示平面机构中，AB=BD=DE=l=300mm。在图示位置时，BD∥AE，杆AB的角速度为ω=5rad/s。求：此瞬时杆DE的角速度和杆BD中点C的速度。 解：1、BD作平面运动基点：B 例9-3曲柄连杆机构如图所示，OA=r,AB=。如曲柄OA以匀角速度ω转动。求：当时点的速度。 解：1、AB作平面运动基点：A0Bv=0j=o 例9-4如图所示的行星轮系中，大齿轮Ⅰ固定，半径为r1，行星齿轮Ⅱ沿轮Ⅰ只滚而不滑动，半径为r2。系杆OA角速度为。求：轮Ⅱ的角速度ωⅡ及其上B，C两点的速度。 解:1、轮Ⅱ作平面运动基点：A３、 练习9-1已知求:vC 解：1.AB杆作平面运动，A=基点 2. 3、速度投影定理同一平面图形上任意两点的速度在这两点连线上的投影相等。沿AB连线方向上投影由 例9-5如图所示的平面机构中，曲柄OA长100mm，以角速度ω=2rad/s转动。连杆AB带动摇杆CD，并拖动轮E沿水平面纯滚动。已知：CD=3CB，图示位置时A，B，E三点恰在一水平线上，且CD⊥ED,OA⊥AB求：此瞬时点E的速度。 解：1、AB作平面运动2、CD作定轴转动，转动轴：C3、DE作平面运动 杆AB的A端沿水平线以等速v运动，运动时杆恒与一半圆周相切，半圆周的半径为R，如图所示。如杆与水平线间的交角为θ，试以角θ表示杆的角速度。 四连杆机构中，连杆AB上固连一块三角板ABD，如图所示。机构由曲柄O1A带动。已知：曲柄的角速度ωOA=2rad/s；曲柄O1A=0.1m，水平距离O1O2=0.05m，AD=0.05m；当O1A铅直时，AB平行于O1O2，且AD与O1A在同一直线上；角φ=30º。求点D的速度。 §9-3求平面图形内各点的瞬心法一般情况下,在每一瞬时,平面图形上都唯一地存在一个速度为零的点，称为瞬时速度中心，简称速度瞬心。1、定理基点：A 平面图形内任意点的速度等于该点随图形绕瞬时速度中心转动的速度。基点：C2、平面图形内各点的速度分布 3、速度瞬心的确定方法已知的方向，且不平行于。 瞬时平移(瞬心在无穷远处)且不垂直于纯滚动(只滚不滑)约束 运动方程 ODCBAvOC速度分布 例9-6椭圆规尺的A端以速度vA沿x轴的负向运动，如图所示，AB=l。求：用瞬心法求B端的速度以及尺AB的角速度。 解：AB作平面运动，速度瞬心为点C。 例9-7矿石轧碎机的活动夹板AB长600mm，由曲柄OE借连杆组带动，使它绕A轴摆动，如图所示。曲柄OE长100mm，角速度为10rad/s。连杆组由杆BG，GD和GE组成，杆BG和GD各长500mm。求：当机构在图示位置时，夹板AB的角速度。 解:1、杆GE作平面运动，瞬心为C1。2、杆BG作平面运动，瞬心为C。 图示机构中，已知：OA=0.1m，BD=0.1m，DE=0.1m，EF=0.1m；ωOA=4rad/s。在图示位置时，曲柄OA与水平线OB垂直；且B、D和F在同一铅直线上。又DE垂直于EF。求杆EF的角速度和点F的速度。 §9-4用基点法求平面图形内各点的加速度平面图形内任一点的加速度等于基点的加速度与该点随图形绕基点转动的切向加速度和法向加速度的矢量和。基点：A平移坐标系：大小方向垂直于，指向同大小方向由指向 例9-8如图所示，在椭圆规机构中，曲柄OD以匀角速度ω绕O轴转动。OD＝AD＝BD＝l。求：当时，尺AB的角加速度和点A的加速度。 解：1、AB作平面运动，瞬心为C。 例9-9如图所示，在外啮合行星齿轮机构中，系杆以匀角速度ω1绕O1转动。大齿轮固定，行星轮半径为r，在大轮上只滚不滑。设A和B是行星轮缘上的两点，点A在O1O的延长线上，而点B在垂直于O1O的半径上。求：点A和B的加速度。 解:1、轮Ⅰ作平面运动，瞬心为C。2、选Ｏ为基点√√√ √√√ 求：车轮上速度瞬心的加速度。例9-10车轮沿直线滚动。已知车轮半径为R，中心O的速度为，加速度为，车轮与地面接触无相对滑动。 解：1、车轮作平面运动，瞬心为C。3、选Ｏ为基点 半径为r的圆柱形滚子沿半径为R的圆弧槽纯滚动。在图示瞬时，滚子中心C的速度为vC、切向加速度为act。求这时接触点A和同一直径上最高点B的加速度。 曲柄OA以恒定的角速度ω=2rad/s绕轴O转动，并借助连杆AB驱动半径为r的轮子在半径为R的圆弧槽中作无滑动的滚动。设OA=AB=R=2r=1m，求图示瞬时点B和点C的速度与加速度。 §9-5运动学综合应用举例1、运动学综合应用：机构运动学分析。2、已知运动机构未知运动机构3、连接点运动学分析接触滑动—合成运动铰链连接—平面运动 求：该瞬时杆OA的角速度与角加速度。例9-11图示平面机构，滑块B可沿杆OA滑动。杆BE与BD分别与滑块B铰接，BD杆可沿水平轨道运动。滑块E以匀速v沿铅直导轨向上运动，杆BE长为。图示瞬时杆OA铅直，且与杆BE夹角为 解：1、杆BE作平面运动，瞬心在O点。取E为基点沿BE方向投影 绝对运动：直线运动(BD)相对运动：直线运动(OA)牵连运动：定轴转动(轴O)2、动点：滑块B动系：OA杆√√√沿BD方向投影 沿BD方向投影 求：此瞬时杆AB的角速度及角加速度。例9-12在图所示平面机构中，杆AC在导轨中以匀速v平移，通过铰链A带动杆AB沿导套O运动，导套O与杆AC距离为l。图示瞬时杆AB与杆AC夹角为。 解：1、动点：铰链A动系：套筒O 另解：1、取坐标系Oxy2、A点的运动方程3、速度、加速度 求：此瞬时AB杆的角速度及角加速度。例9-13如图所示平面机构，AB长为l，滑块A可沿摇杆OC的长槽滑动。摇杆OC以匀角速度ω绕轴O转动，滑块B以匀速　　　　沿水平导轨滑动。图示瞬时OC铅直，AB与水平线OB夹角为。 2、动点：滑块A，动系：OC杆1、杆AB作平面运动，基点为B。√√√√沿方向投影解：速度分析 √√√√√√√加速度分析 例9-14如图所示平面机构中，杆AC铅直运动，杆BD水平运动，A为铰链，滑块B可沿槽杆AE中的直槽滑动。图示瞬时求：该瞬时槽杆AE的角速度、角加速度及滑块B相对AE的加速度。 解：动点：滑块B动系：杆AE基点：A 沿方向投影沿方向投影