北大理论力学课件第三章空间力系

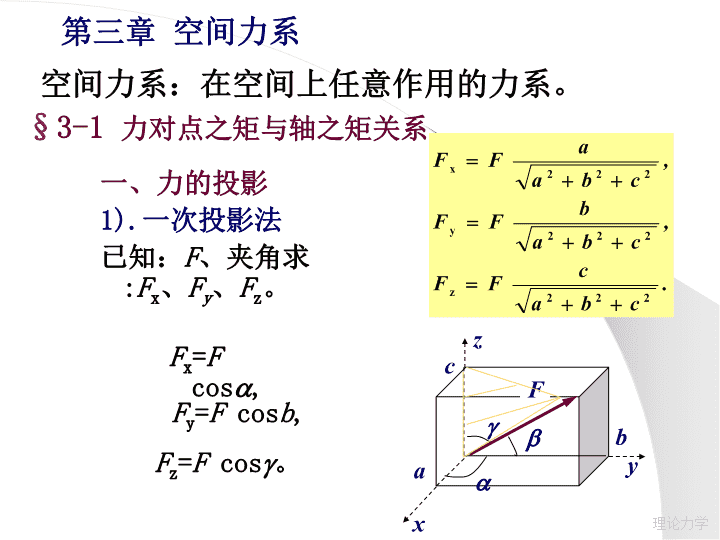
静力学理论力学理论力学 一、力的投影1).一次投影法已知：F、夹角求:Fx、Fy、Fz。Fx=Fcosa,xyzagbFcabFy=Fcosb,Fz=Fcosg。第三章空间力系空间力系：在空间上任意作用的力系。§3-1力对点之矩与轴之矩关系理论力学 2).合成已知：Fx、Fy、Fz，求F、夹角。Fx=Fxycosq=FsingcosqFy=FsingsinqFz=Fcong3).二次投影法已知：F、夹角q，g,求：Fx、Fy、Fz。FFxygqxy`zFxy=Fsing理论力学 FRx=Fix,FRy=Fiy,FRz=Fiz,F3FRFR2F2F4FR1F1F2F1F4F3xy`zFR4)、合力投影定理ijk力的矢量分解式理论力学 例3-1:巳知:F1=3kN,F2=2kN,求合力值。解：xy`zF1F2354理论力学 FrFxyMzzM0gMx=(yFz-zFy)，Mz=(xFy-yFx)My=(zFx-xFz)，Mz=M0cosg力对轴之矩(代)与力对点之矩(矢)关糸右手法则为正二、力对点之矩与轴之矩关系理论力学 合力矩定理My=Miy，Mz=Miz，Mx=M1x+M2x+M3x=Mix，合力对点(或轴)之矩等于各分力对同点(或轴)之矩的矢量和(代数和)。理论力学 xyzFba0AB例3-2：拖拉机摇手柄OAB在oxz平面内，在A处作用一个力F,已知：F=50N,0A=20cm,AB=18cm,a=450,b=600,求各轴之矩。解：Fx=Fcosbcosa=17.7NFy=Fcosbsina=17.7NFz=Fsinb=43.3NMx=18·43.3-20·17.7=426N·mMy=20·17.7=354N·mMz=–18·17.7=-318N·mMx=(yFz-zFy)，Mz=(xFy-yFx)My=(zFx-xFz)，x=0,y=18,z=20,理论力学 三、空间力偶AF’FrABBM右手法则为正1).任意搬动(水平、垂直)2).力偶矩矢5105=10大小、转向F’FM等效条件kN·m理论力学 一、简化F2A2AnFNzxy0zxy0M1F1F1A1FRM2F2FnMnzxy0M0简化中心附加力偶主矢：主矩：主矢，主矩§3-2简化与平衡理论力学 FRx=Fix，FRy=Fiy，FRz=Fiz，合力矩投影定律Mx=Mix，My=Miy，Mz=Miz，合力投影定律主矢：主矩：理论力学 讨论:1、FR=0，M0≠0；一个力偶；2、FR≠0，M0=0；一个力；3、FR=0，M0=0，（平衡）；4、FR≠0，M0≠0；=FR’FR”00’FR(1)FRaM0FR(2)FRM‖M(3)M0(1).M0FR；FR=FR’=FR”，(2).M0‖FR；(3).M0，FR；M‖FRM000’=a=M0/FR”；右手力螺旋；右手力螺旋。一个力等效条件任意搬动(水平、垂直)理论力学 二、平衡Fix=0，Fiy=0，Fiz=0，Mix=0，Miy=0，Miz=0，空间任意物体具有六个平衡方程可解六个未知量。理论力学 空间汇交力系平衡方程空间力偶力系平衡方程Fix=0，Fiy=0，Fiz=0，Mix=0，Miy=0，Miz=0，空间平行力系平衡方程Fiz=0，Mix=0，Miy=0，具有三个平衡方程可解三个未知量。理论力学 例3－3：重量P=1kN，A是球铰支座、A、B、C点是固定在同一墙上，求：杆AD、绳DB，DC的约束内力。解：这是空间汇交力系，取D点为汇交点，BE=CE,DB=DC,则：FDB=FDCFDB=FDC=289N。FDCFDAFDBP[D]理论力学 xyzPCBE450AD450300450450450例3－4：起重机起吊重量P=1kN，求：立柱AB、绳BC，BD，BE的拉力。解：B点有四个未知力汇交，故先从C点求解，[C]平面汇交力系Fix’=0,FCBsin300一Psin450=0,FCB=1.414P，理论力学 xyzPCBE450AD450300450450450例3－4A：起重机起吊重量P=1kN，求：立柱AB、绳BC，BD，BE的拉力。解：B点有四个未知力汇交，x’FCAFCB450P750FBEFBDFBAFBC[B]空间汇交力系Fix=0,FBDcos2450一FBEsin2450=0,FBD=FBEFiy=0,–2FBDcos450sin450+FBCsin750=0,Fiz=0,–2FBDsin450–FBA+FBCcos750=0,FBA=–1.564P。柱AB受压。理论力学 例3－5：三叉杆件上作用已知力偶M1=5N·m，为平衡杆件在杆上作用约束力偶M2、M3，求：约束力偶值。解:这空间力偶系，因力偶在0yz平面，MX0，300M1zyM2M3My=0,M1+M3sin300=0,M3=–10N·m,Mz=0,M2+M3cos300=0,理论力学 例3－6：工件如图所示，它的四个面上同时钻五个孔，每个孔所受的切削力偶矩均为80N·m。求工件所受合力偶的矩在x，y，z轴上的投影Mx，My，Mz，并求合力偶矩矢的大小和方向。将作用在四个面上的力偶用力偶矩矢表示，并平移到A点。可得所以合力偶矩矢的大小合力偶矩矢的方向余弦解：理论力学 例3－7：三轮平板车放光滑地面上，自重为：W，货重为F，已知：F=10kN,W=8kN,求：各轮约束反力值。解：这是空间平行力系，六个平衡方程仅有三个独立的，而Fix0，Fiy0，MZi0，FAFBFCFiz=0，xyzMix=0,(200–80)W–200·FA=0；FA=4.8kN，FA+FB+FC–W–F=0；Miy=0，60W+(60–20)F–60·FA–2·60·FB=0；FB=4.93kN，FC=8.27kN；理论力学 例3－8：直角三棱柱上有作用力：F1=200N,F2=F’2=100N，求：所有力对各轴投影值与力矩值。M2解：空间力偶矢M2=F2·0.2=100N·mMx=(yFz–zFy)=–0.4·111.41–0=–44.56N·m理论力学 例3－9：均质矩形板重P=200N,板用球形铰链A、蝶形铰B与绳CE固定在墙上，若=300，求：所有约束力值。FAX=86.6N,解：这是空间力系，有六个平衡方程FBXFBZPxyzFAZFAXFAYMiz=0,FBX=0,Miy=0,Mix=0,FBZ=0Fix=0,FAX+FBX–Fcos300cos600=0,Fiy=0,FAY–Fcos2300=0,FAY=150N,Fiz=0,FBZ+FAZ–P+Fsin300=0,FAZ=100N,校核:MDB=0。FF=200N理论力学 例3－10：水平圆盘绕AB转轴，A点为轴承，B点止推轴承，已知：P=100kN，r1=0.2m,r2=0.5m,a=1m,=300，=600，求：平衡时F力与所有约束力值FAYFAxFBxFByFBzyxzP解：F力是任意力，可分解成Mix=0,–3aFAy+2aP+aFy–r2cos300Fz=0;FAy=63.6kN,Miy=0,3aFAx+aFx+r2cos600Fz=0;FAx=–7.32kN,Fx=Fcos600cos300=34.64kN,Fy=Fcos2600=20kN,Fz=–Fsin600=69.28kN,Miz=0,Pr1–Fcos600r2=0;F=80kN;理论力学 Fix=0,FAx+FBx+Fx=0;Fiy=0,FAy+FBy–Fy–P=0;FAYFAxFBxFByFBzyxzPFBx=–17.32kN;FBy=56.6kN;Fiz=0,–FBz+Fz=0;FBz=69.28kN;理论力学 解：Miz=0,Pr1–Fcos600r2=0;F=80kN;Fx=Fcos600cos300=34.64kN,Fy=Fcos2600=–20kN,Fz=–Fsin600=–69.28kN,FAy=63.6kN,Miy=0,3aFAx+aFx+r2cos600Fz=0;Mix=0,–3aFAy+2aP+aFy–r2cos300FZ=0;Fix=0,FAx+FBx+Fx=0;Fiy=0,FAy+FBy–Fy–P=0;FBx=–17.32kN;FBy=56.6kN;Fiz=0,–FBz+Fz=0;FBz=69.28kN;FAyFAxFBxFByFBzyxzPFAx=–7.32kN,理论力学 三力矩平衡方程:Mix=0，Miy=0，Miz=0，Fix=0，Fiy=0，Fiz=0，四力矩平衡方程:Mix=0，Miy=0，Miz=0，Fix=0，Fiy=0，MAB=0，五力矩平衡方程:Mix=0，Miy=0，Miz=0，Fix=0，MBC=0，MAB=0，六力矩平衡方程:Mix=0，Miy=0，Miz=0，MCD=0，MBC=0，MAB=0，每个空间平衡物体仅六个独立平衡方程，证明其独立条件很困难，但一个方程中仅一个未知量，这个方程是独立方程。理论力学 例3－11：边长为a的等边三角形水平板上作用着力偶M，並用六根二力杆支撑，板自重不计，求：各杆的内力。解:F1F3F6F4F5F2MAD=0,F5cos300a·cos300+M=0;MFB=0,F6cos300a·cos300+M=0;`MEC=0,F4cos300a·cos300+M=0;MCA=0,–F5a·sin600–F2sin300a·sin600=0;MAB=0,–F3a·sin600–F6sin300a·sin600=0;MBC=0,–F1a·sin600–F4sin300a·sin600=0;理论力学 例3－12：长度相等、互为直角的AB、CD杆在中点E以铰链连接，並在D端悬挂重物P=25kN，求：各约束反力。解:Fix=0,FAx+FCx=0;（1）Fiy=0,FAy+FCy–Fcos450=0;（2）Fiz=0,FAZ+FCZ+Fsin450=25;（3）Mx=0,Fsin450·AD–P·AD=0;（4）My=0,–FAz·AC+P·AC=0;（5）Mz=0,FAy=0;（6）六个方程有七个未知量，应一个补充方程。FAyFAZFAXFCXFCyFCZF理论力学 [CD]用有关的简单物体分析；联立求解这7个方程，可解得：FAx=–25kN，FCx=25kN，FAy=0,FCy=25kN，FAx=25kN，FCx=–25kN，F=35.5kN。FAyFFAZFAXFCXFCyFCZMz‘=0,FCxCE·sin450–FCy·CEcos450=0;（7）理论力学 §3-3重心My=0,Pxc=PixirirCPi(xi,yi,zi)P(xc,yc,zc)ycxcyxzyixiMx=0,Pzc=PiziMx=0,Pyc=Piyi绕x转90度,有：理论力学 均质物块：P=U,(比重×体积U)xc=Uixi/Uyc=Uiyi/Uzc=Uizi/U均质板壳：P=At,(比重×面积A×t厚度)xc=Aixi/Ayc=Aiyi/Azc=Aizi/A均质梁杆：P=LA,(比重×长度L×截面积A)xc=Lixi/Lyc=Liyi/Lzc=Lizi/LLAU积分法积分法积分法理论力学 例3－13：图示均质扇形薄板，求：重心的位置。解：取对称轴故yc=0，再用极坐标示积分式。xyC如：=/2，则:xc=(4r/3)积分法rxydSd理论力学 例3－14：图示槽钢横截面，求：此截面重心的位置。A1=30•10=300cm2,x1=15cm；解：取对称轴故yc=0，再分割成有规律的几个物体，A2=20•10=200cm2,x2=5cm；A3=30•10=300cm2,x3=15cm；分割法：将物体分割成有规律的几个物体，理论力学 例3－15：图示为机械振动打桩机偏心块，巳知：R=10cm,r=1.7cm,b=1.3cm，求：此重心的位置。解：取对称轴故xc=0，再分割成A1,A2,A3三个物体，A3A1A2yx负面积法理论力学 例3－16：用负面积法求第11题槽钢横截面重心的位置。解：再分割成二块有规律的矩形物体，A1是正面积，A2是负面积，代入公式结果同前。A1A2理论力学 例3－17：图示为任意板块物体，试用试验法板块求重心的位置。解：`PA`PCB1.先在物体A点悬挂作垂直线；2.再在物体B点悬挂作垂直线；3.二根垂直线交点C是重心的位置。悬挂法理论力学 例3－18：图示为一辆轿车，试用试验法求轿车重心的位置。1.轿车平放用称重法求xC；ABCPLxCFNAFNB解：MB=0,FNAL=Pxc；xC=FNAL/P。2.轿车后轮抬高,用称重法求ZC；MB=0,FNA‘L‘=Pxc’；xC‘=FNA‘L’/P。有：L’=Lcosa,x’C=xCcosa+hsina；h=zC–r代入上式整理后有：称重法BCPL’xc’F‘NAF’NBAZCah理论力学 本章结束理论力学