理论力学课件 动量矩定理

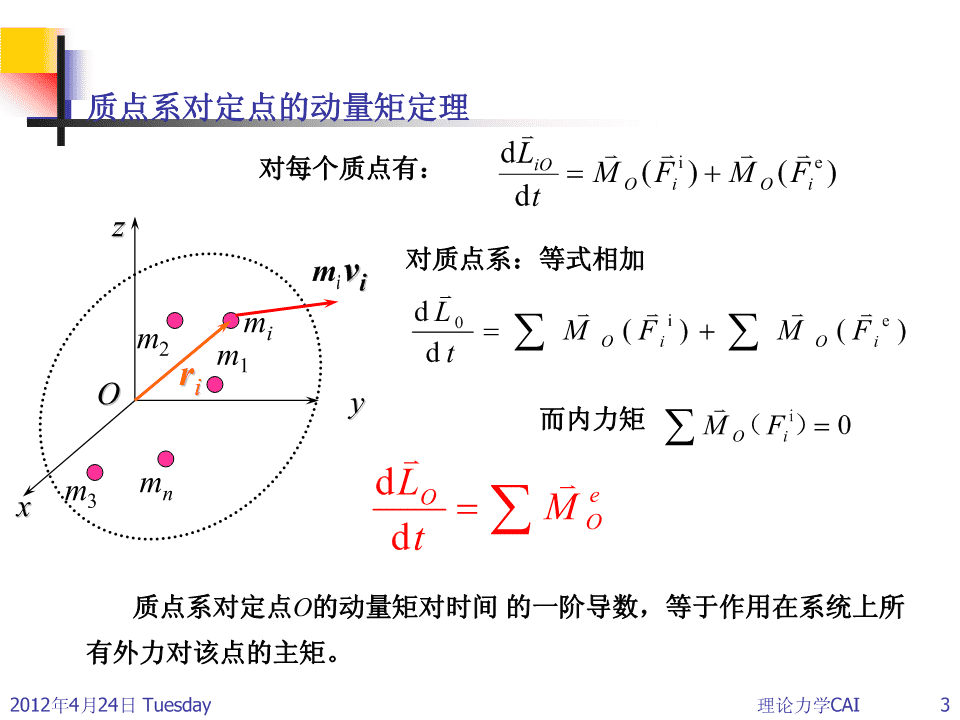
第12章动量矩定理研究质点系转动与外力矩之间的关系2012年4月24日Tuesday理论力学CAI1 §12.1质点系动量矩定理mv1.质点系的动量矩定理r质点的动量矩Mmvrmvo质点的动量矩求导OdM(mv)drdOmvr(mv)rFM(F)Odtdtdt质点对定点的动量矩定理：d[M(mv)]M(F)OOdt质点对固定点O的动量矩对时间的导数，等于作用在质点上的力对O点之矩。这就是质点对固定点的动量矩定理。2012年4月24日Tuesday理论力学CAI2 质点系对定点的动量矩定理dLiOie对每个质点有：M(F)M(F)OiOidtzm对质点系：等式相加ivvimdL0iemiMO(Fi)MO(Fi)2mdt1rriOy而内力矩M（Fi）0Oim3mndLOexMOdt质点系对定点O的动量矩对时间的一阶导数，等于作用在系统上所有外力对该点的主矩。2012年4月24日Tuesday理论力学CAI3 质点系动量矩定理的投影形式在直角坐标轴上投影dLxeMxFidtdLyeMyFi对定轴的动量矩dtdLzeMFzidt质点系对于定轴的动量矩对时间的一阶导数等于作用在系统上所有外力对同一轴取矩的代数和。2012年4月24日Tuesday理论力学CAI4 动量矩守恒定律若MoF0则L0常矢量投影形式若MzF0则L常数z2012年4月24日Tuesday理论力学CAI5 2.动量矩的计算1）对质心的绝对动量矩和相对动量矩对质心C的绝对动量矩绝对速度vvvmvLρmviCirCiiiρimivCvir(miρi)vCρimivirrLC对质心C的相对动量矩rLCρimivir质点系对质心的绝对动量矩和相对动量矩相等。rLLCC2012年4月24日Tuesday理论力学CAI6 2）质点系对任意定点O的动量矩的一个实用计算LOMO(mivi)rimivi质点的绝对位矢rrρiCiLO(rCi)(mivi)rCmiviimivivvv绝对速度iCir质心mvmviiCLOrCmvC(imivC)(imivir)rCmvC(mii)vC(imivir)rrrmvmrvLCCCCCrrmvLCCC2012年4月24日Tuesday理论力学CAI7 质点系对任意定点O的动量矩质点系对任意定点O的动量矩等于集中于质心的动量mv对O点的动量矩再加上各质点相对质心C动量矩L的矢量和。CrLrmvLOCCC2012年4月24日Tuesday理论力学CAI8 3）刚体的动量矩计算①平移刚体的动量矩LO(rimivi)mirivCrCmvCmirimrC对定点的Lm(mv)rmvOOCCC对定轴的LM(mv)zzC平移刚体对固定点（轴）的动量矩等于刚体质心的动量对该点（轴）的动量矩。2012年4月24日Tuesday理论力学CAI9 ②定轴转动刚体对转轴的动量矩LzMzmivimiviρi22miωρiωmiρi2Jzmii称为刚体对z轴的，转动惯量转动惯量是刚体转动惯性的度量。2Jmz称为惯性半径zz刚体对定轴z的动量矩可写成：LJzz2012年4月24日Tuesday理论力学CAI10 ③平面运动刚体平面运动刚体对质心的动量矩刚体对质心的绝对动量矩和相对动量矩相等。r2LCLCρimiωρimiρiωrLLJCCC刚体对任意定点O的动量矩LMmvJOOCC平面运动刚体对任意定点O的动量矩LM(mv)JOOCC2012年4月24日Tuesday理论力学CAI11 练习：求图示匀质物体对固定点的动量矩。OOORCCllOl/32012年4月24日Tuesday理论力学CAI12 练习：求系统动量矩图示系统中，已知鼓轮以ω的角速度绕O轴转动，其大、小半径分别为R、r，对O轴的转动惯量为JO；物块A、B的质量分别为mA和mB；试求系统对O轴的动量矩。ωOrRBAθ2012年4月24日Tuesday理论力学CAI13 §12.2刚体绕定轴转动微分方程定轴转动刚体的动量矩：LJzz刚体对z轴的动量矩定理dLd由zMzFiJzMzFidtdt刚体绕定轴转动微分方程JZMzFidJZMzFidt,,d2JZMzFi2dt2012年4月24日Tuesday理论力学CAI14 例12-2两个质量为m、m的重物分别系在绳子的两端，如图所示。两绳分12别绕在半径为r1、r2并固结在一起的两鼓轮上，设两鼓轮对O轴的转动惯量为JO，重为W，求鼓轮的角加速度和轴承的约束力。解：（1）以整个系统为研究对象。（2）受力分析：系统所受外力的受力图如图所示，其中mg、mg、12W为主动力，F，F为约束力。xy（3）运动分析：设鼓轮的角速度为，系统的动量矩为22L(Jmrmr)OO1122（4）应用动量矩定理dLOM(F)Odt22(Jmrmr)mgrmgrO112211222012年4月24日Tuesday理论力学CAI15 得到鼓轮的角加速度为mrmr1122g22JmrmrO1122（5）应用动量定理mxFxmyFy0FxmrmrFmgmgW1122y12得到轴承约束力为F0x2(mrmr)F（mm）gW1122gy1222JmrmrO11222012年4月24日Tuesday理论力学CAI16 例动量矩守恒物块重W，人重W，保持平衡。人从静止开始，以相对绳速度v向上运动，问平衡块将怎样运动？（轮重不计）r设物块上升的速度v对O点的动量矩守恒WWvR(vv)R0rgg1vvr22012年4月24日Tuesday理论力学CAI17 例12-1在光滑水平面上放置半径为R的圆环，在环上有一个质量与环相同的小虫，以相对环的等速率v爬行。设开始时环与虫都静止。求环的角速度。解：取环和小虫组成的系统研究。其受到的合外力为零，系统的质心C守恒，系统对质心C的动量矩守恒设系统质心位置为C，则OC=CA=0.5R环与小虫的质量均为m，假定环运动的角速度为ω（逆时针）。Rω小虫的绝对速度：v虫vACωv2系统对质心C的动量矩守恒LJm(vR/)2ACCC222mRm(R/)2mRv/2m(R/)20v解得：负号表示圆环转向与所设相反，为顺时针3R2012年4月24日Tuesday理论力学CAI18 例题12-4刚体定轴转动均质杆OA，重P，长l，绳子突然剪断。求该瞬时，OA杆角加速度及O处反力。解：取杆为研究对象，由动量矩定理：1P2l3glP3g22l由质心运动定理：Pa0FCxOxgPPl1aFPFPCyOyOygg242012年4月24日Tuesday理论力学CAI19 例12-3复摆法测转动惯量水平轴为摆的悬挂轴。设摆的质量为m，质心为C，s为质心到悬挂轴的距离。若已测得复摆绕其平衡位置摆动的周期T，求刚体对通过质心并平行于悬挂轴的轴的转动惯量。解：根据对固定点的动量矩定理有JmgssinOJ——对O轴的转omgs动惯量sin0JOmgs微幅摆动sin近似微分方程0JO2mgsJ2解得周期OTmgsT2JJOmgsO242由平行轴定理JOJCms22Ts对质心的转动惯量JCJOmsmgs(2)4g2012年4月24日Tuesday理论力学CAI20 §12.3刚体平面运动微分方程1.质点系相对质心的动量矩定理zmmidLC(e)z02mMC1dtCiyxiCmmnO3y在相对随质心平动坐标系的运动中，质00点系对质心的动量矩对于时间的一阶导数等于外力系对质心的主矩。02012年4月24日Tuesday理论力学CAI21 2.刚体平面运动微分方程maFcxxmaFcyyeJM(F)CCi或mxFCxmyFCyJMczcz2012年4月24日Tuesday理论力学CAI22 例12-5均质圆盘质量为m，半径为R，对质心的回转半径为。试研C究圆盘沿倾斜角为θ的斜面的平面运动。不计滚动摩阻。解：(情况1)斜面为光滑斜面。圆盘的受力如图由刚体平面运动微分方程得出mxmgsinC0FmgcosN2m0Cxgsin由此可得到各运动分量满足方程C0若初始条件为t,0xv,x,0,00C0Cxgsin则圆盘以加速度C作平移运动若初始条件为t,0x,0x,0,0圆盘平面运动CC2012年4月24日Tuesday理论力学CAI23 情况2斜面有足够粗糙度（圆盘不打滑）圆盘受力如图刚体平面运动方程mxmgsinFC0FmgcosN2mFRC圆盘不打滑，为纯滚动，运动有约束方程xCRxRxCRC2R圆盘与斜面间无相对滑动的条件为解得xgsinC22RCFfF2NCFmgsin22RC圆盘沿斜面作纯滚动的条件为摩擦系数Fmgcos2NCftan22RC2012年4月24日Tuesday理论力学CAI24 情况32C圆盘与斜面间的摩擦系数0ftan22RC圆盘沿斜面既滚又滑，具有两个自由度，选x、为广义坐标CmxmgsinθFC0FmgcosθN2mρFRC动滑动摩擦力FfFNfmgcos解得x(sinfcos)gCRfgcos2C圆盘质心的加速度与圆盘重量无关，只与动滑动摩擦系数有关。2012年4月24日Tuesday理论力学CAI25 解：取系统为研究对象，应用对固定点A的动量矩定理dJmvrmgrCCdtaC12Jmarmgr,JmrCCCr22agC3质心运动定理mamgFC1FmgmamgC32012年4月24日Tuesday理论力学CAI26 求运动微分方程解：以为圆柱研究对象，在任意位置tn2质心加速度aRr,aRrCCmRrFmgsin质心运动微分方程：2mRrFmgcosP为瞬心N质心速度vCRrrtvRraRrCC圆柱的角速度及叫加速度rrrr2对质心的动量矩定理mrRr圆柱的运动微分方程：Fr2r2gsin03Rr2012年4月24日Tuesday理论力学CAI27 练习：图示系统中，已知鼓轮绕O轴转动，其大、小半径分别为R、r，对O轴的转动惯量为JO；物块A、B的质量分别为mA和mB，斜面光滑。试求物块A下降的加速度。ωOrRBAθ2012年4月24日Tuesday理论力学CAI28 本章小结：dLOe刚体系对定点的动量矩定理MOdtdLC对质心的动量矩定理MCdt刚体的定轴转动微分方程JZMz刚体平面运动微分方程macxFxmacyFyJCMC质点系的动量矩定理反映了质点系转动的规律与外力矩之间的关系。只有外力矩才能改变质点系的转动状态，内力矩不能改变质点系的转动状态。对于定轴转动刚体，质点系的动量矩定理就是刚体的定轴转动微分方程。2012年4月24日Tuesday理论力学CAI29 课后作业1作业题12-212-312-42012年4月24日Tuesday理论力学CAI30 课后作业2作业题12-612-712-92012年4月24日Tuesday理论力学CAI31