建筑力学课件8

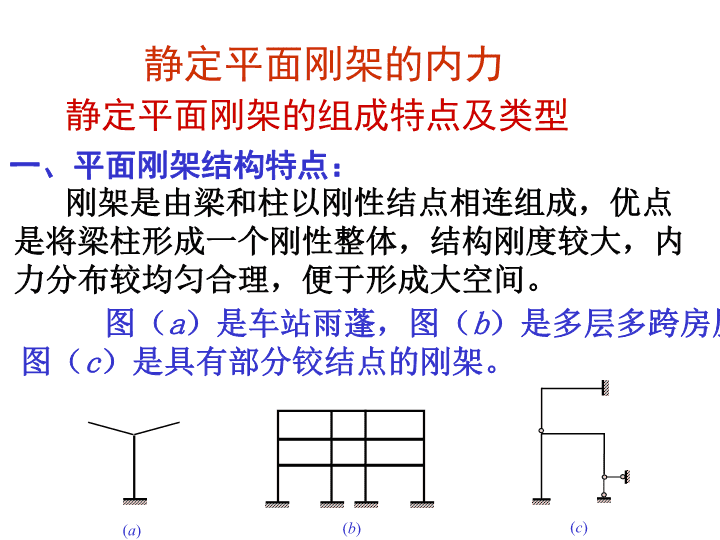
静定平面刚架的组成特点及类型刚架是由梁和柱以刚性结点相连组成，优点是将梁柱形成一个刚性整体，结构刚度较大，内力分布较均匀合理，便于形成大空间。(a)(b)(c)图（a）是车站雨蓬，图（b）是多层多跨房屋，图（c）是具有部分铰结点的刚架。一、平面刚架结构特点：静定平面刚架的内力 刚架是由梁柱组成的含有刚结点的杆件结构l刚架梁桁架弯矩分布均匀可利用空间大 2.静定刚架型式静定刚架的分类:简支刚架悬臂刚架单体刚架(联合结构)三铰刚架(三铰结构)复合刚架(主从结构) 刚架的梁与柱联结处在构造上为刚性联结，即当刚架受力而变形时，汇交于联结处的各杆端之间的夹角始终保持不变。这种结点称为刚结点。具有刚结点是刚架的持点。刚架的内力是指各杆件中垂直于杆轴的横截面上的弯矩、剪力和轴力。在计算静定刚架时，通常应由整体或某些部分的平衡条件，求出各支座反力和各铰接处的约束力，然后逐杆绘制内力图。3.刚架的特点：具有刚结点。刚架的内力： 静定结构的内力分析前述有关梁的内力图的绘制方法，对于刚架中的每一杆件同样适用。刚架杆件中一般有轴力，这是它们与梁的主要区别。应该指出，当荷载与杆轴垂直时，此杆的轴力沿杆轴无变化。 4.计算刚架内力的一般步骤:（1）首先计算支反力,一般支反力只有三个,由平衡方程求得。三铰刚架支反力有四个，须建立补充方程。（2）按“分段、定点、连线”的方法，逐个杆绘制内力图。说明：（a）M图画在杆件受拉的一侧。（c）汇交于一点的各杆端截面的内力用两个下标表示，例如：MAB表示AB杆A端的弯矩。↶MAB（b）、的正负号规定同梁。、图可画在杆的任意一侧，但必须注明正负号。 例作图示刚架的内力图一、求支座反力二、绘制内力图1、弯矩图2、剪力图3、轴力图 一、求支座反力由得由得由得由校核二、绘制内力图1、弯矩图：各控制截面弯矩图d图b右侧受拉右侧受拉 2、剪力图：由控制截面的弯矩值，即可绘出弯矩图。图C下边受拉校核：计算无误分别由图b、c、d所示隔离体，即可求得即可绘出剪力图3、轴力图：分别由图b、c、d所示隔离体，即可求得绘出轴力图 静定结构的内力分析返回为了校核所作剪力图和轴力图的正确性，可用任一截面截取出刚架的某一部分，检验其平衡条件是否得到满足。如右图绘制内力图如下： 例作图示刚架的内力图解：（1）计算支反力HA=48kN←，RB=42kN↑RA=22kN↓（2）逐杆绘M图CD杆：MDC=0MCD=48kN·m（左）CB杆：MBE=0MEB=MEC=126kN·m（下）MCB=192kN·m（下）AC杆:MAC=0MCA=144kN·m（右）（3）绘Q图CD杆：QDC=0,QCD=24kNCB杆：QBE=-42kN,QEC=-22kNAC杆：QAC=48kN,QCA=24kNRB=↑MCD=MEB=MEC=42×3=126kN·m（下）MCB=42×6-20×3=192kN·m（下）48由∑X=0可得：HA=6×8=48kN←由∑MA=0可得：由∑Y=0可得：（左）192126144RA↓←HARB↑ （4）绘N图（略）（5）校核:内力图作出后应进行校核。M图:通常检查刚结点处是否满足力矩的平衡条件。例如取结点C为隔离体（图a），∑MC=48－192+144=0满足这一平衡条件。Q(N)图：可取刚架任何一部分为隔离体，检查∑X=0和∑Y=0是否满足。例如取结点C为隔离体（图b），∑X=24－24=0∑Y=22－22=0满足投影平衡条件。（a）C48kN·m192kN·m144kN·m（b）C有:24kN022kN024kN22kN有： 刚架指定截面内力计算与梁的指定截面内力计算方法相同.例:求图示刚架1,2截面的弯矩解:连接两个杆端的刚结点,若结点上无外力偶作用,则两个杆端的弯矩值相等,方向相反. 练习:作图示结构弯矩图 练习:作图示结构弯矩图 拱的内力分析一般指杆的轴线为曲线形状，并且在竖向荷载作用下会产生水平支座反力的结构。 重要特点：竖向荷载产生水平推力（与梁相比）优点：M减小，FN为主——便于使用抗压材料：砖、石、混凝土缺点：水平反力要求——地基、支承结构、（墙、柱、墩等）更坚固。——可称拱式结构或推力结构 拱的种类：拱各部分的名称：两铰拱无铰拱三铰拱带拉杆的三铰拱带吊杆的三铰拱拉杆吊杆花篮螺丝 拱与曲梁的区别拱结构CAHBBHAVAVBP曲梁结构PBAHA=0VAVA三铰拱的内力计算一、拱的内力计算原理仍然是截面法。二、拱通常受压力，所以计算拱时，规定轴力以受压为正。三、实际计算时常将拱与相应简支梁对比，通过公式完成计算。这些公式为绘制拱的影响线提供了方便。 三铰拱的计算1、支座反力的计算由拱的整体平衡取左半拱为隔离体相应简支梁可得三铰拱的反力只与荷载及三个铰的位置有关，与拱轴线形状无关；推力FH与拱高f成反比。 三铰拱的计算2、内力的计算计算图a所示三铰拱K截面的内力取隔离体如图b相应简支梁相应简支梁K截面的弯矩为M0相应简支梁K截面的剪力为FS0相应简支梁K截面的轴力为FN0三铰拱的内力与荷载及三个铰的位置有关，与拱轴线形状有关；压力为正 例图(a)所示三铰拱的拱轴为半圆形。计算截面K1的内力。 建立截面上轴力、剪力方向上的投影方程及截面形心为矩心的力矩方程 三铰拱的计算例试作图a所示三铰拱的内力图。拱轴线为抛物线，方程为解：求支座反力，结果如图a。求内力，将拱沿水平方向分为8等分，如图a。 三铰拱的合理拱轴线合理拱轴线：拱上所有截面的弯矩都等于0（剪力也为0），只有轴力时的拱轴线。由得合理拱轴线方程例4-2试求图a所示对称三铰拱在图示荷载作用下的合理拱轴线。解：相应简支梁（图b）的弯矩方程为三铰拱的推力为合理拱轴线方程为 试求图示有水平拉杆的三铰拱在竖向荷载作用下的支座反力和内力。解：（1）计算支座反力（2）计算拉杆轴力PPP1P2P2P3P3AABBCCDDEEFFHVAVB1Il/2l/2l/2l/2ll拉杆flCFP3VBl/2BCF11NABHCVC（3）计算各截面内力作1-1截面，研究其右半部依截面法或拱的计算公式，可求得任意截面的内力。 带拉杆三铰拱可由拱上部整体的平衡条件求得全部支座反力。欲求拉杆AB中的拉力，只须用截面将铰C与拉杆截断，取任一侧为隔离体，以较C为矩心建立力矩方程即可。带拉杆三铰拱内力 桁架桥梁房屋建筑通讯国防机械 桁架的工程定义由一些细长直杆按适当方式分别在两端连接而成的几何形状不变的结构桁架概述 静定桁架一、概述桁架结构在机械工程中应用很广泛。特别是在钢结构中，桁架更是一种重要的结构型式。科学试验和理论分析的结果表明，各种桁架有着共同的特性：由于在结点荷载作用下，桁架中各杆的内力主要是轴力，而弯矩和剪力则很小，可以忽略不计，因而从力学的观点来看，各结点所起的作用和理想铰是接近的。 桁架简化计算的假设各杆件都用光滑铰链相连接 各杆件轴线都是直线，并通过铰链中心桁架简化计算的假设所有外力，包括荷载及支座约束力都作用在节点上 2.桁架计算简图的基本假定（1）各结点都是无摩擦的理想铰；(理想铰)（2）各杆轴都是直线，并在同一平面内且通过铰的中心；(平直杆)（3）荷载只作用在结点上并在桁架平面内。（力结点）实际结构与计算简图的差别（主应力、次应力） 二力杆轴向力ABFAFBAB概述桁架简化计算的假设理想桁架的内力特点： 3.桁架的各部分名称跨度L节间长度d桁高H下弦杆上弦杆腹杆斜杆竖杆 4.桁架的组成a.简单桁架：由一个铰结三角形依次增加二元体而组成的桁架；如b.联合桁架：由简单桁架按基本组成规则而联合组成的桁架；如 ABCDE联合桁架 1.求桁架内力的基本方法：结点法和截面法。2.结点法：3.在计算中，经常需要把斜杆的内力S分解为水平分力X和竖向分力Y。则由比例关系可知：XY一、计算桁架内力的方法所取隔离体只包含一个结点，称为结点法。LLxLy⌒SS⌒ 4.结点法计算举例（1）首先由桁架的整体平衡条件求出支反力。VA=45kNHA=120kNHB=120kN（2）截取各结点解算杆件内力。分析桁架的几何组成：此桁架为简单桁架，由基本三角形ABC按二元体规则依次装入新结点构成。由最后装入的结点G开始计算。（或由A结点开始）取结点G隔离体G15kNSGFSGEYGEXGE由∑Y=0可得YGE=15kN（拉）由比例关系求得XGE==20kN(拉)及SGE=15×=25kN(拉)再由∑X=0可得SGF=-XGE=-20kN(压）25-20-20+151520304050+60+600756045-120-45然后依次取结点F、E、D、C计算。ABCDEFG15kN15kN15kN4m4m4m3mF20kNSFE=+15kN15kNSFC=-20kNE+15kN+20kN+15kNYEC=-30kNXEC=-40kNSED=+60kN到结点B时，只有一个未知力SBA，最后到结点A时，轴力均已求出，故以此二结点的平衡条件进行校核。 30°30°30°30°aFPFPFPIGDBAHECaaa例试用节点法求出桁架中所有杆件的内力。FIyFAFIxxy解：30°30°30°30°aFPFPFPIGDBAHECaaaFIyFA平面汇交力系：CFPFNCAFNCBFNCDFNCExy 30°30°30°30°aFPFPFPIGDBAHECaaaFIyFA30°FAA约定各杆内力为拉力FNABFNACxy（压力）（拉力） 30°30°30°30°aFPFPFPIGDBAHECaaaFIyFAxy（拉力）FNBDBFNBC(+2.6FP)FNBA 30°30°30°30°aFPFPFPIGDBAHECaaaFIyFA（压力）（压力）xy30°30°30°CFPFNCAFNCBFNCDFNCE(-3FP)(0) 30°30°30°30°aFPFPFPIGDBAHECaaaFIyFA+2.6FP+2.6FP+2.6FP+2.6FP00-FP-FP+FP-3FP-3FP-2FP-2FP 桁架中内力为零的杆件称为零杆。出现零杆的情况可归结如下：(1)两杆结点上无荷载作用时，则该两杆的内力都等于零。(2)三杆结点上无荷载作用时，如果其中有两杆在一直线上，则另一杆必为零杆。上述结论都不难由结点平衡条件得到证实。在分析桁架时，可先利用上述原则找出零杆，这样可使计算工作简化。 1).两根杆的结点a).若结点上无荷载，则二杆全为零。a)b).若荷载沿其中一杆的方向，则该杆轴力为F，另一杆为零杆。b) 2).有单杆的结点a).在图示荷载作用下单杆3的轴力利用Fy=0可求。b).在荷载沿单杆作用下，则单杆轴力等于F，另两杆轴力相等。c).单杆结点上无荷载作用，则单杆轴力等于0。b)Fa)αc)F 练习:试指出零杆 零杆的判断，如：几点结论：（1）结点法适用于简单桁架，从最后装上的结点开始计算。（2）每次所取结点的未知力不能多于两个。（3）计算前先判断零杆。0000000000000 试用结点法解算图a所示桁架中各杆的内力解：1、首先求出支座反力2、用结点法计算各杆内力3、将此桁架各杆的内力注在图上 1、首先求出支座反力以整个桁架为隔离体，由得由得 静定结构的内力分析2、用结点法计算各杆内力取结点1为隔离体(图b)由得再由得再依次取结点2、3、4、5、6、7、8为隔离体计算 静定结构的内力分析最后可根据结点8的隔离体是否满足平衡条件来作校核。3、将此桁架各杆的内力注在图上 截面法：截面法是作一截面将桁架分成两部分，任取一部分为隔离体（含两个以上的结点），用平衡方程计算所截杆件的内力（一般内力不超过三个）。 截面单杆：任意隔离体中，除某一杆件外，其它所有待求内力的杆件均相交于一点时，则此杆件称为该截面的截面单杆。截面单杆的内力可直接根据隔离体平衡条件求出。截面法：截面法是作一截面将桁架分成两部分，任取一部分为隔离体（含两个以上的结点），用平衡方程计算所截杆件的内力（一般内力不超过三个）。 Oy 例：设支反力已求出。RARB求EF、ED、CD三杆的内力。作截面Ⅰ-Ⅰ，ⅠⅠ取左部分为隔离体。SEFSEDSCD由∑ME=0有RAd－P1d－P2×0－SCDh=0得（拉）（拉）XEF由∑MD=0有RA×2d－P1×2d－P2d+XEFH=0得（压）可以证明：简支桁架在竖向荷载作用下，下弦杆受拉力，上弦杆受压力。add∽XEDYED由∑MO=0有－RAa+P1a+P2(a+d)+YED(a+2d)=0YEFRA∽ SEFSEDSCDXEFaddXEDYEDYEFRA静定结构的内力分析 求DG杆内力作Ⅱ—Ⅱ截面，ⅡⅡ取左部分为隔离体。XDGYDG由∑Y=0有RA－P1－P2－P3+YDG=0YDG=SDGsin=－(RA－P1－P2－P3)上式括号内之值恰等于相应简支梁上DG段的剪力，故此法又称为剪力法。RA 几点结论：(1)用截面法求内力时，一般截断的杆件一次不能多于三个(特殊情况例外)。(2)对于简单桁架，求全部杆件内力时，应用结点法；若只求个别杆件内力，用截面法。(3)对于联合桁架，先用截面法将联合杆件的内力求出，然后再对各简单桁架进行分析(见图)。 ABCDEⅠⅠ a4×ahFP123AKBCDEOGHIJFAyFK123KOGHIJFKFN1FN2FN3mm 静定结构是无多余约束的几何不变体系；其全部内力和反力仅由平衡条件就可唯一确定。超静定结构是有多余约束的几何不变体系；其全部内力和反力仅由平衡条件不能完全确定，而需要同时考虑变形条件后才能得到唯一的解答。1、在几何组成方面，静定结构是没有多余约束的几何不变体系。在静力学方面，静定结构的全部反力和内力均可由静力平衡条件求得，且其解答是唯一的确定值。静定结构的内力分析和受力特点 3、温度改变、支座移动和制造误差等因素在静定结构中不引起内力－t°Ct°C2、材料及其截面形状和尺寸由于只用静力平衡条件即可确定静定结构的反力和内力，因此其反力和内力只与荷载以及结构的几何形状和尺寸有关，而与构件所用材料及其截面形状和尺寸无关。 4、静定结构的局部平衡特性在荷载作用下，如果静定结构中的某一局部可以与荷载平衡，则其余部分的内力必为零。P2PPaaaaPP局部平衡部分也可以是几何可变的只要在特定荷载作用下可以维持平衡PP影响的范围只限于该力系作用的最小几何不变部分 ＝+当静定结构的一个几何不变部分上的荷载作等效变换时，其余部分的内力不变。5、静定结构的荷载等效特性2PBAPPBAP2PPBA仅AB杆受力，其余杆内力为零除AB杆内力不同，其余部分的内力相同。结论：桁架在非结点荷载作用下的内力，等于桁架在等效荷载作用下的内力，再叠加上在局部平衡荷载作用下所产生的局部内力。 对静定结构来说，所能建立的独立的平衡方程的数目=方程中所含的未知力的数目。为了避免解联立方程应按一定的顺序截取单元，尽量使一个方程中只含一个未知量。qa↓↓↓↓↓↓↓↓↓↓↓qaABCDEFABC↓↓↓↓↓↓↓↓↓↓↓CDDEFYAXAYCXCXCYCXDYDYDXDYBYFYE二、静定结构的受力分析 1、单元的形式及未知力结点：杆件：杆件体系：桁架的结点法、刚架计算中已知FQ求FN时取结点为单元。多跨静定梁的计算、刚架计算中已知M求FQ时取杆件为单元。桁架的截面法取杆件体系为单元。未知力的数目是由所截断的约束的性质决定的。截断链杆只有未知轴力；在平面结构中，截断梁式杆，未知力有轴力、剪力和弯矩；在铰处截断，有水平和竖向未知力。 2、单元平衡方程的数目不一定等于单元上的未知力的数目3、计算的简化a)选择恰当的平衡方程，尽量使一个方程中只含一个未知量;b)根据结构的内力分布规律来简化计算;①在桁架计算中先找出零杆,常可使简化计算;②对称结构在对称荷载作用下,内力和反力也是对称的;;c)分析几何组成,合理地选择截取单元的次序;①主从结构,先算附属部分,后算基本部分;②简单桁架,按去除二元体的次序截取结点;③联合桁架,先用截面法求出连接杆的轴力,再计算其它杆。 一、几种典型结构：梁、刚架、拱、桁架、组合结构。二、{无推力结构：梁、梁式桁架有推力结构：三铰拱、三铰刚架、拱式桁架、组合结构三、杆件{链杆弯杆组成桁架组成梁、刚架组合结构为达到物尽其用，尽量减小杆件中的弯矩。①在静定多跨梁中，利用杆端负弯矩可减小跨中正弯矩；②在推力结构中，利用水平推力可减小弯矩峰值；③在桁架中，利用杆件的铰结及荷载的结点传递，使各杆处于无弯矩状态；三铰拱采用合理拱轴线可处于无弯矩状态。链杆只有轴力，无弯矩，截面上正应力均布，充分利用了材料的强度。弯杆有弯矩，截面上正应力不均布，没有充分利用材料强度。三、各种结构形式的受力特点 返回↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ql2/80.207l0.207l0.207lql2/48ql2/48fql2/32ff/6ql2/48ql2/48无弯矩状态↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓7f/125f/12l/4l/4l/4l/4ql2/192ql2/192无弯矩状态简支梁M最大(使用于小跨度结构)；伸臂梁、多跨静定梁、三铰刚架、组合结构M次之(使用于较大跨度结构)；桁架、具有合理轴线的三铰拱M为零(使用于大跨度结构)。