建筑力学课件9

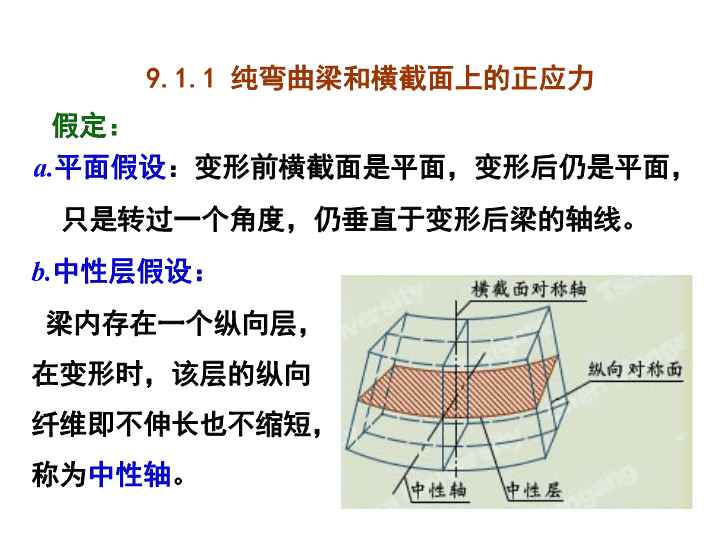
平面弯曲纯弯曲横力弯曲内力只有弯矩内力有弯矩和剪力B20kNA1m1mD20kN1mCABDC20202020Q图(kN)ABDC2020M图(kN·m)CD段CA、DB段9.1梁内正应力、强度条件 假定：a.平面假设：变形前横截面是平面，变形后仍是平面，只是转过一个角度，仍垂直于变形后梁的轴线。b.中性层假设：梁内存在一个纵向层，在变形时，该层的纵向纤维即不伸长也不缩短，称为中性轴。9.1.1纯弯曲梁和横截面上的正应力 zydAM力矩平衡M：横截面上的弯矩y：所求正应力点处到中性轴的距离Iz：截面对中性轴的惯性矩z纯弯曲理论也适用于横力弯曲,(横力会发生翘曲、纤维之间会挤压） 等截面梁内的最大应力发生在弯矩最大的截面，且是距中性层最远的地方。有拉应力和压应力宽b、高h的矩形直径为D的圆截面轧制型钢（工字钢、槽钢等）的WZ从型钢表中查得尽可能使截面面积分布在里中性轴较远的地方 1．强度校核9.1.2正应力强度条件2．截面设计3.计算容许荷载 例1：图示矩形梁，材料的[σ]=170MPa，试对该梁作强度校核。2kNA2mB1m5kNC2020z20单位：mm 解：2kNA2mB1m5kNC(1)绘内力图AB和BC段，斜直线ABCM图(kN·m)MB=0kN·m24弯矩图:MC=2×1=2kN·mMA=2×3－5×2=-4kN·m0 (2)确定截面的几何参量2020z20(3)强度校核不安全 (3)讨论b×h=20mm×40mm时b×h=20mm×100mm时 提高弯曲强度的一些措施弯曲正应力强度条件：在[]一定时，提高弯曲强度的主要途径：（一）选择合理截面（1）矩形截面中性轴附近的材料未充分利用，工字形截面更合理。1.根据应力分布的规律选择z （2）为降低重量，可在中性轴附近开孔。 2.根据材料特性选择塑性材料：宜采用中性轴为对称轴的截面。脆性材料：宜采用中性轴为非对称轴的截面，例如T字形截面：ycz拉边压边即使最大拉、压应力同时达到许用应力值。 （二）合理安排载荷和支承的位置，以降低值。1.荷载尽量靠近支座：LABF0.5LLABF0.8LLABF0.9LLABF 2.将集中力分解为分力或均布力。LABF0.5L0.25LABF0.5L0.25L 3、合理安排支座位置及增加支座——减小跨度，减小。ABF0.6L0.2L0.2LABFL （三）选用合理结构1.等强度梁设计思想：按M(x)的变化来设计截面，采用变截面梁——横截面沿着梁轴线变化的梁。 2.桁架整体桁架——受弯构件桁架中单个杆件——受轴向拉压 3.拱ABF——提高强度——压应力使截面上拉应力降低，可使抗拉能力差的材料充分利用。 弯矩产生正应力剪力产生剪应力横力弯曲梁的横截面上9.2.1剪应力9.2梁内剪应力、强度条件研究对象（一般不验算）(1)矩形梁截面(2)工字形梁截面(3)圆形梁截面(1)弯矩较小、剪力很大时（深梁）(2)焊接组合梁腹板较小时(3)木梁（中性层剪切破坏） (1)矩形梁截面的剪应力(1)截面上各点剪应力方向与Q方向一致假定：(2)剪应力沿截面宽度方向均匀分布。 zyaaybA*h/2h/2剪应力计算式Q：横截面上剪力b：计算点处横截面宽度Iz:整个横截面对中性轴的惯性矩S*z：面积矩 zyaaybA*h/2h/2剪应力计算式 (1)沿高度方向抛物线分布(2)梁上下表面处剪应力为零结论:(3)y=0时，剪应力值最大 (2)工字型截面梁的剪应力主要考虑工字型截面梁腹板上的剪应力计算。剪应力计算式d:腹板宽度A* (1)沿腹板高度方向抛物线分布(2)腹板上下边处剪应力最小结论:(3)y=0时，剪应力值最大 (3)圆形截面梁的剪应力实心圆截面：最大剪应力在中性轴上空心圆环：z 合理截面（1）矩形木梁的合理高宽比R北宋李诫于1100年著«营造法式»一书中:矩形木梁的合理高宽比(h/b=1.5)英(T.Young)于1807年著«自然哲学与机械技术讲义»一书中:矩形木梁的合理高宽比bh梁的合理截面和变截面梁 （2）在面积相等的情况下，选择抗弯模量大的截面zDzaaa12a1z0.8a2a21.6a22a2z 应力状态的概念1.一点的应力状态:过一点不同方向面上应力的集合。σ1σ2σ3主平面:剪应力为零的平面主应力:主平面上的正应力主方向:主平面的法线方向梁的主应力、主应力迹线 三种应力状态（单向、二向、三向）σ1σ2σ3单向应力状态：三个主应力中只有一个不为零单向应力状态也称为简单应力状态二向和三向应力状态统称为复杂应力状态二向应力状态（平面应力状态）：两个主应力不为零三向应力状态（空间应力状态）：三个主应力皆不为零 9.4.2梁的主应力迹线AB实线主拉应力迹线虚线主压应力迹线 ABAB弯起钢筋受拉钢筋 9.5.1材料的两种破坏形式无数实验证明，材料的破坏主要有两种形式：脆性破坏:材料破坏时无明显的塑性变形，断口粗糙。9.5二向应力状态下的强度条件一强度理论常见的脆性材料铸铁、石料、陶瓷、高分子材料 2.塑性破坏:材料破坏时有显著的塑性变形（即屈服现象）钢、铜、铝、聚合材料常见的塑性材料 强度理论的概念长期以来，人们根据对材料破坏现象的分析，提出过各种各样的假说，认为材料的某一类型的破坏是由某种因素引起的，这种假说就称为强度理论。1.适用于脆性破坏的强度理论第一强度理论（最大拉应力理论）第二强度理论（最大拉应变理论）2.适用于塑性屈服的强度理论第三强度理论（最大剪应力理论）第四强度理论（形状改变比能理论） 9.6弯曲中心弯曲中心:集中力作用在此点，扭矩为零yzPAτyτxτxτy:产生弯曲效应τx:产生扭转效应在A点作用集中力P作用在A点:无扭矩，A点称为弯曲中心 yzCA两个矩形中线的交点yzCAyzCA与形心重合常用几种薄壁截面的弯曲中心