隧道工程课程设计计算书1

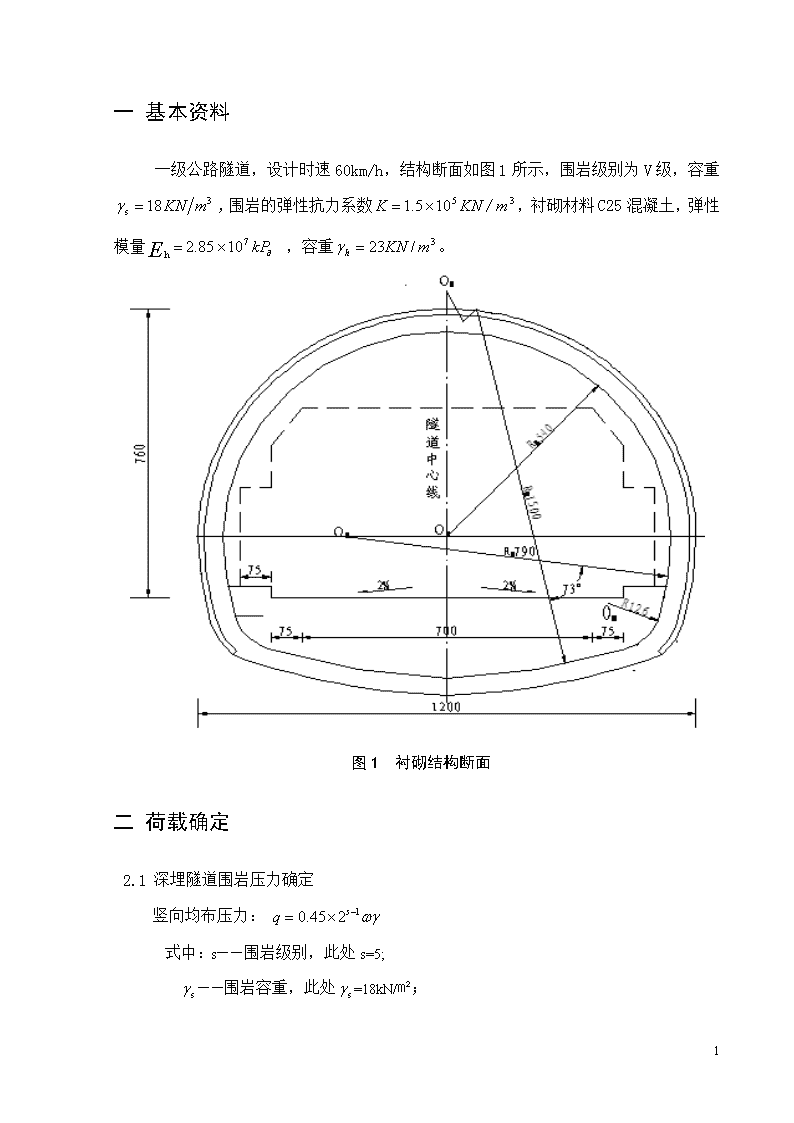
目录一基本资料1二荷载确定1三衬砌几何要素23.1衬砌几何尺寸23.2半拱轴线长度S及分段轴长△S23.3割分块接缝重心几何要素3四计算位移44.1单位位移44.2载位移——主动荷载在基本结构中引起的位移54.3载位移——单位弹性抗力及相应的摩擦力引起的位移84.4墙低（弹性地基上的刚性梁）位移12五解力法方程13六计算主动荷载和被动荷载（）分别产生的衬砌内力13七最大抗力值的求解15八计算衬砌总内力16九衬砌截面强度检算（检算几个控制截面）169.1拱顶（截面0）169.2截面（7）179.3墙低（截面8）偏心检查17十内力图17 一基本资料一级公路隧道，设计时速60km/h，结构断面如图1所示，围岩级别为V级，容重，围岩的弹性抗力系数/，衬砌材料C25混凝土，弹性模量，容重。图1衬砌结构断面二荷载确定2.1深埋隧道围岩压力确定竖向均布压力：式中：s——围岩级别，此处s=5;——围岩容重，此处=18kN/㎡；6 ——跨度影响系数，=1+i(Bm-5)，毛洞跨度Bm=12.00m，Bm=5~15时，i=0.1，此处:=1+0.1×（12.00-5）=1.7所以：kPa考虑到初期之处承担大部分围岩压力，而二次衬砌一般作为安全储备，故对围压力进行折减，对于本隧道按照40%折减，即q=(1－40%)×220.32=132.19kPa围岩水平均布力：e=0.4×q=0.4×132.19=52.88kPa2.2浅埋隧道围岩压力确定荷载等效高度=，分界深度2.5×7.35=18.38m（1）埋深（H）小于或等于等效荷载高度（）时竖向均布压力：在隧道埋深7m处kPa围岩水平均布力：（2）埋深（H）大于、小于或等于时竖向均布压力：式中：——作用在支护结构上的均布荷载；——围岩的天然容重；6 ——隧道埋深；——侧压力系数；——破裂面摩擦角，此处取0.5因此：围岩水平均布力：三衬砌几何要素3.1衬砌几何尺寸内轮廓半径r1=5.4m，r2=7.9m；内径r1、r2所画圆曲线的终点截面与竖直轴的夹角=90°，=105°；二次衬砌厚度d=0.45m。此处墙底截面为自内轮廓半径r2的圆心向内轮廓墙底做连线并延长至与外轮廓相交，其交点到内轮廓墙底间的连线。6 外轮廓线半径：R1=5.4+0.45=5.85mR2=7.9+0.45=8.35m拱轴线半径：=5.4+0.5×0.45=5.625=7.9+0.5×0.45=8.125拱轴线各段圆弧中心角：=90°=15°3.2半拱轴线长度S及分段轴长△S分段轴线长度:半拱轴线长度为：S=S1+S2=8.8357+2.1271=10.9628m将半拱轴线等分为8段，每段轴长为：3.3割分块接缝重心几何要素（1）与竖直轴夹角,,另一方面，角度闭合差=0。6 各接缝中心点坐标可由图1中直接量出。四计算位移图2衬砌结构计算图4.1单位位移用辛普生法近似计算，按计算列表进行。单位位移的计算见表1单位位移计算如下：6 计算精度校核为：闭合差单位位移计算表表1截面Φ（°）sinΦcosΦx（m）y(m)d(m)1/Iy/Iy*y/I(1+y)2/I00.000.001.000.000.000.450.01131.690.000.00131.58113.960.240.971.360.170.450.01131.6921.863.63178.92227.710.470.892.620.650.450.01131.6984.9354.83356.27341.880.670.743.751.440.450.01131.69189.04271.59781.25455.840.830.564.652.470.450.01131.69324.49800.221580.77569.790.940.355.283.680.450.01131.69484.491783.932884.48683.750.990.115.595.010.450.01131.69659.593306.474757.23795.341.00-0.095.576.380.450.01131.69839.425355.177165.598105.000.97-0.265.327.780.450.01131.691023.787965.7010144.831185.183627.5919541.5327980.93注：1.I—截面惯性矩，2.不考虑轴力的影响6 4.2载位移——主动荷载在基本结构中引起的位移（1）每一楔块上的作用力竖向力：侧向力：自重力：式中：bi——衬砌外缘相邻两截面之间的水平投影长度，由图2量得：——衬砌外缘相邻两截面之间的竖直投影长度，由图2量得——接缝i的衬砌截面厚度。7 自重力：式中：di——接缝i的衬砌截面厚度，本设计为等厚度衬砌；作用在各楔体上的力均列入表2，各集中力均通过相应的图形的行心。（2）外荷载在基本结构中产生的内力。楔体上各集中力对下一接缝的力臂由图2中量得，分别记为内力按照下式计算（见图3）。弯矩：轴力：式中：图3内力计算图示载位移计算表表3截面sinΦcosΦΣ（Q+G)ΣEsinΦΣ（Q+G)cosΦΣE00.00001.00000.00000.00000.00000.00000.000010.24120.9705251.367712.963560.629912.580748.049220.46500.8853484.127149.7153225.119144.0125181.106630.66750.7446695.4745110.3856464.229282.1920382.037240.82740.5616865.7670189.3051716.3356106.3100610.025750.93850.3454988.3457282.5261927.562497.5845829.977960.99410.10881046.6216384.54791040.446541.8465998.600070.9957-0.09301061.0555489.32191056.4930-45.50691101.999980.9659-0.25881075.2391596.73301038.5734-154.43451193.007918 载位移的计算表表2截面集中力力臂QGE00.00000.00000.00000.00000.00000.00000.00000.00001237.184114.183612.96350.65130.67340.1244154.47809.55122218.575814.183636.75180.55020.61530.2775120.26048.72723197.163814.183660.67030.44190.49470.395687.12677.01664156.108914.183678.91950.28150.39450.514743.94475.59545108.395114.183693.22100.11360.26550.608012.31373.7657644.092314.1836102.02180.00000.11360.66540.00001.611370.250314.1836104.77400.0000-0.05040.68330.0000-0.714980.000014.1836107.41110.0000-0.16010.70060.0000-2.2708△x△y0.00000.00000.00000.00000.00000.00000.00000.00001.61270.00000.00001.35690.16610.00000.0000-165.641910.1986251.367712.96351.25940.4794316.57256.2147-627.615324.0012484.127149.71531.13850.7912551.178739.3347-1336.273240.6199695.4745110.38560.89951.0294625.5793113.6309-2165.643456.6784865.7670189.30510.62451.2160540.6715230.1950-3009.267767.8853988.3457282.52610.31281.3308309.1545375.9857-3763.904571.59211046.6216384.5479-0.01741.3667-18.2112525.5616-4342.132275.25221061.0555489.3219-0.25661.4011-272.2668685.5889-4828.435618 18 基本结构中，主动荷载产生弯矩的校核为：另一方面，从表2中得到闭合差（3）主动荷载位移（计算过程见表4）。主动荷载位移计算表表4截面(1+y)0　131.68720.00001.00000.00000.00000.00001-165.6419131.687221.85531.1661-21794.9868-3620.1473-25415.13422-627.6153131.687284.93421.6455-82580.9582-53306.0085-135886.96663-1336.2732131.6872189.03952.4367-175825.4226-252608.3846-428433.80724-2165.6434131.6872324.48683.4661-284953.0807-702722.7922-987675.87295-3009.2677131.6872484.48684.6821-395956.2768-1457950.6067-1853906.88346-3763.9045131.6872659.59216.0129-495250.5967-2482641.7162-2977892.31297-4342.1322131.6872839.42117.3796-571333.1783-3644877.1440-4216210.32238-4828.4356131.68721023.77638.7807-635320.4802-4943238.0606-5578558.5409　Σ-2663014.9802-13540964.8601-16203979.8403计算精度校核：闭合差：18 4.3载位移——单位弹性抗力及相应的摩擦力引起的位移（1）各接缝处的抗力强度抗力上零点假定在接缝3，最大抗力值假定在接缝6，最大抗力值以上各截面抗力强度按下式计算：查表1，算得最大抗力值以下各截面抗力强度按下式计算：式中：由图2中量得：则：按比例将所求得抗力绘于图2上。（2）各楔体上抗力集中力按下式计算：式中：—表示楔体i外缘长度，可以通过量取夹角，用弧长公式求得，的方向垂直于衬砌外缘，并通过楔体上抗力图形的形心。（3）抗力集中力与摩擦力的合力按下式计算：式中：—围岩于衬砌间的摩擦系数，此处取。则：其作用方向与抗力集中力的夹角18 ；由于摩擦力的方向与衬砌位移方向相反，其方向向上。将的方向线延长，使之交于竖直轴，量取夹角，将分解为水平和竖直两个分力：以上计算结果列入表5中。弹性抗力及摩擦力计算表表5截面30.00000.00001.44560.00000.00000.00001.00000.00000.000040.44070.22041.44560.318563.12270.89200.45210.28410.144050.80190.62131.44560.898274.90860.96550.26040.86720.233861.00000.90101.44561.302488.38640.99960.02821.30190.036770.75620.87811.41601.2434101.30990.9806-0.19611.2192-0.243880.00000.37811.41600.5354113.25480.9188-0.39480.4919-0.2114（4）计算单位抗力及其相应的摩擦力在基本结构中产生的内力弯矩：轴力：式中：—力至接缝中心点的力臂，由图2量得。计算见表6及表7.计算表表6截面40.47040.1498　　　　　　　　-0.149851.83320.58390.71150.6352　　　　　　-1.219163.16031.00662.07051.84850.78411.0212　　　　-3.876374.45631.41933.39883.03442.14382.79210.85881.0678　　-8.313785.77041.83794.76054.25023.54384.61542.27912.83381.10590.5921-14.129418 计算表表7截面　455.83510.82740.56160.14400.11920.28410.1596-0.0365569.79390.93850.34540.37780.35461.15130.3977-0.0479683.75270.99410.10880.41450.41212.45320.26700.1078795.33890.9957-0.09300.17070.16993.6724-0.34170.51528105.00000.9659-0.2588-0.0407-0.03934.1643-1.07781.019318 18 （5）单位抗力及相应摩擦力产生的载位移。计算见表8.单位抗力及相应摩擦力产生的载位移计算表表8截面4-0.1498131.6872324.48683.4661-19.7297-48.6154-68.38515-1.2191131.6872484.48684.6821-160.5400-590.6386-751.66466-3.8763131.6872659.59216.0129-510.4604-2556.7833-3069.34727-8.3137131.6872839.42117.3796-1094.8075-6978.6925-8079.24158-14.1294131.68721023.77638.7807-1860.6642-14465.3694-16337.9346　Σ-3646.2019-24640.0992-28306.5729校核为：闭合差：4.4墙底（弹性地基上的刚性梁）位移单位弯矩作用下的转角：主动荷载作用下的转角：单位抗力及相应摩擦力作用下的转角：18 五解力法方程衬砌矢高计算力法方程的系数为：以上将单位抗力及相应摩擦力产生的位移乘以，即为被动荷载的载位移。求解方程为：式中：式中：，以上解的值应带入原方程，校核计算。六计算主动荷载和被动荷载（）分别产生的衬砌内力计算公式为：18 计算过程列入表9、10。.主、被动荷载作用下衬砌弯矩计算表表9截面00.0000402.68460.0000402.68460.0000-1.96430.0000-1.96431-165.6419402.684695.0114332.05410.0000-1.96430.3427-1.62162-627.6153402.6846369.2346144.30400.0000-1.96431.3319-0.63243-1336.2732402.6846821.8117-111.77700.0000-1.96432.96451.00024-2165.6434402.68461410.6422-352.3166-0.1498-1.96435.08862.97445-3009.2677402.68462106.2105-500.3726-1.2191-1.96437.59764.41426-3763.9045402.68462867.4460-493.7740-3.8763-1.964310.34364.50307-4342.1322402.68463649.2167-290.2309-8.3137-1.964313.16372.88578-4828.4356402.68464450.664724.9136-14.1294-1.964316.0547-0.0390主、被动荷载作用下衬砌轴力计算表表10截面　　　00.0000572.0134572.01340.00002.06342.0634148.0492555.1215603.17070.00002.00252.00252181.1066506.3990687.50560.00001.82671.82673382.0372425.9135807.95070.00001.53641.53644610.0257321.2293931.2550-0.03651.15881.12235829.9779197.57231027.5503-0.04790.71270.66486998.600062.24651060.84650.10780.22450.332371101.9999-53.22391048.77600.5152-0.19200.323281193.0079-148.04801044.95991.0193-0.53400.4853七最大抗力值的求解首先求出最大抗力方向内的位移。考虑到接缝5的径向位移与水平方向有一定的偏离，因此修正后有：18 计算过程列入表11，位移值为：最大抗力值为：最大抗力位移修正计算表表11截面　053028.4075-258.67325.0129265826.1037-1296.7027143727.2781-213.53994.8468211937.3714-1034.9853219002.9855-83.27574.367482993.6387-363.69843-14719.5949131.71183.5762-52640.2151471.02774-46395.5823391.69412.5468-118160.2689997.56665-65892.6618581.29941.3308-87689.9543773.59326-65023.7105592.98850.00000.00000.0000　Σ302266.6754-453.1988八计算衬砌总内力按下式计算衬砌总内力：计算过程列入表12.计算精度的校核为以下内容：根据拱顶切开点的相对转角和相对水平位移应为零的条件来检查：18 式中：闭合差：式中：闭合差：衬砌总内力计算表表12截面MpMσ[M]NpNσ[N]eM/IMy/I0402.68-1005.38-602.69572.011056.101628.11-0.37-79366.960.001332.05-829.96-497.91603.171024.911628.08-0.31-65567.77-10881.852144.30-323.67-179.36687.51934.961622.46-0.11-23619.61-15233.923-111.78511.92400.14807.95786.361594.310.2552693.7875642.924-352.321520.861168.54931.25574.401505.650.78153882.06379176.595-500.371698.761198.391027.55340.261367.810.88157812.34580603.146-493.77671.54177.771060.85170.101230.950.1423409.47117252.877-290.23-688.73-978.961048.78165.431214.20-0.81-128915.96-821756.19824.91-691.85-666.941044.96248.361293.32-0.52-87827.37-682796.63　Σ2499.99-377993.07九衬砌截面强度检算（检算几个控制截面）9.1拱顶（截面0）e=0.0370m<0.45d=0.2025m（可）又有：e=0.0370m<0.2d=0.09m可得18 式中：—混凝土极限抗压强度，取9.2截面（7）e=0.081m<0.2d=0.09m9.3墙低（截面8）偏心检查其他各截面偏心距均小于0.45d.十内力图将内力计算结果按比例绘制成弯矩图M与轴力图N，如图4所示。图4衬砌结构内力图18 18 18 9.2截面（7）e=0.081m<0.2d=0.09m9.3墙低（截面8）偏心检查其他各截面偏心距均小于0.45d.十内力图将内力计算结果按比例绘制成弯矩图M与轴力图N，如图4所示。图4衬砌结构内力图18