岩土力学课件--第8章土体中的应力计算

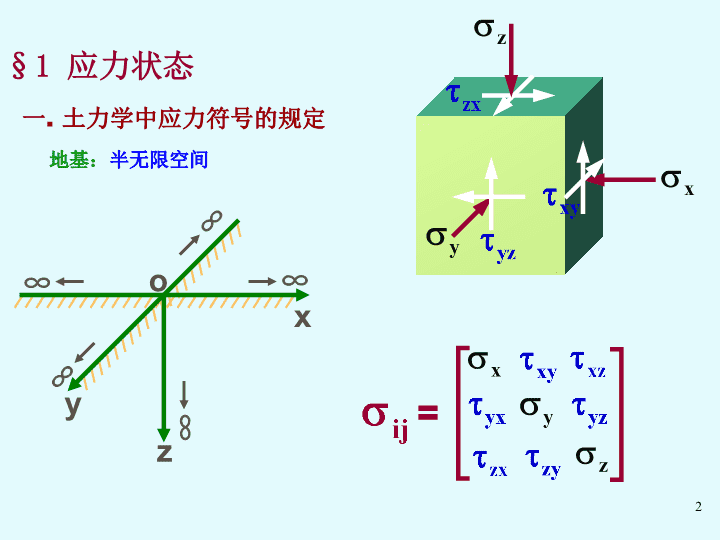
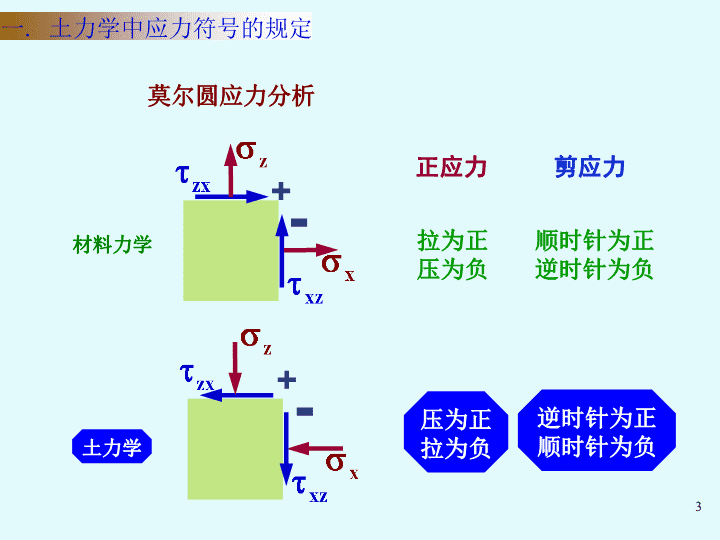
土体中的应力计算第八章1 yzx∞∞∞∞∞o一.土力学中应力符号的规定§1应力状态=地基：半无限空间2 一.土力学中应力符号的规定莫尔圆应力分析材料力学+-+-土力学正应力剪应力拉为正压为负顺时针为正逆时针为负压为正拉为负逆时针为正顺时针为负3 二.地基中常见的应力状态yzxo1.一般应力状态——三维问题==4 2.轴对称三维问题应变条件应力条件独立变量：二.地基中常见的应力状态==0000000000005 yzxo3.平面应变条件——二维问题沿长度方向有足够长度，L/B≧10；垂直于y轴切出的任意断面的几何形状均相同，其地基内的应力状态也相同；平面应变条件下，土体在x,z平面内可以变形，但在y方向没有变形。二.地基中常见的应力状态6 应变条件应力条件独立变量二.地基中常见的应力状态==0000000007 4.侧限应力状态——一维问题水平地基半无限空间体；半无限弹性地基内的自重应力只与Z有关；土质点或土单元不可能有侧向位移侧限应变条件；任何竖直面都是对称面应变条件AB二.地基中常见的应力状态yzxo8 ③均匀一致各向同性体（土层性质变化不大时）②线弹性体（应力较小时）①连续介质（宏观平均）与(x,y,z)无关与方向无关碎散体非线性弹塑性成层土各向异性Δσεεpεe线弹性体加载卸载三.土的应力-应变关系的假定9 §地基中自重应力的计算假定：水平地基半无限空间体半无限弹性体侧限应变条件一维问题定义：在修建建筑物以前，地基中由土体本身的有效重量而产生的应力。目的：确定土体的初始应力状态10 自重应力：由于土体本身自重引起的应力确定土体初始应力状态土体在自重作用下，在漫长的地质历史时期，已经压缩稳定，因此，土的自重应力不再引起土的变形。但对于新沉积土层或近期人工充填土应考虑自重应力引起的变形。11 一、竖向自重应力天然地面11zzσczσcz=z土体中任意深度处的竖向自重应力等于单位面积上土柱的有效重量12 二、成层土的自重应力计算说明：1.地下水位以上土层采用天然重度，地下水位以下土层采用浮重度2.非均质土中自重应力沿深度呈折线分布天然地面h1h2h3321水位面1h11h1+2h21h1+2h2+3h313 三、水平向自重应力天然地面z静止侧压力系数14 四、例题分析【例】一地基由多层土组成，地质剖面如下图所示，试计算并绘制自重应力σcz沿深度的分布图15 57.0kPa80.1kPa103.1kPa150.1kPa194.1kPa16 注意:1.对于地下水位经下的土层,土体采用有效重度来计算.2.当地层中的不透水层(例如岩层或只含结合水的坚硬粘性土层),由于不透水层中不存在水的浮力,层面以下的自重应力按上覆土层的水土总重来计算.17 地下水位升降及填土对自重应力的影响:地下水位下降地下水位上升填土原水位原水位变化后水位变化后水位填土面天然地面18 2.分布规律自重应力在等容重地基中随深度呈直线分布；自重应力在成层地基中呈折线分布；在土层分界面处和地下水位处发生转折。自重应力分布线的斜率是容重；均质地基成层地基19 例:某地基土层的物理性质指标为:第一层为粉土,厚度5米,,,第二层为粉质粘土,厚度3米,,,,第三层为岩石层.地下水位在地面下2米处.求:土的自重应力分布20 §基底压力计算基底压力：基础底面传递给地基表面的压力，也称基底接触压力。基底压力附加应力地基沉降变形基底反力基础结构的外荷载上部结构的自重及各种荷载都是通过基础传到地基中的。上部结构基础地基建筑物设计暂不考虑上部结构的影响，使问题得以简化；用荷载代替上部结构。21 一.影响因素基底压力基础条件刚度形状大小埋深大小方向分布土类密度土层结构等荷载条件地基条件22 抗弯刚度EI=∞→M≠0；分布:中间小,两端无穷大。二.基底压力分布基础抗弯刚度EI=0→M=0；基础变形能完全适应地基表面的变形;基础上下压力分布必须完全相同，若不同将会产生弯矩。条形基础，竖直均布荷载弹性地基,完全柔性基础弹性地基,绝对刚性基础23 弹塑性地基，有限刚度基础二.基底压力分布—荷载较小—荷载较大砂性土地基粘性土地基—接近弹性解—马鞍型—抛物线型—倒钟型24 根据圣维南原理，基底压力的具体分布形式对地基应力计算的影响仅局限于一定深度范围；超出此范围以后，地基中附加应力的分布将与基底压力的分布关系不大，而只取决于荷载的大小、方向和合力的位置。三.实用简化计算基底压力的分布形式十分复杂简化计算方法：假定基底压力按直线分布的材料力学方法基础尺寸较小荷载不是很大25 BLPBP’BP’BLPBP’荷载条件竖直中心竖直偏心倾斜偏心基础形状矩形条形P’—单位长度上的荷载三.实用简化计算BLPoxy基础形状与荷载条件的组合26 exeyLBxyxyLBPP矩形面积中心荷载矩形面积偏心荷载27 eL/6:出现拉应力区xyLBeexyLBexyLBa3aPPPa=L/2-e矩形面积单向偏心荷载28 LePPPvPh倾斜偏心荷载分解为竖直向和水平向荷载，水平荷载引起的基底水平应力视为均匀分布。条形基础竖直偏心荷载29 说明:F—上部结构传至基础顶面的竖向力(kN)G—基础自重及其上的土重.,其中d为基础埋深,一般自室外地面标高算起;当室内外高差较大时,取平均值.注意:有地下水时,要扣除地下水位以下的部分基础及回填土的浮力.30 例2:某柱下方形基础边长为2米,埋深为1.5米.柱传给基础的竖向力F=800kN,地下水位于地表下0.5米处.求:基底压力F=800kN2m1.5m0.5m31 例3:已知基础底面长3米,宽2米,基底弯矩M=147kN.m,竖向力N=490kN求:基底压力（偏心距沿长度方向）N=490kNM=147kN.m32 680kN1.31m4m例4：某建筑物基础，在设计地面标高处作用有偏心荷载680kN,偏心距1.31m,基础埋深2m,底面尺寸为长4m,宽2m.求:基底平均压力和边缘最大压力.33 7.5基底附加应力在建筑物建造之前,土中已存在着自重应力。由于建筑物等荷载作用在土中产生的附加原有应力之上的应力，称为附加应力。由于天然地层形成年代长久,在本身自重应力作用下的变形早已完成.因此,只有附加应力才能产生新的变形.34 7.5基底附加应力的计算有埋深的情况下,基底附加应力的计算公式为:--为基底标高以上天然土层的加权平均重度,其中地下水位以下的土层的重度取有效重度.D--为基础埋深,米,一般从室外地面算起,对于新填土场地则应从老天然地面算起.35 h=1mh=3mF例5:某框架独立柱基,承受轴心荷载F=400kN,地下水位深0.5米，基础埋深3米。第一层土重度18kN/m3,第二层土饱和重度20kN/m3.求:基底附加压力36 一.竖直集中力作用下的附加应力计算－布辛内斯克(Boussinesq)yzxoPMxyzrRβM’（P；x,y,z；R,α,β）α37 查表38 位移分量:39 附加应力分布规律距离地面越深，附加应力的分布范围越广在集中力作用线上的附加应力最大，向两侧逐渐减小同一竖向线上的附加应力随深度而变化在集中力作用线上，当z＝0时，σz→∞，随着深度增加，σz逐渐减小竖向集中力作用引起的附加应力向深部向四周无限传播，在传播过程中，应力强度不断降低（应力扩散）40 二.矩形面积竖直均布荷载作用下的附加应力计算1.角点下的垂直附加应力——Boussinesq解的应用矩形竖直向均布荷载角点下的应力分布系数查表4-5pMm=L/B,n=z/B41 a.矩形面积内b.矩形面积外两种情况：角点法叠加原理角点下垂直附加应力的计算公式地基中任意点的附加应力42 注意:1.要使角点M位于所划分的每一个矩形的公共角点.2.所划分的矩形面积总和应等于原有受荷面积.3.查表时,所有分块矩形都是长边为L,短边为B43 三.矩形面积三角形分布荷载作用下的附加应力计算矩形面积竖直三角分布荷载角点下的应力分布系数查表4-8ptM44 注意:1.B是沿三角形分布荷载方向的边长.2.坐标原点在三角形荷载的零点处45 例:如图,求m点下深度Z=2m处的附加应力m3m3m3m3m200kPa400kPa46 五.竖直线布荷载作用下的附加应力计算－弗拉曼解--B氏解的应用M47 六.条形面积竖直均布荷载作用下的附加应力计算任意点下的附加应力—F氏解的应用条形面积竖直均布荷载作用时的应力分布系数pM查表4-1048 七.条形面积其它分布荷载作用下的附加应力计算表4-10八.圆形面积均布荷载作用时圆心下的附加应力计算查表4-9r--圆形面积的半径49 九.影响土中应力分布的因素(1)上层软弱，下层坚硬的成层地基2.非均匀性—成层地基中轴线附近σz比均质时明显增大的现象—应力集中；应力集中程度与土层刚度和厚度有关；随H/B增大，应力集中现象逐渐减弱。(2)上层坚硬，下层软弱的成层地基中轴线附近σz比均质时明显减小的现象—应力扩散；应力扩散程度，与土层刚度和厚度有关；随H/B的增大，应力扩散现象逐渐减弱。1.非线性和弹塑性应力水平较高时影响较大(3)土的变形模量随深度增大的地基—应力集中现象H均匀成层E1E2>E1H均匀成层E1E2