岩土力学课件--地基沉降计算第8章

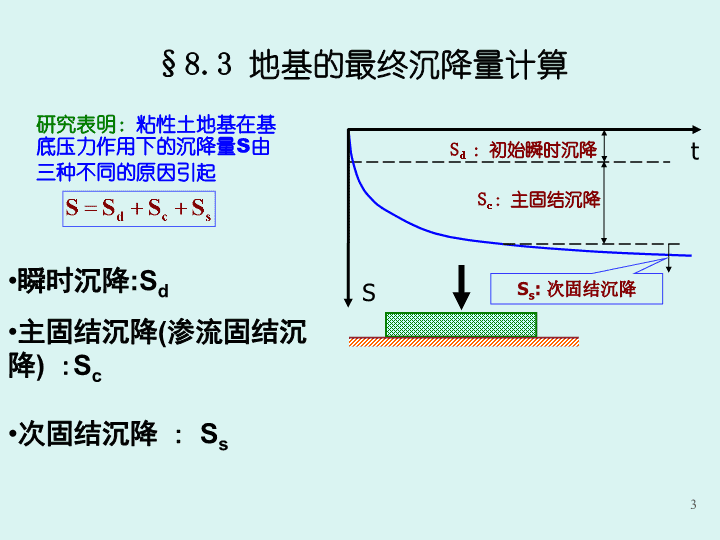
第8章地基变形1 在荷载作用下，土体的沉降通常可以分为三部分：（1）瞬时沉降：施加荷载后，土体在很短的时间内产生的沉降。（2）主固结沉降：它是由饱和粘性土在荷载作用下产生的超静孔隙水压力逐渐消散，孔隙水排出，孔隙体积减小而产生的。（3）次固结沉降：指孔隙水压力完全消散，主固结沉降完成后的那部分沉降。通常认为次固结沉降是由于颗粒之间的蠕变及重新排列而产生的。2 研究表明：粘性土地基在基底压力作用下的沉降量S由三种不同的原因引起次固结沉降:Ss瞬时沉降:Sd主固结沉降(渗流固结沉降):SctSSd：初始瞬时沉降Ss:次固结沉降Sc：主固结沉降§8.3地基的最终沉降量计算3 一、分层总和法地基最终沉降量地基变形稳定后基础底面的沉降量1.基本假设地基是均质、各向同性的半无限线性变形体，可按弹性理论计算土中应力在压力作用下，地基土不产生侧向变形，可采用侧限条件下的压缩性指标为了弥补假定所引起误差，取基底中心点下的附加应力进行计算，以基底中点的沉降代表基础的平均沉降2.单一压缩土层的沉降计算在一定均匀厚度土层上施加连续均布荷载，竖向应力增加，孔隙比相应减小，土层产生压缩变形，没有侧向变形。4 △p∞∞可压缩土层H1H0s土层竖向应力由p1增加到p2，引起孔隙比从e1减小到e2，竖向应力增量为△p由于所以3.单向压缩分层总和法分别计算基础中心点下地基中各个分层土的压缩变形量△si,基础的平均沉降量s等于△si的总和ei第i层土的压缩应变5 4.单向压缩分层总和法计算步骤e1i———由第i层的自重应力均值从土的压缩曲线上得到的相应孔隙比e2i———由第i层的自重应力均值与附加应力均值之和从土的压缩曲线上得到的相应孔隙比ei土的压缩应变1.绘制基础中心点下地基中自重应力和附加应力分布曲线2.确定地基沉降计算深度3.确定沉降计算深度范围内的分层界面4.计算各分层沉降量5.计算基础最终沉降量6 绘制基础中心点下地基中自重应力和附加应力分布曲线确定基础沉降计算深度一般取附加应力与自重应力的比值为20％处，即σz=0.2σc处的深度作为沉降计算深度的下限确定地基分层1.不同土层的分界面与地下水位面为天然层面2.每层厚度hi≤0.4b计算各分层沉降量根据自重应力、附加应力曲线、e-p压缩曲线计算任一分层沉降量对于软土，应该取σz=0.1σc处，若沉降深度范围内存在基岩时，计算至基岩表面为止计算基础最终沉降量d地基沉降计算深度σc线σz线7 6m下降后地下水位原地下水位2m中砂粉质粘土例:图示天然地基，由粉质粘土和中砂组成，。粉质粘土在水面以上的重度为，在地下水位以下的重度为,试求由于地下水位下降引起粉质粘土层中2m~6m土层的沉降量压力P(kPa)孔隙比e500.671000.651500.632000.6188 二、《规范》法由《建筑地基基础设计规范》（GB50007－2002）提出分层总和法的另一种形式沿用分层总和法的假设，并引入平均附加应力系数和地基沉降计算经验系数均质地基土，在侧限条件下，压缩模量Es不随深度而变，从基底至深度z的压缩量为附加应力面积深度z范围内的附加应力面积附加应力通式σz=p0代入引入平均附加应力系数因此附加应力面积表示为因此9 利用附加应力面积A的等代值计算地基任意深度范围内的沉降量，因此第i层沉降量为根据分层总和法基本原理可得成层地基最终沉降量的基本公式zi-1地基沉降计算深度znzi△zzi-1534612b12345612aip0ai-1p0p0p0第n层第i层ziAiAi-110 地基沉降计算深度zn应该满足的条件zi、zi-1——基础底面至第i层土、第i-1层土底面的距离(m)ai、ai-1——基础底面至第i层土、第i-1层土底面范围内平均附加应力系数当确定沉降计算深度下有软弱土层时，尚应向下继续计算，直至软弱土层中所取规定厚度的计算沉降量也满足上式，若计算深度范围内存在基岩，zn可取至基岩表面为止当无相邻荷载影响，基础宽度在1～30m范围内，基础中点的地基沉降计算深度可以按简化公式计算为了提高计算精度，地基沉降量乘以一个沉降计算经验系数ys，可以查有关系数表得到地基最终沉降量修正公式11 三、地基沉降计算中的有关问题1.分层总和法在计算中假定不符合实际情况假定地基无侧向变形计算结果偏小计算采用基础中心点下土的附加应力和沉降计算结果偏大两者在一定程度上相互抵消误差，但精确误差难以估计2.分层总和法中附加应力计算应考虑土体在自重作用下的固结程度，未完全固结的土应考虑由于固结引起的沉降量相邻荷载对沉降量有较大的影响，在附加应力计算中应考虑相邻荷载的作用3.当建筑物基础埋置较深时，应考虑开挖基坑时地基土的回弹，建筑物施工时又产生地基土再压缩的情况12 四、例题分析【例】某厂房柱下单独方形基础，已知基础底面积尺寸为4m×4m，埋深d＝1.0m，地基为粉质粘土，地下水位距天然地面3.4m。上部荷重传至基础顶面F＝1440kN,土的天然重度＝16.0kN/m³,饱和重度sat＝17.2kN/m³，有关计算资料如下图。试分别用分层总和法和规范法计算基础最终沉降（已知fk=94kPa）3.4md=1mb=4mF=1440kN501002003000.900.920.940.96eσ13 【解答】A.分层总和法计算1.计算分层厚度每层厚度hi＜0.4b=1.6m，地下水位以上分两层，各1.2m，地下水位以下按1.6m分层2.计算地基土的自重应力自重应力从天然地面起算，z的取值从基底面起算z(m)σc(kPa)01.22.44.05.67.21635.254.465.977.489.03.计算基底压力4.计算基底附加压力3.4md=1mF=1440kNb=4m自重应力曲线附加应力曲线14 5.计算基础中点下地基中附加应力用角点法计算，过基底中点将荷载面四等分，计算边长l=b=2m，σz=4Kcp0,Kc由表确定z(m)z/bKcσz(kPa)σc(kPa)σz/σczn(m)01.22.44.05.67.200.61.22.02.83.60.25000.22290.15160.08400.05020.032694.083.857.031.618.912.31635.254.465.977.489.00.240.147.26.确定沉降计算深度zn根据σz=0.2σc的确定原则，由计算结果，取zn=7.2m7.最终沉降计算根据e-σ曲线，计算各层的沉降量15 z(m)σz(kPa)01.22.44.05.67.294.083.857.031.618.912.31635.254.465.977.489.0σc(kPa)h(mm)12001600160016001600σc(kPa)25.644.860.271.783.2σz(kPa)88.970.444.325.315.6σz+σc(kPa)114.5115.2104.597.098.8e10.9700.9600.9540.9480.944e20.9370.9360.9400.9420.940e1i-e2i1+e1i0.06180.01220.00720.00310.0021si(mm)20.214.611.55.03.4按分层总和法求得基础最终沉降量为s=Σsi=54.7mmB.《规范》法计算1.σc、σz分布及p0计算值见分层总和法计算过程2.确定沉降计算深度zn=b(2.5－0.4lnb)=7.8m3.确定各层Esi4.根据计算尺寸，查表得到平均附加应力系数16 5.列表计算各层沉降量△siz(m)01.22.44.05.67.200.61.22.02.83.6152925771615381617429e20.9370.9360.9400.9420.94054.77.8l/bz/b3.9aaz(m)0.25000.24230.21490.17460.14330.12050.113600.29080.51580.69840.80250.867608861aizi-ai-1zi-1(m)0.29080.22500.18260.10410.06510.0185Esi(kPa)7448△s(mm)20.714.711.24.83.30.9s(mm)55.6根据计算表所示△z=0.6m,△sn=0.9mm＜0.025Σsi=55.6mm满足规范要求6.沉降修正系数js根据Es=6.0MPa，fk=p0，查表得到ys=1.17.基础最终沉降量s=yss=61.2mm17 3.土的应力历史对土的压缩性的影响土的应力历史：土体在历史上曾经受到过的应力状态先期固结压力pc：土在其生成历史中曾受过的最大有效固结压力讨论：对试样施加压力p时，压缩曲线形状ppc正常压缩曲线，斜率陡，土体压缩量大土层的先期固结压力对其固结程度和压缩性有明显的影响，用先期固结压力pc与现时的土压力p0的比值描述土层的应力历史，将粘性土进行分类1.正常固结土先期固结压力等于现时的土压力pc＝p02.超固结土先期固结压力大于现时的土压力pc>p03.超固结土先期固结压力小于现时的土压力pc0附加应力:σz=p超静孔压:u=0有效应力:σ’z=p33 重点：一维渗流固结沉降与时间之间的关系：饱和土层的渗流固结固结沉降的速度？固结沉降的程度？问题：§8饱和土体的渗流固结理论不可压缩层可压缩层p34 §8饱和土体的渗流固结理论一、一维渗流固结理论（Terzaghi渗流固结理论）二、固结度的计算四、固结系数的测定三、有关沉降－时间的工程问题35 实践背景：大面积均布荷载p不透水岩层饱和压缩层σz=pp侧限应力状态一、一维渗流固结理论（Terzaghi渗流固结理论）1、物理模型2、数学模型（1）基本假定（2）基本变量（3）建立方程3、问题求解固结系数时间因数（1）求解思路（2）初始、边界条件（3）微分方程的解36 1、物理模型ppp附加应力:σz=p超静孔压:u=σz=p有效应力:σ’z=0渗流固结过程－变形逐渐增加附加应力:σz=p超静孔压:u0附加应力:σz=p超静孔压:u=0有效应力:σ’z=p37 2、数学模型①土层均匀且完全饱和；②土颗粒与水不可压缩；③变形是单向压缩（水的渗出和土层压缩是单向的）；④荷载均布且一次施加；——假定z=const⑤渗流符合达西定律且渗透系数保持不变；⑥压缩系数a是常数。（1）基本假定（2）基本变量总应力已知有效应力原理超静孔隙水压力的时空分布38 （3）建立方程微小单元（1×1×dz）微小时段（dt）2、数学模型孔隙体积的变化＝流出的水量土的压缩特性有效应力原理达西定律表示超静孔隙水压力的时空分布的微分方程超静孔隙水压力孔隙比超静孔隙水压力孔隙比土骨架的体积变化＝不透水岩层饱和压缩层z39 （3）建立方程2、数学模型固体体积：孔隙体积：dt时段内：孔隙体积的变化＝流出的水量40 （3）建立方程2、数学模型dt时段内：孔隙体积的变化＝流出的水量土的压缩性：有效应力原理：达西定律:孔隙体积的变化＝土骨架的体积变化41 Cv反映了土的固结性质：孔压消散的快慢－固结速度；Cv与渗透系数k成正比，与压缩系数a成反比；（cm2/s；m2/year，粘性土一般在10-4cm2/s量级）固结系数（3）建立方程2、数学模型42 线性齐次抛物线型微分方程式，一般可用分离变量方法求解。给出定解条件，求解渗流固结方程，就可以解出uz,t。3、方程求解（1）求解思路43 不透水岩层饱和压缩层σz=pp0zH:u=pz=0:u=0z=H:uz0zH:u=0（2）边界、初始条件3、方程求解z44 (3)微分方程的解时间因数m＝1，3，5，7······3、方程求解0zH:u=pz=0:u=0z=H:uz0zH:u=0基本微分方程：初始边界条件：微分方程的解：反映孔隙水压力的消散程度－固结程度45 H单面排水时孔隙水压力分布双面排水时孔隙水压力分布zz排水面不透水层排水面排水面HH渗流渗流渗流Tv=0Tv=0.05Tv=0.2Tv=0.7Tv=∞Tv=0Tv=0.05Tv=0.2Tv=0.7Tv=∞u0=pu0=p(3)微分方程的解3、方程求解时间因数m＝1，3，5，7······46 二、固结度的计算一点M：地层：一层土的平均固结度Uz,t=0～1：表征总应力中有效应力所占比例1、基本概念M47 2、平均固结度Ut与沉降量St之间的关系t时刻：确定St的关键是确定Ut确定Ut的核心问题是确定uz.t在时间t的沉降与最终沉降量之比48 §饱和土体的渗流固结理论不透水边界透水边界渗流12349 2)常见计算条件实践背景：H小，p大自重应力附加应力自重应力附加应力压缩土层底面的附加应力还不接近零应力分布：12534基本情况：3.地基沉降过程计算不透水边界透水边界50 3.地基沉降过程计算不透水边界透水边界渗流12351 （2）双面排水时3.地基沉降过程计算透水边界应力分布：12534基本情况：透水边界H52 1、求某一时刻t的固结度与沉降量tTv=Cvt/H2St=UtS53 2、求达到某一沉降量(固结度)所需要的时间Ut=St/S从Ut查表（计算）确定Tv54 3、根据前一阶段测定的沉降－时间曲线，推算以后的沉降－时间关系对于各种初始应力分布，固结度均可写成：已知：t1－S1t2－S2公式计算，计算t3－S355 四、固结系数确定方法固结系数Cv——反映固结速度的指标,Cv越大，固结越快。直接计算或直接量测误差太大经验方法56 ①垂直固结度计算根据固结理论推出垂直平均固结度为：式中：——垂直固结时间因数（无因次）；——垂直固结系数，；t——固结时间，如荷载是逐渐施加，则从加荷历时一半算起。57 ②径向固结度的计算：n——砂井影响范围的直径与砂井直径之比；58 平均固结度的计算：可按《建筑地基处理技术规范》（JGJ79-2002）来计算：59 例:砂井直径30cm,正方形布置,间距200cm,,其他条件如例6-4,求地基平均固结度60 61