最新大地测量学课件 地球椭球与测量计算PPT课件

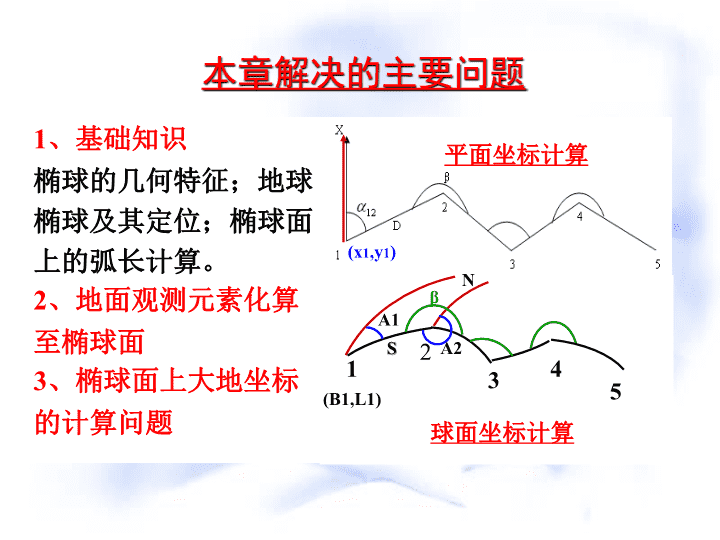
大地测量学课件地球椭球与测量计算 本章解决的主要问题1、基础知识椭球的几何特征；地球椭球及其定位；椭球面上的弧长计算。2、地面观测元素化算至椭球面3、椭球面上大地坐标的计算问题12345A1NA2S(B1,L1)平面坐标计算球面坐标计算β(x1,y1) §5.1.1椭球的几何参数及其关系应用大地测量学 应用大地测量学偏心距：第一偏心率：（5-1）第二偏心率：扁率：（5-2）椭球长半径a，短半径b§5.1.1椭球的几何参数及其关系 应用大地测量学a、b、e、e’之间的关系：（5-3）（5-4）（5-5）§5.1.1椭球的几何参数及其关系 应用大地测量学克拉索夫斯基椭球1980国家大地坐标系WGS-84a637824563781406378137b6356863.018776356755.288166356752.3142e20.006693421622970.006694384999590.00669437999013e′20.00673852544680.006739501819470.00673949674227f1:298.31:298.2571:298.257223563几种椭球几何参数§5.1.1椭球的几何参数及其关系 §5.1地球椭球及其定位应用大地测量学§5.1.1椭球的几何参数及其关系§5.1.2垂线偏差及其基本公式§5.1.3椭球定位 §5.1.2垂线偏差及其基本公式应用大地测量学垂线偏差——地面一点上，铅垂线方向和相应的椭球面法线方向之间的夹角u。垂线偏差u的分量——子午圈分量ξ和卯酉圈分量η计算公式：（5-7）（5-8） §5.1.2垂线偏差及其基本公式应用大地测量学天文方位角与大地方位角之间的关系式：（5-14）（5-15）以上公式称为拉普拉斯方程式。 §5.1.2垂线偏差及其基本公式应用大地测量学椭球短轴与地球某一固定历元的地轴不平行，起始大地子午面和起始天文子午面也不平行，将产生欧拉角，设为。此时垂线偏差公式（5-8）及拉普拉斯方程式（5-15）扩展为：（5-16）上式称为广义垂线偏差和拉普拉斯方程。 §5.1地球椭球及其定位应用大地测量学§5.1.1椭球的几何参数及其关系§5.1.2垂线偏差及其基本公式§5.1.3椭球定位 §5.1.3椭球定位应用大地测量学椭球定位——将一定参数的椭球与大地体的相关位置固定下来，确定测量计算基准面的具体位置和大地测量起算数据。包括：定位和定向两方面。定位是指确定椭球中心的位置，定向是指确定该椭球坐标轴的指向。从数学上讲就是要确定三个平移参数和三个旋转角度。椭球定位三个条件：（1）椭球短轴与某一指定历元的地球椭球自转轴平行；（2）起始大地子午面与起始天文子午面相平行；（3）在一定区域范围内，椭球面与大地水准面（或似大地水准面）最为密合。 §5.1.3椭球定位应用大地测量学椭球定位通过大地原点的天文观测实现。对于大地原点：B0=ψ0-ξ0L0=λ0-η0·secψ0A0=α0-η0·tanψ0H0=H0常+ζ0初期定位时，ξ0，η0，ζ0未知，可取为0。称为一点定位。根据大地测量和天文测量数据，在条件下，求出原点的ξ0，η0，ζ0值。称为多点定位。 第五章地球椭球及椭球面上的计算第一节地球椭球及其定位（基础）第二节椭球面上法截线曲率半径（基础）第三节椭球面上弧长计算（基础）第四节地面观测值归算至椭球面（重点）第五节椭球面上大地问题解算（重点） 第二节椭球面上法截线曲率半径应用大地测量学基本概念法截面——包含曲面一点法线的平面。法截线——法截面与曲面的截线。斜截线——不包含法线的平面与椭球面的截线。子午圈——包含短轴的平面与椭球面的交线。卯酉圈——与椭球面上一点子午圈相垂直的法截线，为该点的卯酉圈。平行圈——垂直于短轴的平面与椭球面的交线。 应用大地测量学§5.2.1卯酉圈曲率半径§5.2.2子午圈曲率半径§5.2.3任意方向的法截线曲率半径§5.2.4平均曲率半径§5.2.5曲率半径的数值计算公式§5.2椭球面上法截线曲率半径 应用大地测量学§5.2.1卯酉圈曲率半径§5.2.2子午圈曲率半径§5.2.3任意方向的法截线曲率半径§5.2.4平均曲率半径§5.2.5曲率半径的数值计算公式§5.2椭球面上法截线曲率半径 §5.2.1卯酉圈曲率半径应用大地测量学 应用大地测量学§5.2.1卯酉圈曲率半径微分几何中麦尼厄定理：（5-19）（5-26）（5-23）W又称第一基本纬度函数，V称为第二基本维度函数。 应用大地测量学§5.2.1卯酉圈曲率半径§5.2.2子午圈曲率半径§5.2.3任意方向的法截线曲率半径§5.2.4平均曲率半径§5.2.5曲率半径的数值计算公式§5.2椭球面上法截线曲率半径 §5.2.2子午圈曲率半径应用大地测量学（5-30） §5.2.2子午圈曲率半径应用大地测量学表M、N随B变化的规律BNM说明B=0°N0=aM0=a(1-e2)在赤道上，N为赤道半径a，M小于赤道半径a0°R>M 应用大地测量学§5.2.1卯酉圈曲率半径§5.2.2子午圈曲率半径§5.2.3任意方向的法截线曲率半径§5.2.4平均曲率半径§5.2.5曲率半径的数值计算公式§5.2椭球面上法截线曲率半径 §5.2.5曲率半径的数值计算公式应用大地测量学将N、M、R的计算公式（5-26）、（5-30）、（5-36）展开成微小参数的幂级数，取其前几项数值。克拉索夫斯基椭球参数代入得到（5-38）。1975年国际椭球参数代入得到（5-39）。 第五章地球椭球及椭球面上的计算第一节地球椭球及其定位（基础）第二节椭球面上法截线曲率半径（基础）第三节椭球面上弧长计算（基础）第四节地面观测值归算至椭球面（重点）第五节椭球面上大地问题解算（重点） 应用大地测量学（用于高斯投影计算，椭球面上大地问题解算）§5.3.1子午圈弧长计算§5.3.2平行圈弧长计算§5.3椭球面上弧长计算 应用大地测量学§5.3.1子午圈弧长计算§5.3.2平行圈弧长计算§5.3椭球面上弧长计算 应用大地测量学1、计算B=0到B的子午圈弧长X由M=dX/dB（5-27）得：将（5-37）代入上式，从0到B积分，可得X。可知，X是B的函数。见公式(5-41)。注意：将不同的椭球参数代入得相应的子午圈弧长计算式。§5.3.1子午圈弧长计算 应用大地测量学2、计算已知纬度B1和B2之间的子午圈弧长△X（1）分别计算0到B1和0到B2之间的子午圈弧长X1和X2，然后求△X=X2-X1；（2）用上述积分式求B1～B2之间的子午圈弧长△X。§5.3.1子午圈弧长计算 应用大地测量学§5.3.1子午圈弧长计算§5.3.2平行圈弧长计算§5.3椭球面上弧长计算 §5.3.2平行圈弧长计算应用大地测量学平行圈是一个半径等于r=N·COSB的圆，纬度B处经度L1～L2之间的平行圈弧长经度差相同，纬度不同的平行圈，弧长不同。纬度越高，单位经度差点平行圈弧长越短。用于计算中、小比例尺地形图中两条子午圈和两条平行圈所包围的椭球面面积。 第五章地球椭球及椭球面上的计算第一节地球椭球及其定位（基础）第二节椭球面上法截线曲率半径（基础）第三节椭球面上弧长计算（基础）第四节地面观测值归算至椭球面（重点）第五节椭球面上大地问题解算（重点） 应用大地测量学§5.4.1相对法截线§5.4.2大地线及其特征§5.4.3大地线微分方程和克莱劳方程§5.4.4地面观测方向归算至椭球面§5.4.5地面观测距离归算至椭球面§5.4.6椭球面上的三角形解算§5.4地面观测值归算至椭球面 应用大地测量学§5.4.1相对法截线§5.4.2大地线及其特征§5.4.3大地线微分方程和克莱劳方程§5.4.4地面观测方向归算至椭球面§5.4.5地面观测距离归算至椭球面§5.4.6椭球面上的三角形解算§5.4地面观测值归算至椭球面 §5.4.1相对法截线应用大地测量学CK=NsinB，（5-22）代入（5-21）得：所以：（5-43）上式说点的纬度不同，其法线与短轴的交点到椭球中心之间的距离不等，纬度越高，交点到椭球中心的距离越长。 §5.4.1相对法截线应用大地测量学设Q1和Q2两点既不在同一平行圈上，也不在同一子午圈上，它们的法线Q1n1和Q2n2不相交。法截线Q1m1Q2和Q2m2Q1称为两点间的相对法截线。正法截线与反法截线。一般不重合。 应用大地测量学正反法截线之间的夹角△近似公式：令Bm=45°，A=45°，不同距离S求得的△值为：S              △100km         0.042″60km          0.015″30km          0.004″在长距离的测量中，对向观测所得3个内角不能组成闭合三角形，需在两点间选择一条单一曲线——大地线。§5.4.1相对法截线 应用大地测量学§5.4.1相对法截线§5.4.2大地线及其特征§5.4.3大地线微分方程和克莱劳方程§5.4.4地面观测方向归算至椭球面§5.4.5地面观测距离归算至椭球面§5.4.6椭球面上的三角形解算§5.4地面观测值归算至椭球面 §5.4.2大地线及其特征应用大地测量学1、大地线——曲面上两点间的最短曲线。（或：大地线是曲面上的一条曲线，该曲线上每一点处的密切平面都包含曲面在该点的法线。 §5.4.2大地线及其特征应用大地测量学2、大地线几何特征（1）一般情况下，曲面上的曲线并不是大地线（如球面上的小圆）。大地线相当于椭球面上两点间的最短程曲线。（2）大地线与相对法截线间的夹角为δ=△/3。（3）大地线与相对法截线间的长度之差甚微，600km时二者之差仅为0.007mm。（4）两点位于同一条子午圈上或赤道上，则大地线与子午圈、赤道重合。 应用大地测量学§5.4.1相对法截线§5.4.2大地线及其特征§5.4.3大地线微分方程和克莱劳方程§5.4.4地面观测方向归算至椭球面§5.4.5地面观测距离归算至椭球面§5.4.6椭球面上的三角形解算§5.4地面观测值归算至椭球面 §5.4.3大地线微分方程和克莱劳方程应用大地测量学大地线的解析特性——表述dB、dL、dA与dS的关系：大地线的三个微分方程： 应用大地测量学大地线的解析特性——表述dB、dL、dA与dS的关系：大地线的克莱劳方程：r·sinA=C（C为常数）对于椭球面上一大地线而言，每点处平行圈半径与该点处大地线方位角正弦的乘积是一个常数（大地线常数）。——克劳莱定理§5.4.3大地线微分方程和克莱劳方程 应用大地测量学§5.4.1相对法截线§5.4.2大地线及其特征§5.4.3大地线微分方程和克莱劳方程§5.4.4地面观测方向归算至椭球面§5.4.5地面观测距离归算至椭球面§5.4.6椭球面上的三角形解算§5.4地面观测值归算至椭球面 §5.4.4地面观测方向归算至椭球面应用大地测量学将地面观测方向归算至椭球面上，包括三个基本内容：（1）将测站点铅垂线为基准的地面观测方向换算成椭球面上以法线为基准的观测方向。（垂线偏差改正）（2）将照准点沿法线投影至椭球面，换算成椭球面上两点间的法截线方向。（标高差改正）（3）将椭球面上的法截线方向换算成大地线方向。（截面差改正） §5.4.4地面观测方向归算至椭球面应用大地测量学1、垂线偏差改正δ1将地面测站点铅垂线为基准的观测方向换算成椭球面上以法线为准的观测方向，其改正数δ1为：（5-51）例：A=0°，tanα=0.01，ξ=η=5″，则δ1=0.05″。垂线偏差改正数的大小主要取决于测站点的垂线偏差和观测方向的天顶距（或垂直角）。仅在国家一、二等三角测量计算中，才规定加入此项改正。 应用大地测量学2、标高差改正δ2椭球上两点不在同一子午面或同一平行圈上，过两点多法线不共面，照准点B高出椭球面某一高度H2，使得在A点照准B点的法截线Ab′与Ab之间有一夹角δ2。（5-52）B2照准点的大地纬度；A1测站点至照准点的大地方位角；H2照准点高出椭球面的高程；M1测站点子午圈曲率半径。例：A1=45°，B2=45°，H2=2000m，δ1=0.1″局部地区的控制测量一般不必考虑此项改正。§5.4.4地面观测方向归算至椭球面 应用大地测量学3、截面差改正δ3将椭球面上法截线方向换算为大地线方向所加的为截面差改正数δ3。例：A1=45°，Bm=45°，S=30kmδ3=0.001″截面差改正主要与测站点至照准点间的距离有关。只有在国家一等三角测量计算中，才进行改正。§5.4.4地面观测方向归算至椭球面 应用大地测量学§5.4.1相对法截线§5.4.2大地线及其特征§5.4.3大地线微分方程和克莱劳方程§5.4.4地面观测方向归算至椭球面§5.4.5地面观测距离归算至椭球面§5.4.6椭球面上的三角形解算§5.4地面观测值归算至椭球面 §5.4.5地面观测距离归算至椭球面应用大地测量学设A、B两点的大地高分别为H1为H2，h=H2-H1，d为空间直线长。由三角形AOB按余弦公式可得：弦长（5-55）（4-28）（4-31）弧长 应用大地测量学§5.4.1相对法截线§5.4.2大地线及其特征§5.4.3大地线微分方程和克莱劳方程§5.4.4地面观测方向归算至椭球面§5.4.5地面观测距离归算至椭球面§5.4.6椭球面上的三角形解算§5.4地面观测值归算至椭球面 §5.4.6椭球面上的三角形解算应用大地测量学目的——将方向观测值和起算边长归算到椭球面上后，在椭球面上解算未知边长。方法一：按球面三角形解算公式：方法二：（勒让德定理）将球面三角形改化为对应边相等的平面三角形，按平面三角公式解算三角形求得球面边长。球面三角形球面角超ε=（A0+B0+C0）-180°=△/R2·ρ″，△为三角形面积。A1=A0-ε/3，B1=B0-ε/3，C1=C0-ε/3。 第五章地球椭球及椭球面上的计算第一节地球椭球及其定位（基础）第二节椭球面上法截线曲率半径（基础）第三节椭球面上弧长计算（基础）第四节地面观测值归算至椭球面（重点）第五节椭球面上大地问题解算（重点） 应用大地测量学§5.5.1概述§5.5.2勒让德级数式§5.5.3高斯平均引数正解公式§5.5.4高斯平均引数反解公式§5.5椭球面上大地问题解算 应用大地测量学§5.5.1概述§5.5.2勒让德级数式§5.5.3高斯平均引数正解公式§5.5.4高斯平均引数反解公式§5.5椭球面上大地问题解算 §5.5.1概述应用大地测量学（一）解算内容大地问题正解——已知P1点大地坐标（B1，L1）、P1P2大地线长S和大地方位角A1，推求P2点大地坐标（B2，L2）和大地方位角A2。大地问题反解——已知P1P2两点的大地坐标（B1，L1）、（B2，L2）反算P1P2的大地线长S和大地方位角A1、A2。 应用大地测量学（二）解算方法1、按解算的距离分为：短距离（<400km)、中距离（400～1000km)和长距离（1000～2000km)的解算。2、按解算形式分为：直接解法和间接解法直接解法——直接解求点B、A和相邻起算点的大地经差。间接解法——先求大地经差、纬差和大地方位角差，再加入到已知点的相应大地数据中。主要用于短距离大地问题的解算。§5.5.1概述 应用大地测量学（二）解算方法3、高斯平均引数大地问题解算公式（间接解法，适用于短距离）。基本思路：a、按照平均引数展开的泰勒级数把大地线两端点的经差、纬差和方位角差各表示为大地线长S的幂级数；b、利用大地线微分方程推求幂级数中各阶导数，最终得到大地问题解算公式。§5.5.1概述 应用大地测量学§5.5.1概述§5.5.2勒让德级数式§5.5.3高斯平均引数正解公式§5.5.4高斯平均引数反解公式§5.5椭球面上大地问题解算 应用大地测量学按照泰勒级数将P1和P2两点的纬差b、经差l和方位角差α展开成为大地线长度S的幂级数，成为勒让德级数式。公式（5-63）公式（5-69）公式（5-70）公式（5-71）§5.5.2勒让德级数式 应用大地测量学§5.5.1概述§5.5.2勒让德级数式§5.5.3高斯平均引数正解公式§5.5.4高斯平均引数反解公式§5.5椭球面上大地问题解算 §5.5.3高斯平均引数正解公式应用大地测量学（一）基本思想首先把勒让德级数在P1点展开改为在大地线长度中点M展开，以使级数公式项数减少、收敛快、精度高；其次，考虑到求定中点M的复杂性，将M点用大地线两端的平均纬度及平均方位角相对应的m点来代替，并借助迭代计算，便可顺利的实现大地问题的正解。 应用大地测量学（二）高斯平均引数正解公式推求步骤：1、经差l、纬差b、方位角差a是S的函数，故可以将其展为S的泰勒级数（按平均引数在S/2处展为S的幂级数）。2、引入大地线两端点的平均纬度和平均方位角，将dL/dS以Bm、Am按泰勒级数展开。3、根据大地线微分方程求泰勒级数中的系数。4、将系数代入平均引数公式。5、由于B2、A2未知，Bm、Am精确值未知，可通过逐次趋近法求出。一般三次即可。§5.5.3高斯平均引数正解公式 应用大地测量学（三）计算公式一般公式：公式（5-89）实用公式：距离小于70km时，采用简化公式：公式（5-90）§5.5.3高斯平均引数正解公式 应用大地测量学§5.5.1概述§5.5.2勒让德级数式§5.5.3高斯平均引数正解公式§5.5.4高斯平均引数反解公式§5.5椭球面上大地问题解算 §5.5.4高斯平均引数反解公式应用大地测量学高斯平均引数反解公式推求步骤：1、已知两点间的纬差b、经差l和平均纬度Bm，导出SsinAm和ScosAm，求a″。2、由SsinAm、ScosAm和a计算S和A1、A2。计算公式：公式（5-93）、（5-96） 第五章复习思考题1。名词定义：地球椭球、椭球定位、法截线、子午圈、卯酉圈、相对法截线、大地线、垂线偏差改正、标高差改正、截面差改正、大地问题正解、大地问题反解。2。写出N、M、R及子午圈弧长、平行圈弧长的计算公式，说明式中符号的意义。3。大地线微分方程的意义。4。地面观测值（方向、距离）归算至椭球面应加哪些改正？ 第五章习题1。已知图幅I-50-67中A、B点的大地纬度B=34°20′、34°，求相应的M、N、R。2。计算图幅I-50-67图廓长度。117°00′117°30′34°00′34°20′34°20′117°00′117°30′34°00′I-50-67ABCD 谢　谢！