控制测量学课件第6讲分解.ppt

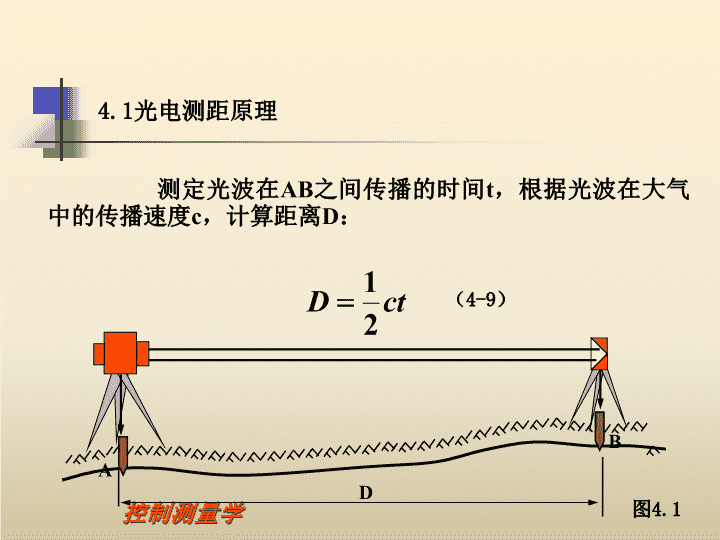
第6讲第4章电磁波测距仪及其距离测量 ABD4.1光电测距原理测定光波在AB之间传播的时间t，根据光波在大气中的传播速度c，计算距离D：图4.1（4-9） 4.2.1按测程分类1.短程光电测距仪：测程在3km以内;2.中程光电测距仪：测程在3～15km左右;3.远程激光测距仪：测程在15km以上。4.2.2按测距信号分类1.激光测距仪，主要用于长程测距仪；2.红外测距仪，用于中短程测距仪；4.2电磁波测距仪分类 4.2电磁波测距仪分类4.2.3按测距原理分类1.脉冲法测距：直接测定电磁波信号传播时间,较多地激光雷达、微波雷达等远距离测距上。2.相位法测距:通过测量光信号往返传播所产生的相位差间接的测定电磁波信号传播时间，多用于精密测距。 4.3脉冲法测距基本原理及应用测距仪中脉冲发生器发射一束光脉冲，其中一部分作为参考脉冲直接由仪器内部进入接收光电器件；其余光脉冲信号经过照准目标反射镜反射，作为回波脉冲也进入接收光电器件。测量参考脉冲同反射脉冲相继到达接受光电器件的时间相隔t，即可求出距离测量d。测量时间间隔的原理是:①.时标脉冲振荡器不断地产生间隔相同的脉冲信号；.测距瞬间参考脉冲打开电子门，使时标脉冲进入时标脉冲计数系统；.测距仪接收到回波脉冲信号，关闭电子门，时标脉冲计数系统停止计数；④.计数器统计的时标脉冲数乘以一个时标脉冲间隔电磁波传播距离，就是所测距离的二倍。 4.3脉冲法测距基本原理及应用计数显示电子门时标脉冲触发器脉冲发射脉冲接收反射器DBA图4.2 4.3脉冲法测距基本原理及应用脉冲式测距直接测量信号传播时间，由于电磁波信号以光速传播，设测量精度要求达到1cm，则时间间隔测量精度就要达到秒。这是很困难的，因而脉冲法测距主要用于长距离测距。由于GPS技术成为控制测量的首选技术手段，长距离测距仪应用价值不大，载波相位法因为测距精度高，成为测量仪器采用的主要测距方法。目前的脉冲式测距仪，一般用固体激光器发射出高频率的光脉冲，因而这类仪器可以不用反射棱镜，而是直接用被测目标对光脉冲产生的漫反射进行测距。在一些对测距精度要求不是太高的工程应用中（地形测量等），当测量地点难以到达时，这类仪器具有其它方法不可替代的独特优势。 4.4相位法测距基本原理及应用实质:利用测定光波在传播过程中的相位移φ,间接测定传播时间,实现距离的测量。图4.3 4.4相位法测距基本原理及应用相位式测距仪是通过测相电路测定调制光往返传播产生的相位差，乘以一个完整的相位对应的波长，求得待测距离。相位式测距仪的基本工作原理可用图4.3来说明。由光源发出的光经过调制器后，成为光强随高频信号变化的调制光射向反射棱镜，经反射棱镜反射回来被接收器接收。由于电磁波中一点的相位在传播过程中保持不变，所以通过相位计将反射信号的相位与光源处连续变化的相位比较，就可测定调制光由发射到接受这段时间内光源处的相位变化值。由图4.3可见，调制光全程的相位变化值为： 式(3-3)中，N为相位变化值中的整周期数，是不足一周的小数部分。设λ为调制光的波长，，则所测距离为式（3-4）称为相位法测距的基本公式，这种测距方法实际上相当于用一把长度为测尺λ／2来丈量所测距离。这一“尺子”称为测尺，令u=λ／2，则u称为尺长。4.4相位法测距基本原理及应用(4-18) 4.4相位法测距基本原理及应用在相位式测距仪中，相位计只能测定∆N，而不能测得N，因此距离d具有多值性而不能确定。为了测定距离，可以选择较长的测尺，即选择较低的调制频率。根据u=λ/2=c/2f，可以计算出测尺长度与相应的调制波频率的关系，如表4.1所示。由于测相误差一般为（周），所以测尺越长意味着测距精度越低，因此不能为了增加测程而简单地扩大尺长。实践中解决这个问题的方法是，用一组测尺组合来完成测距，以短测尺测定距离的尾数，以长测尺测定大数，就如同时钟中的时针、分针、秒针组合一样，既保证了精度，又解决了多值性的问题。 4.4相位法测距基本原理及应用 当所测距仪较长时,需要多个测尺共同测距。如精测尺和粗测尺频率相差较大，在技术上难以实现各个测尺频率具有相同的增益和稳定性。、实践中根据以两个频率f1、f2测量同一距离的相位差（φ1－φ2），就等于用其差频（f1－f2）测量距离时的相位差的原理，利用f1、f2测量结果，来间接求出其差频的测量结果。4.4相位法测距基本原理及应用 4.5干涉法测距基本原理干涉法测距本质上也是相位法测距，但是使用的测距信号不是经过调制的电磁波信号，并且测距需要反射镜沿测线方向移动。未经调制的光波波长很短，理论上测距精度很高，所以干涉法测距主要用于科学研究和工业测量，在控制测量领域未见应用报道。 4.6光波（电磁波）测距仪的合作目标测距仪的合作目标就是指反射棱镜。反射棱镜由光学玻璃制作，形状是四面锥体，其中三个互相垂直的面镀银作为反射面，另一平面是透射面。对于任意入射角的入射光线，只要与透射面垂直方向偏差在20度以内，经反射棱镜两个面上的反射，都能以入射方向反射出去。图4.4 4.7光波（电磁波）测距仪的检验仪器检验中最重要的两项参数检定是加常数和乘常数检定。加常数k是测距仪等效发射面偏离仪器对中线的距离，出厂时通过电路参数调整为0，但经过一段时间使用，可能会产生变化，所以需要经过检验。由于k是和距离无关的固定值，所以称为加常数。相位法测距测出相位差，乘以波长即得到距离,而波长等于光速除振荡频率。由于测距仪信号源电子元件参数会产生漂移，测距仪频率也会产生微小变化，因而需要进行检验。由于频率变化率r对距离的影响是和测距长度成比例的，所以称r为乘常数。测距仪测距精度很高，因而其检验工作复杂而精度要求更高，一般都是交专业机构在基线场完成。 4.8电磁波在大气中的传播本小节通篇内容杂乱、逻辑不清，给人感觉是根本没有经过整理的翻译初稿。许多描述不明其用意，根本用不着举例，文理不通处比比皆是！从中可以得到的结论是：看不懂不一定是自己因为水平低！大气对电磁波测距影响主要表现在两个方面：①.电磁波在大气中的传播速度小于真空中的传播速度；.由于大气折射，电磁波实际传播路径不是直线而是一弯曲波道轨迹。这两项影响都是使得测量距离较实际距离长。设地球曲率半径为r,波道曲率半径为R，K=R/r称为折光系数。对于光波测距（红外、激光），k=0.13,对于微波，k=0.25。 4.9测距成果的归算4.9.1概述归算改正包括倾斜改正、归算到参考椭球面的改正、投影到高斯平面的改正。注意：本小节第2句指出：“处于建立控制网等目的，长度值应化算为标石间的水平距离。”实际上测量标志中心间的水平距离，只是在仪器改正和气象改正基础上，作了倾斜改正，并不包含归算到参考椭球面和高斯投影面的改正，所以这句话是不对的。归算本质上是数据的换算，并不涉及到误差改正问题，因此速度改正理论上不属于归算问题。 4.9测距成果的归算4.9.2速度改正1.第1次速度改正测距仪显示距离计算公式为：公式中n参是生产厂家设置的参考折射率，c0是电磁波真空传播速度。实际长度应该为：第一次速度改正公式为：n是根据实际气象参数计算的平均折射率。推导（4－127）式时，由于n值接近1，（n参-n）是小量，所以取n为1。（4－123）（3－6）（4－127） 4.9测距成果的归算4.9.2速度改正2.第2次速度改正计算第1次速度改正时,采用测站和照准点处折射率平均值,而不是沿测线求折射率积分平均值。由此产生的差值，称为第2次速度改正。第1次速度改正实际上就是气象改正，仪器生产厂家根据参考气象条件，设置了改正公式内置于长度计算公式中。观测时可以根据实际气象条件输入，程序即按输入参数计算改正数。新型测距仪（全站仪）设计了气压、温度自动感应功能，可不需输入气象参数，自动根据测站气象条件计算第1次速度改正。第2次速度改正所谓沿测线折射率积分平均值,没有办法获得,因而这种改正更多是理论上的,未见实践中应用实例. 图4.5中p1、p2是两控制点，H1、H2是大地高。R、r是地球和测距弧线半径。α、β是椭球面弧长和测距波导弧线对应的圆心夹角。几何改正的任务就是：4.9.3几何改正图4.5 4.9.3几何改正第1次弧到弦：展开为级数取一次项，并顾及到k=R/r,就得到:图4.5(4-138) 4.9.3几何改正弦到弦的改正(d2→d3):在三角形p1p2C中，根据余弦定理,并顾及到就得到:(4-141)图4.5 4.9.3几何改正第2次弦到弧改正(d3→d4):将式:展开为级数,取一次项就得到:(4-152)图4.5 4.9.3几何改正一步公式:书上公式中多了一个S.关于精度分析,教材上得出公式为(4-158),从中得出的结论:在d1=1000m,∆H＝400m的条件下，若要使归算误差小于1mm，∆H误差要小于2.5mm,如高差不能以此精度测定的话,将使归算产生不能允许的误差。大地高高差精度达到2.5mm,是难以实现的。大地高和正常高有较大差别，但是大地高差很接近正常高差。大地测量距离较长,因而竖直角不大,并且归算误差也不需要精确到1mm，所以归算误差可以接受。工程控制网边长较短，但是控制范围较小，一般将地表视为平面，根本不做归算，所以不存在这个问题。(4-156) 4.9.3几何改正公式（4－158）中，后两项由于系数值较小，因而对Hm和R精度要求不高，第一项系数较大，因而对∆H精度要求较高。式（4－158）中第一项推导如下： 4.9.4投影改正大地坐标B、L、H（纬度、经度、大地高）属于曲面坐标，基准面是参考椭球面。由于曲面坐标计算复杂，应用非常不便，所以局部应用还是要转化为平面坐标。椭球面是不可展曲面，将椭球面上的值转换到平面，变形不可避免。高等级大地网由于控制面积很大，所以平差工作只能在椭球面完成。低等级的控制网覆盖范围较小，若在曲面上平差后，再将控制点大地坐标（B、L)转换为平面坐标，计算非常复杂。所以大地测量三四等网采取的做法是：将归算到椭球面的观测值，再转换为平面观测值，在平面上完成平差。由于将椭球面值转换到平面采用是高斯投影方法，所以投影平面称为高斯平面。本小节介绍将归算到椭球面上的距离观测值，投影到高斯平面的方法，由于相关内容在第8章（下册）中有详尽介绍，所以在此不讲述具体内容。 4.9.5电磁波测距成果化算示例本小节介绍了两个算例：1.长边化算:第1次速度改正值0.8938米，改正后距离为22396.560米,归算到椭球面的值为22389.312。归算改正总值－7.248米，其中d2→d3改正值为－7.254米。2.短边化算：第1次速度改正值0.0058米，仪器、棱镜常数改正数－0.00158米。改正后边长587.1240米，归算到椭球面后长度585.3687。归算改正总值-1.7553,其中d2→d3改正值为－1.756米。投影到高斯平面改正值和距中央子午线距离有关，放在第8章阐述。 4.9.5电磁波测距成果化算示例从两个实例可以得到的结论:1.当测站、照准点大地高值较大时，测边归算到参考椭球面，距离改正数较大。两个实例大地高均上了千米，5百多米的短边归算值都达到了1米多，长边更是达到了7米多。由此可知，在高海拔地区，大地点坐标反算的水平边长和实测值会有很大的差异。2.对于短边弧和弦之间的换算值（d1→d2、d3→d4）非常小，可以忽略不计,长边算例也仅仅-6.6mm。3.d2→d3改正可积分解为两步,第一步将d2改算为p1和p2沿法线下量（H2-H1)所得点的连线d6，称为倾斜改正，第二步将d6改算到d3,称为海水面改正。短边算例前两步改正不属于归算，第三步标题为海水面改正，实际上使用公式（4－165）是一步法公式d1→d4。顾及到（d1→d2、d3→d4）非常小，事实只上是包含倾斜和海水面改正两项，即改正d2→d3。 4.10光波测距的误差来源及精度估计相位式测距的基本公式为将其线性化并根据误差传播定律得测距误差：或者：（4－185）（4－187）（4－186） 4.10光波测距的误差来源及精度估计式（4－187）中的各项误差影响，就其方式来讲，有些是与距离成比例的，称为“比例误差”；另一些误差影响与距离长短无关。称为“固定误差”。测距仪精度即是以固定误差和比例误差表达的，其一般形式为：式中A是固定误差，单位是mm；B是比例误差，单位是ppm,D是测距长度，单位是米。（4－189） 4.11微波测距概要微波测距仪使用的测距信号是微波,其优点是测程远、对气象条件要求低、抗干扰性能强、不需精确照准，缺点是精度较低。微波测距仪不使用反射棱镜，而是采用两台接收机分别置于测线两端。测量工程中使用微波测距仪较少，微波测距仪较多地用于军事目的。4.12多波测距的理论基础阐述利用不同载波通过同样路径的差异，精确求解大气折射改正数的原理。