1. 您所在位置： > 建筑设计 > 建筑课件 > 结构力学课件：位移法2

结构力学课件：位移法2

  • 943.00 KB
  • 17页

结构力学课件：位移法2

  • 17页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档共5页，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，可选择认领，认领后既往收益都归您。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形，可联系本站下载客服投诉处理。
  4. 文档侵权举报电话：19940600175。
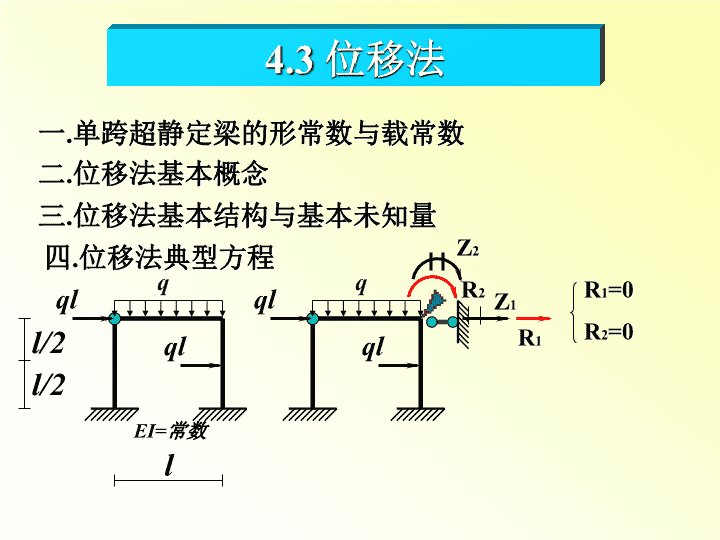
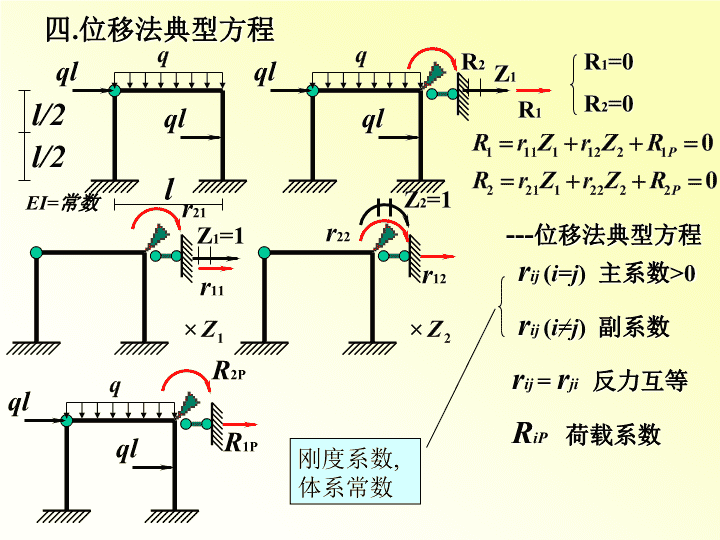
4.3位移法(DisplacementMethod) 一.单跨超静定梁的形常数与载常数4.3位移法二.位移法基本概念三.位移法基本结构与基本未知量四.位移法典型方程qll/2l/2EI=常数qllqlqlZ1Z2R2R1R1=0R2=0 四.位移法典型方程qll/2l/2EI=常数qllqlqlZ1Z2=1R2R1R1=0R2=0Z1=1r12r21r22r11qlqlR1PR2P---位移法典型方程rij(i=j)主系数>0rij=rji反力互等刚度系数,体系常数RiP荷载系数rij(i=j)副系数 qll/2l/2EI=常数qllqlqlZ1Z2=1R2R1R1=0R2=0Z1=1r12r21r22r11qlqlR1PR2PM2MPM1r11r12R1Pr21r22R2P 一.单跨超静定梁的形常数与载常数4.3位移法二.位移法基本概念三.位移法基本结构与基本未知量四.位移法典型方程五.算例例1.作M图ll/2lllEI1.5EIEIEIZ1Z2R2R1R1=0R2=0解: ll/2lllEI1.5EIEIEIZ1Z2R2R1Z1=1r11r21M1Z2=1r22r12M2R1PR2PMPr11r12R1Pr21r22R2P ll/2lllEI1.5EIEIEIZ1=1r11r21M1Z2=1r22r12M2R1PR2PMPM校核平衡条件 例2.作M图Z2R2R1=0R2=0解:lEIPllEIEI2EIR1Z1Pr21r11Z1=1Z2=1r22r12R2PR1PP3i/l12i/l12i/l3i/lM18i4i3iM2MPr11r12R1PPr21r22R2P0.24Pl0.13Pl0.39PlM 例3.作M图，EI=常数R1=0解:PllllZ1R1PM14iZ1=1r112i3iiMPR1PPPlr11R1PPM 例4.作M图，EI=常数R1=0解:R2=0PlllPllllPPZ2Z1 R1=0解:PlllPZ2Z1M1r11Z1=1r21M211=+R2PPR1PMPR2=0r22r12AR2PAPr12r22Z2=1 例5.作M图解:PlllEIlEIEIEIEIPZ2Z1Z1=1M1M2Z2=1r11r21r22PMP 作M图，EI=常数R1=0练习1:M14iZ1=1r112i3iir11llllZ1R1PMPR1PM 作M图，EI=常数R1=0练习2:Plllll/2l/2lP/2P/2P/2Z1=1M1MPP/2Z1 作M图R1=0练习3:lllEIEI2EIZ1M16i/lZ1=1MP 1)建立位移法基本体系,列出典型方程EI=常数练习4:llllZ4Z2Z3Z12)求出典型方程中系数r14,r32,R4P。 2)求出典型方程中系数r14,r32,R4P。Z4Z2Z3Z13i/lZ4=1r146i/l3i/l6i/lM4R4P=-ql/23ir324i3i6i/lM2Z2=12ir14=-3i/lR4PMPr32=2i

您可能关注的文档

相关文档

最近下载