结构力学课件11位移法.ppt

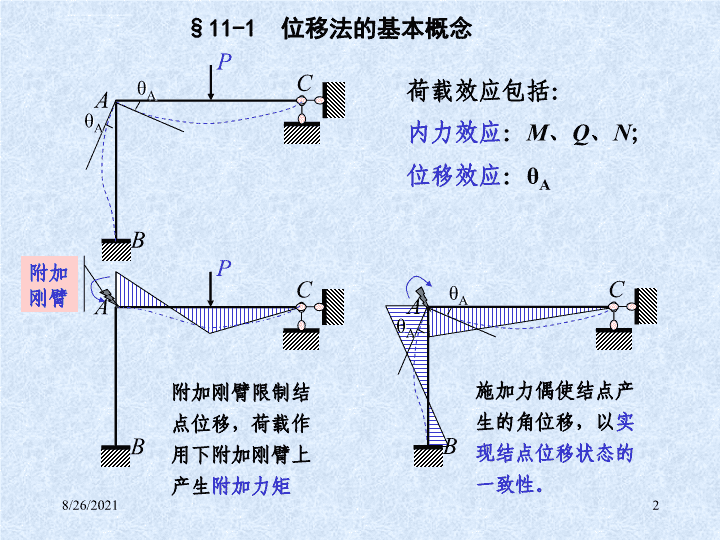
第十一章位移法8/26/20211 §11-1位移法的基本概念ABCPθAθA荷载效应包括：内力效应：M、Q、N；位移效应：θAABCPθAθA附加刚臂附加刚臂限制结点位移，荷载作用下附加刚臂上产生附加力矩施加力偶使结点产生的角位移，以实现结点位移状态的一致性。ABC8/26/20212 ABCPθAθA实现位移状态可分两步完成：分析：1）叠加两步作用效应，约束结构与原结构的荷载特征及位移特征完全一致，则其内力状态也完全相等；2）结点位移计算方法：对比两结构可发现，附加约束上的附加内力应等于0，按此可列出基本方程。1）在可动结点上附加约束，限制其位移，在荷载作用下，附加约束上产生附加约束力；2）在附加约束上施加外力，使结构发生与原结构一致的结点位移。8/26/20213 P12345BBAB选择基本未知量物理条件几何条件平衡条件变形条件8/26/20214 位移法基本作法小结:（1）基本未知量是结点位移；（2）基本方程的实质含义是静力平衡条件；（3）建立基本方程分两步——单元分析（拆分）求得单元刚度方程，整体分析（组合）建立位移法基本方程，解方程求出基本未知量;（4）由杆件的刚度方程求出杆件内力，画弯矩图。ABABCPCPA关于刚架的结点未知量8/26/20215 1MABMBA§11-2等截面杆件的刚度方程一、由杆端位移求杆端弯矩（1）由杆端弯矩MABMBAlMABMBA利用单位荷载法可求得设同理可得1杆端力和杆端位移的正负规定①杆端转角θA、θB，弦转角β＝Δ/l都以顺时针为正。②杆端弯矩对杆端以顺时针为正对结点或支座以逆时针为正。EI8/26/20216 EIMABMBAlMABMBA（2）由于相对线位移引起的A和B以上两过程的叠加我们的任务是要由杆端位移求杆端力，变换上面的式子可得：8/26/20217 ΔθAθB用力法求解单跨超静定梁X1X2Δ1/l1/lX2=112M1MX1=11令8/26/20218 可以将上式写成矩阵形式12348/26/20219 AMAB几种不同远端支座的刚度方程（1）远端为固定支座AMABMBA因B=0，代入(1)式可得（2）远端为固定铰支座因MBA=0，代入(1)式可得AMABMBA（3）远端为定向支座因代入（2）式可得lEIlEIlEI8/26/202110 由单位杆端位移引起的杆端力称为形常数。单跨超静定梁简图MABMBAQAB=QBA4i2iθ=1ABAB1AB10ABθ=13i0ABθ=1i－i08/26/202111 二、由荷载求固端反力mABEIqlEIqlmBA»在已知荷载及杆端位移的共同作用下的杆端力一般公式（转角位移方程）：8/26/202112 §11-3位移法的基本体系一、超静定结构计算的总原则:欲求超静定结构先取一个基本体系,然后让基本体系在受力方面和变形方面与原结构完全一样。力法的特点：基本未知量——多余未知力；基本体系——静定结构；基本方程——位移条件（变形协调条件）位移法的特点：基本未知量——基本体系——基本方程——独立结点位移平衡条件？一组单跨超静定梁8/26/202113 二、基本未知量的选取2、结构独立线位移：（1）忽略轴向力产生的轴向变形---变形后的曲杆与原直杆等长；（2）变形后的曲杆长度与其弦等长。上面两个假设导致杆件变形后两个端点距离保持不变。CDABCD12每个结点有两个线位移，为了减少未知量，引入与实际相符的两个假设：1、结点角位移数：结构上可动刚结点数即为位移法计算的结点角位移数。8/26/202114 线位移数也可以用几何方法确定。140将结构中所有刚结点和固定支座，代之以铰结点和铰支座，分析新体系的几何构造性质，若为几何可变体系，则通过增加支座链杆使其变为无多余联系的几何不变体系，所需增加的链杆数，即为原结构位移法计算时的线位移数。8/26/202115 8m4mii2iABCD3kN/mF1PABCDF2PABCD1F11F21ABCD2F12F2222F11+F12+F1P=0………………(1a)F21+F22+F2P=0………………(2a)三、选择基本体系四、建立基本方程8/26/202116 1.5i3(2i)2i4i2ABCDF12F22F11+F12+F1P=0………………(1a)F21+F22+F2P=0………………(2a)ABCD1F11F21ii2i=1k11k21=1k12k22=0………..(1)=0………..(2)k111+k122+F1Pk211+k222+F2Pk2104i6ik111.5ik12k22k11=10ik21=-1.5ik12=-1.5i8/26/202117 F1PABCDF2P4kN`·m4kN·mMPF2P040F1P-6F1P=4kN·mF2P=-6kN位移法方程：六、绘制弯矩图4.4213.625.691.4M(kN·m)ABCD五、计算结点位移8/26/202118 k111+k122+··········+k1nn+F1P=0k211+k222+··········+k2nn+F2P=0··································kn11+kn22+··········+knnn+FnP=0121=1k11k21k12k222=1k11×0+k21×1k21=k12=k12×1+k22×0kij=kji具有n个独立结点位移的超静定结构：8/26/202119