结构力学课件12.ppt

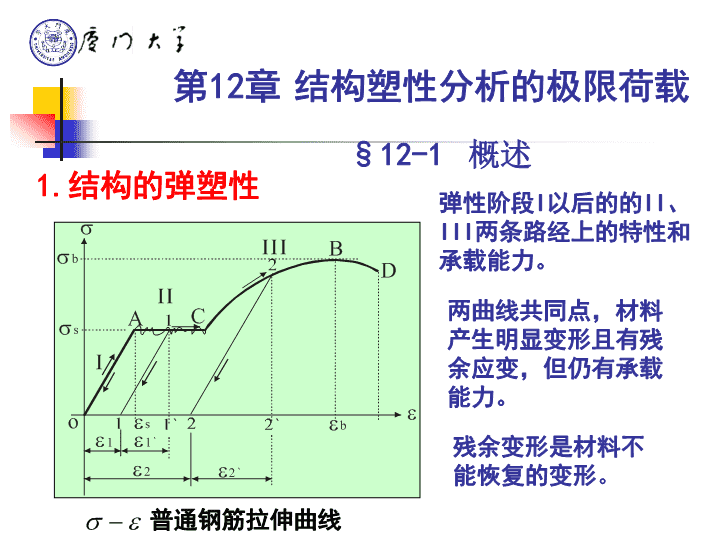
1.结构的弹塑性普通钢筋拉伸曲线第12章结构塑性分析的极限荷载§12-1概述弹性阶段I以后的的II、III两条路经上的特性和承载能力。两曲线共同点，材料产生明显变形且有残余应变，但仍有承载能力。残余变形是材料不能恢复的变形。 弹性设计方法:结构上任一点的应力和应变都不许超过材料的屈服应力和屈服应变。许用荷载法 2.理想弹塑性材料假设线性模型刚塑性模型理想弹塑性模型理想弹塑性材料假定：(1)材料的拉压性能相同(2)加载时，材料曲线分弹性I和塑性II两个阶段。(3)卸载时，卸载点在I、II两个阶段上是不同的。总之，材料加载时呈弹塑性，卸载时呈弹性。 §12-2极限弯矩和塑性铰纯弯曲矩形截面梁 1、弹性极限弯矩Ms在线弹性范围内，纯弯曲梁只受外力偶产生的弯矩，截面在变形后仍保持平截面，截面上的应变按截面高度线性分布，在中性轴处的应变等于零。按结构的弹性设计方法，当截面的最外层纤维达到材料的屈服应力，即此时达到截面的弹性极限状态。用M＝Ms矩形截面 线弹性状态弹塑性及塑性流动阶段 2、极限弯矩Mu当截面达到弹性极限状态外力偶继续增大M>Ms以后，截面上的应变分布仍与截面高度呈线性关系，即平截面假定仍然适用，见图14-2-1(c)。但截面上的应力分布不再与截面高度保持线性关系。(1)截面的弹塑性阶段(2)截面的塑性流动阶段矩形截面在塑性极限状态的极限弯矩(d) (3)塑性铰概念当截面出现并不断扩大塑性区进入弹塑性发展阶段，直到整个截面被塑性区充满的塑性极限状态止，截面上应变的发展始终与截面高度成线性关系。即尽管这一阶段塑性区上的应力停止在屈服应力值上，但应变仍与弹性核部分的应变分布斜直线共线发展。因此，当截面达到塑性极限状态时，比弹性极限状态的应变值显著增大，由此产生的是该截面两侧无限靠近的两个截面绕中性轴发生相对的转动的相对角位移效应。 塑性铰的以下特征：(1)塑性铰承受并传递极限弯矩Mu。(2)塑性铰是单向铰，只能使其两侧按与荷载增加（弯矩增大）相一致方向发生有限的转动。(3)塑性铰不是一个铰点，而是具有一定的长度。综上所述，截面上各点应力均等于屈服应力的应力状态、截面达到极限弯矩、截面形成塑性铰，均表示该截面达到其塑性流动的极限状态。 3.具有一个对称轴截面的极限弯矩(1)截面在塑性极限状态的中性轴位置截面上的应力应满足： 在塑性极限状态时截面上的轴力应满足：截面在塑性极限状态的中性轴平分截面总面积A，即为截面的等面积轴。上式只有在成立时才能满足，即受拉区的面积须等于受压区的面积。 (2)截面的极限弯矩Mu已知在塑性极限状态时截面的中性轴位置，可推导截面的极限弯矩如下。弯矩等于截面上应力对中性轴的合力矩，即：式中积分为截面的面积净矩，可写成：则极限弯矩可表示为： 弹性极限和塑性极限之间的弹塑性阶段，中性轴界于截面的形心轴和等面积轴之间。以上所讨论的是梁在纯弯受力和变形状态下的截面的两个阶段的极限状态和相应的极限弯矩。对非纯弯状态梁，通常剪力对梁的承载力的影响可忽略。所以仍可利用以上概念和结果。利用以上二式计算截面极限弯矩。 §12-2梁的极限荷载研究梁的极限荷载，是寻找能使梁结构达到塑性极限状态时的荷载值，也就是梁结构在丧失承载力之前所能承受的最大荷载值。在上一节讨论过的截面极限状态（极限弯矩）的基础上，本节讨论结构的极限状态（极限荷载）。 1.静定梁的极限荷载(a)(b)(c) (d)(e) (1).结构的极限状态极限荷载是相应于结构极限状态时的荷载。当MCMu。(b)(a) (c)可能机构I(d)可能极限弯矩图I (e)可能机构II(f)可能极限弯矩图II (g)可能机构III(h)不可能 当梁在极限状态下可能出现塑性铰的所有截面可预先判定，并可能的塑性铰的数目大于破坏机构需要的塑性铰数目时，可以得出按需要的塑性铰的数目的全部组合。假定每一种组合是一种可能得极限状态，即可按基本方法一一求得相应的可能得极限荷载。然后通过比较，其中最小荷载值既是梁得极限荷载。此中求极限荷载的方法可称作穷举法。 解：1)基本方法用破坏机构法可能机构I：(a)注意：在突变截面处的塑性铰的极限弯矩为较小极限弯矩。 可能机构II：由几何关系知：代入上式，得：(b) 可能机构III：(c) 当>，机构I为破坏机构。由式(b)知，当<<机构II为破坏机构。当=机构I、II都是相应的破坏机构。 图(d)、(f)、(h)是利用极限状态时可能的极限弯矩图由平衡条件进行计算的方法。由图(h)所示极限弯矩图的不可能将其排除。由图(f)分析可知，当<