机械设计基础 第2章 材料力学课件.ppt

第2章材料力学基础2.1材料力学的基本概念2.1.1构件的承载能力1.构件的承载能力：为了保证机械或结构在载荷作用下能正常工作，必须要求每个构件都具有足够的承受载荷的能力，简称承载能力。2.刚度：把构件抵抗变形的能力称为刚度。3.稳定性：杆件维持其原有平衡形式的能力称为稳定性。4.构件安全工作的三项基本要求：具有足够的强度、刚度和稳定性。2.1.2材料力学的任务材料力学的任务：为了解决安全性和经济性的矛盾，即研究构件在外力作用下的变形和失效的规律。保证构件既安全又经济的前提下，选用合适的材料，确定合理的截面形状和尺寸。 第2章材料力学基础2.1材料力学的基本概念2.1.3杆件变形的基本形式一、几个基本概念：1.杆：纵向尺寸（长度）远大于横向尺寸的材料，在材料力学上将这类构件称为。2.曲杆：杆的轴线为曲线的杆。3.直杆：杆的轴线为直线的杆。4.等横截面直杆：直杆且各横截面都相等的杆件。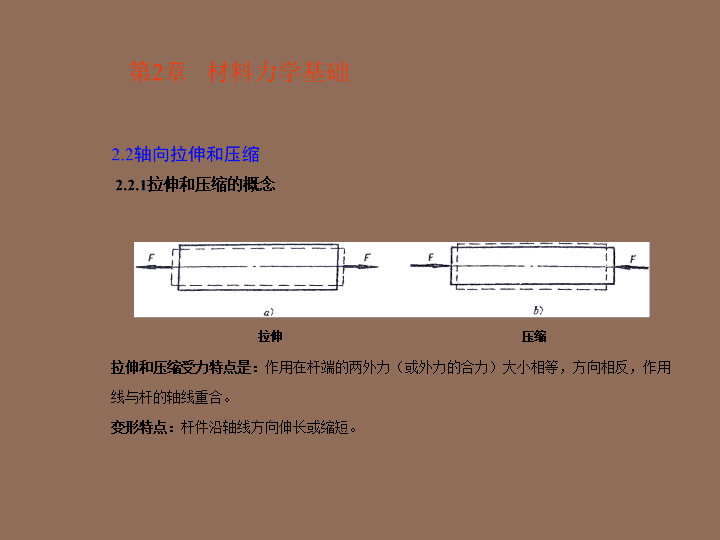二、杆件变形的基本形式（如右图所示） 第2章材料力学基础2.2轴向拉伸和压缩2.2.1拉伸和压缩的概念拉伸压缩拉伸和压缩受力特点是：作用在杆端的两外力（或外力的合力）大小相等，方向相反，作用线与杆的轴线重合。变形特点：杆件沿轴线方向伸长或缩短。 第2章材料力学基础2.2轴向拉伸和压缩2.2.2内力和截面法1.内力：杆件在外力作用下产生变形，其内部的一部分对另一部分的作用称为内力。2.轴力：拉压杆上的内力又称轴力。3.截面法：将受外力作用的杆件假想地切开来用以显示内力，并以平衡条件来确定其合力的方法，称为截面法。具体方法如右图所示：（1）截开沿欲求内力的截面，假想把杆件分成两部分。（2）代替取其中一部分为研究对象，画出其受力图。在截面上用内力代替移去部分对留下部分的作用。（3）平衡列出平衡方程，确定未知的内力。FX=0，得N-F=0故N=F 第2章材料力学基础2.2轴向拉伸和压缩2.2.2内力和截面法4.轴力符号的规定：拉伸时N为正（N的指向背离截面）；压缩时N为负（N的指向朝向截面）。【例2.1】一直杆受外力作用如下图所示，求此杆各段的轴力。2.2.3拉伸和压缩时横截面上的正应力1.应力：构件在外力作用下，单位面积上的内力称为应力。2.正应力：垂直于横截面上的应力，称为正应力。用σ表示。 第2章材料力学基础2.2轴向拉伸和压缩2.2.3拉伸和压缩时横截面上的正应力式中：σ——横截面上的正应力，单位MPa；N——横截面上的内力（轴力），单位N；A——横截面的面积，单位mm2。σ的符号规定与轴力相同。拉伸时，N为正，σ也为正，称为拉应力；压缩时N为负，σ也为负，称为压应力。【例2.2】截面为圆的阶梯形钢杆，如下图所示，已知其拉力P=40kN,d1=40mm,d2=20mm，试计算各段钢杆横截面上的正应力。 第2章材料力学基础2.2轴向拉伸和压缩2.2.4拉压变形和胡克定律（a）杆件受拉变形（b）杆件受压变形绝对变形：设等直杆的原长为L1，在轴向拉力（或压力）F的作用下，变形后的长度为L1，以△L来表示杆沿轴向的伸长（或缩短）量，则有△L=L1－L，△L称为杆件的绝对变形。相对变形：绝对变形与杆的原长有关，为了消除杆件原长度的影响，采用单位原长度的变形量来度量杆件的变化程度，称为相对变形。用ε表示,则=△L/L=（L1－L）/L胡克定律：当杆内的轴力N不超过某一限度时,杆的绝对变形△L与轴力N及杆长L成正比,与杆的横截面积A成反比.这一关系称为胡克定律,即△LNL/A引进弹性模量E,则有△L=NL/AE也可表达为：=E此式中胡克定律的又一表达形式，可以表述为：当应力不超过某一极限时，应力与应变成正比。 第2章材料力学基础2.2轴向拉伸和压缩2.2.5拉伸（压缩）时材料的力学性质图1.低碳钢拉伸变形σ—ε曲线图2.灰铸铁拉伸变形σ—ε曲线1.低碳钢拉伸变形过程如图1所示低碳钢拉伸变形过程如图1.所示可分为四个阶段：①弹性阶段②屈服阶段③强化阶段④颈缩阶段2.灰铸铁拉伸变形过程如图2所示 第2章材料力学基础2.2轴向拉伸和压缩2.2.5拉伸（压缩）时材料的力学性质低碳钢压缩时的σ—ε曲线铸铁压缩时的σ—ε曲线从图中可以看出，低碳钢压缩时的弹性模量与拉伸时相同，但由于塑性材料，所以试件愈压愈扁，可以产生很大的塑性变形而不破坏，因而没有抗压强度极限。从图中可以看出，铸铁在压缩时其线性阶段不明显，强度极限σb比拉伸时高2~4倍，破坏突然发生，断口与轴线大致成45°~55°的倾角。由于脆性材料抗压强度高，宜用于制作承压构件。 第2章材料力学基础2.2轴向拉伸和压缩2.2.6许用应力和安全系数许用应力：在强度计算中，把材料的极限应力除以一个大于1的系数n（称为安全系数），作为构件工作时所允许的最大应力，称为材料的许用应力。用表示。s=s/nb=b/n式中，n为安全系数。它反映了构件必要的强度储备。在工程实际中，静载时塑性材料一般取n=1.2~2.5；对脆性材料一般取n=2~3.5。安全系数也反映了经济与安全之间的矛盾关系。取值过大，许用应力过低，造成材料浪费。反之，取值过小，安全得不到保证。塑性材料一般取屈服点σs作为极限应力；脆性材料取强度极限σb作为极限应力。 第2章材料力学基础2.2轴向拉伸和压缩2.2.7构件在拉伸和压缩时的强度校核N/A利用强度条件可解决工程中的三类强度计算问题：1.强度校核N/A2.选择截面尺寸AN/3.确定许可载荷N/A【例2.3】如右图所示为铸造车间吊运铁水包的双套吊钩。吊钩杆部横截面为矩形。b=25mm，h=50mm。杆部材料的许用应力=50MPa。铁水包自重8kN，最多能容30kN重的铁水。试校核吊杆的强度。 第2章材料力学基础2.3剪切与挤压2.3.1剪切1.剪切面：在承受剪切的构件中，发生相对错动的截面，称为剪切面。2.剪切变形的受力特点是：作用于构件两侧面上外力的合力大小相等，方向相反，且作用线相距很近。3.剪切变形的特征是：构件的两个力作用线之间的部分相对错动。4.剪力：在剪切面m-n上,必存在一个大小相等而方向与F相反的内力Q,称为剪力。=Q/A式中：——切应力，单位MPa；Q——剪切面上的剪力，单位N；A——剪切面积，单位mm2。 第2章材料力学基础2.3剪切与挤压2.3.2挤压1.挤压:机械中受剪切作用的联接件，在传力的接触面上，由于局部承受较大的压力，而出现塑性变形，这种现象称为挤压。如图下a所示2.挤压面:构件上产生挤压变形的表面称为挤压面。如图下b所示（ａ）　　　　　　　　　　　（ｂ）3.挤压应力:挤压作用引起的应力称为挤压应力，用符号σｊｙ表示。挤压应力在挤压面上的分布也很复杂，工程中近似认为挤压应力在挤压面上均匀分布。则σｊｙ＝Ｐ／Ａｊｙ 第2章材料力学基础2.3剪切与挤压2.3.３剪切和挤压强度条件1.抗剪强度：剪切面上最大切应力，即抗剪强度τmax不得超过材料的许用切应力，表示成为τmax＝Ｑ／Ａ≤[τ]２.挤压强度：挤压面上的最大挤压应力不得超过挤压许用应力，即σｊｙｍａｘ＝Ｐ／Ａｊｙ≤[σｊｙ]提示：利用抗剪强度和挤压强度两个条件可解决三类强度问题，即强度校核，设计截面尺寸和确定许用载荷。2.3.4剪切和挤压在生产实践中的应用【例2.4】如下图所示，已知钢板厚度t=10mm，其剪切极限应力为[τ]=300MPa，若用冲床在钢板上冲出直径d=25mm的孔，问需多大的冲剪力P？ 第2章材料力学基础2.3剪切与挤压2.3.4剪切和挤压在生产实践中的应用【例2.5】如下图表示齿轮用平键与轴联接，已知轴的直径d=70mm，键的尺寸为ｂ×ｈ×Ｌ２０mm×１２mm×１０mm，传递的转距m=2kＮ·m，键的许用应力[τ]=60MPa，[σｊｙ]=100MPa，试校核键的强度。 第2章材料力学基础2.3剪切与挤压2.3.4剪切和挤压在生产实践中的应用【例2.6】如下图所示的起重机吊钩，上端用销钉联接。已知最大起重量F=120kN，联接处钢板厚度t=15mm，销钉的许用剪应力[τ]=60MPa，许用挤压应力[σjy]=180MPa，试计算销钉的直径d。