材料力学课件-复习

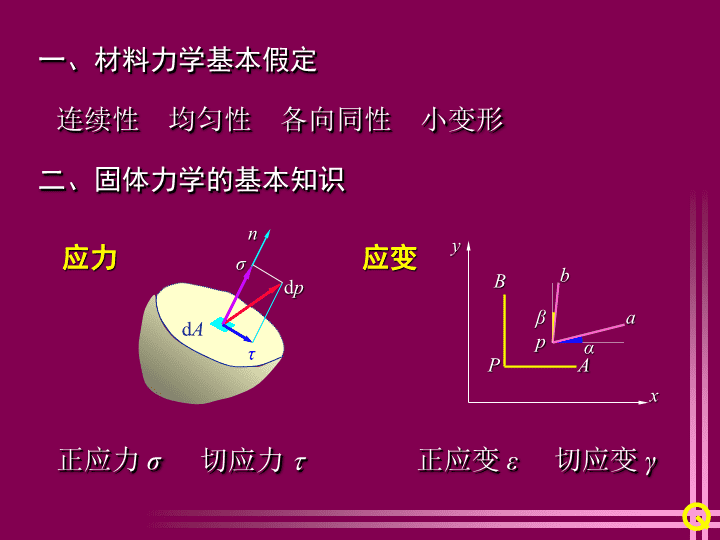
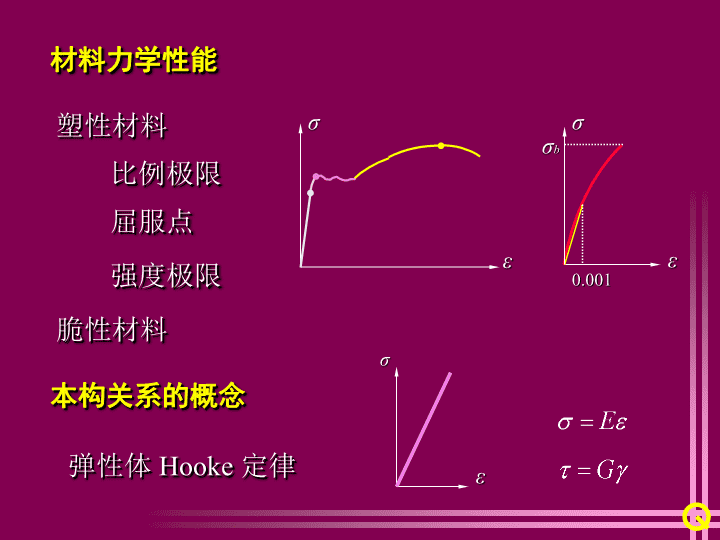
材料力学主要内容复习 一、材料力学基本假定连续性均匀性各向同性小变形二、固体力学的基本知识dAndpστ正应力σ切应力PABxypabαβ正应变ε切应变γ应力应变 塑性材料脆性材料εσ比例极限屈服点强度极限εσσb0.001材料力学性能本构关系的概念弹性体Hooke定律εσ E和v的意义单位取值范围E,G和v间的关系弹塑性体的本构模型σεεs 三、截面的几何性质静矩惯性矩惯性积极惯性矩组合图形静矩的计算形心的计算方法AxSAyd=AySAxd=AxScy=AyScx= 常用图形的惯性矩平行移轴公式DxyDxydhbyxyxccbay’x’3121hbIy=—4321DIpp=—4641DIIyxp==— 四、杆件的内力轴力、扭矩、剪力、弯矩的意义符号规定用截面法求内力刚架内力图根据外荷载画剪力弯矩图梁的平衡微分方程主惯性矩、形心主惯性矩的概念 五、杆件横截面上的应力及强度拉压杆正应力圆轴扭转切应力最大切应力 梁弯曲正应力最大正应力梁弯曲切应力 k=3/2k=4/3k=2k=1最大弯曲切应力简易计算式 组合变形的应力拉弯组合拉弯组合中的最大正应力 弯扭组合组合变形中危险点的确定弯曲正应力扭转切应力PLadPLadPTPLaABdPT 六、杆件的变形桁架结点位移的计算拉压杆的伸长量圆轴扭转时两端面的相对转角A’AA梁的挠度转角挠度微分方程 积分法求梁的变形集中力均布荷载力偶矩Paaq0am固定端处位移为零，转角为零。简支端处位移为零。 叠加法计算梁的挠度和转角mPAqAmAPABqABmAB 七、超静定问题拉压和扭转超静定问题弯曲超静定平衡方程物理方程协调方程静定基和多余约束力协调方程vqRvRqLBqB 八、应力和应变理论斜截面上的应力σyσxτxynσyσxτxyαnσyσxτxyσαnτασyσxτxynτασyσxτxyσα主方向、主应力的概念及计算最大切应力 应变理论与应力理论的相似性广义Hooke定律体积变化率应变片直角应变花等角应变花 九、强度理论四个强度理的等效应力拉弯扭组合情况下第三、第四强度准则的应用圆轴弯扭组合情况下第三、第四强度准则的应用 lEIPlEIPlEIPPlEIμ=1μ=0.7μ=0.5μ=2十一、稳定理想压杆的临界荷载柔度概念临界应力 ㊀㊀例qa2qaaqa2ABRBRAqa2qaaqa2AB2qa4qa2qa3qaqaqa23qa/22qa2 例求图形的面积、形心的x坐标和对x轴的惯性矩。xyy=xnhb 例求图形的面积、形心的x坐标和对x轴的惯性矩。xyy=xnhb dx例若梁中存在分布力偶矩m，导出梁的微分方程。力平衡力矩平衡qQQ+dQMmM+dM P2L/3L/3L/2L/2AB2EAEAR1R2例求图示AB间的相对位移。平衡条件物理条件协调条件轴力AB间的相对位移设左右两端反力分别为R1和R2，则两段内的轴力 EAEAaaa45°①②P例图示横梁为刚性杆，求两根杆件中的内力。平衡方程物理方程协调方程vBΔa2Δa1设两杆内力分别为拉力N1和压力N2，两杆在横梁上的作用力分别为R1和R2，则有拉力压力PR1R2 D2d2d1D1例两根等长度的钢管松套在一起。当内管受扭矩T作用时，将两管的两端焊接起来，然后去掉扭矩。此时两管内横截面上的最大切应力各为多少？试画出横截面上的应力分布图。D1=100d1=90D2=90d2=80T=2kNmφφφφφ1φφ2φφ φ1φφ2D2d2d1D1D1=100d1=90D2=90d2=80T=2kNm协调方程平衡方程物理方程 φ1φφ2 例在横截面如图的梁中，许用拉应力是许用压应力的一半，如何选用尺寸b，使梁在保证经济性的前提下使许用荷载最大？要使梁的许用荷载最大，应满足202080byc取b=92mm AALL/2L/2PAEIEIP/2P/2例求图示结构中集中力作用点的竖向位移A aa/4EIAa/4PFFAPAPFF例如图的结构中所加的一对力F为多大时可使A点的挠度为零？APFFAPF aa/4EIAa/4PFFAFθCCvAAAFv2AFθ’CCvBABAPv1 aa/4EIAa/4PFFPFF1Pa/4Fa/4Fa/4a/4 aaCEIδ例图中梁中点C发生支座沉陷δ，求由此而引起的最大正应力。hbaaCEIδP此处支座沉陷所引起的应力，相当于集中力作用在中点引起的应力。 例图示结构下方贴有两个应变片，若材料E=50GPa，v=0.3，求两个应变片a和b的理论读数。长孔区域构成拉弯组合变形拉伸计算以上沿为基准计算形心位置P=3kNab301010101040101010yc2055 弯曲计算惯性矩计算应变片读数3010101010728205C3010101010y2=27y1=33CP=3kNab组合变形 例悬臂梁上沿承受切向均布荷载t，已知E，求A点的竖向位移和横向位移。将切向荷载向轴线平移，产生分布力偶矩LAbhxyxMNx 例悬臂梁上沿承受切向均布荷载t，已知E，求A点的竖向位移和横向位移。LAbhxMNx L/2L/2PBCPBCm例画出如图结构的剪力弯矩图。结构为超静定的，选如图的静定基：5P/1611P/165P/1611P/165PL/323PL/16 L/2L/2PaABCkPABCFPABCFm例图示梁B处为刚结点，AB可视为刚体，A处弹簧刚度为k，求B处弯矩。PABCkθBΔx PvPBRvR1aPaAB例画出图示结构的内力图。RvR2mPR选择如图的静定基 aPaAB5Pa/8P3P/83P/83P/8NP3P/8Q5Pa/83Pa/8M例画出图示结构的内力图。 例求应变片的理论读数。E=200GPaL=1000b=30h=80q=50kN/mν=0.3该处弯矩正应力该处剪力切应力LL/3qbhh/4abcqL/2 应力状态应变状态故有LL/3qbhh/4abc L=600F=2kNa=150d=40ABC例用第四强度理论校核结构强度，AB段可视为刚体。结构可简化为如图的结构，这是一个一次超静定问题。解除A处约束，代之以约束反力R协调条件故有LFadACBLFaRACBdFACBRACBRACBRACBLFadACB 结构的危险点在C截面的上下两点，其应力状态如图τσ故结构安全。LFaRACBd xyzPaaLAxyzP/2aLX1xyX1=1M=1T=1z1aLxyzP/2Pa/2aLPL/2Pa/2例图中的折杆均为直径是d的圆杆，求A处的支反力。在P力作用点处将折杆切开，由于对称性，该截面处只存在弯矩，令其为X1，便有 xyzP/2aLX1支反力偶矩方向如图。xyzP/2aLX1 aEIFaaEI例计算结构中弹簧的变形量。aEIFaaEIX1X2aX1=1aX2=1a将右边铰支座和弹簧的作用分别转为X2和X1 aEIFaaEIX1X2aX1=1aX2=1aFa正则方程 aEIFaaEIX1X2aX1=1aX2=1aFa弹簧压缩量 aaaa/2a/2a1/21/21例结构各部抗弯刚度均为EI，画出如图结构的弯矩图。aaaX1X2X1X2解除顶部约束，可排除竖直方向支反力。 X1X2a/2a/2a1/21/21 X1X2qa2/10qa2/40qa2/40qa2/20qa2/1011qa/20qa/40qa/409qa/20支反力弯矩图