材料力学课件xt7压杆稳定

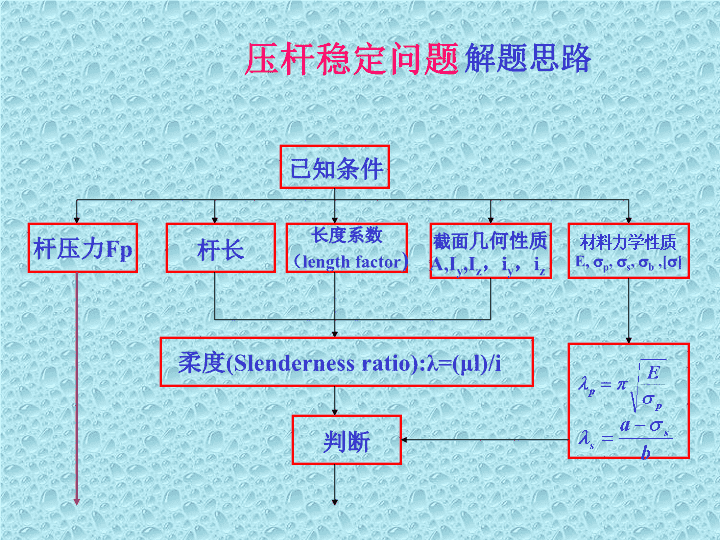
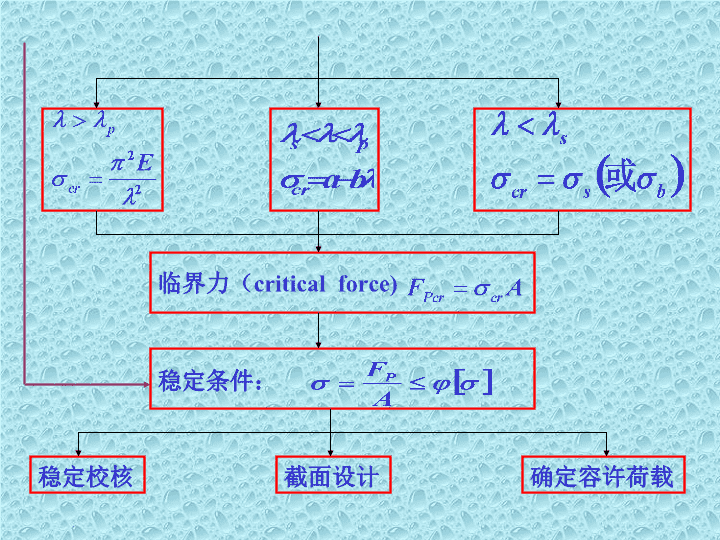
压杆稳定问题解题思路已知条件杆压力Fp杆长长度系数（lengthfactor)截面几何性质A,Iy,Iz，iy，iz材料力学性质E,p,s,b,[]柔度(Slendernessratio):λ=(μl)/i判断 临界力（criticalforce)稳定条件：稳定校核截面设计确定容许荷载 (a)(b)(c)(d)(e)(f)相当长度越大临界力越小∴临界力排序为：[7-1]图示各杆材料和截面均相同，试问杆能承受的压力哪根最大，哪根最小（图f所示杆在中间支承处不能转动）？ 【7-2】长5m的10号工字钢，在温度为0℃时安装在两个固定支座之间，这时杆不受力。已知钢的线膨胀系数l=125×10-7℃-1,E=210GPa。试问当温度升高至多少度时，杆将丧失稳定性？【解】 【7-3】图示结构中，BC为圆截面杆，其直径d=80mm,AC为边长a=70mm的正方形截面杆。已知该结构的约束情况为A端固定，B、C为球形铰。两杆的材料均为Q235钢，弹性模量E=210GPa,，可各自独立发生弯曲互不影响。若结构的稳定安全系数nst=2.5，试求所能承受的许可压力。解：BC段为两端铰支，=1 AB杆为一端固定，一端铰支，故 【7-4】图示结构中杆AC与CD均由Q235钢制成，C，D两处均为球铰。已知d=20mm,b=100mm,h=100mm,E=210GPa,s=235MPa,b=400MPa,强度安全因数n=2.0,稳定安全因数ns=3.0。试确定该结构的许可荷载。mm；，，解：（1）杆CD受压力梁BC中最大弯矩（2）梁BC中 （3）杆CD=（由梁力矩平衡得）故，由（2）、（3）可知，（Q235钢的p=100) 【7-5】图示结构ABCD由三根直径均为的圆截面钢杆组成，在B点铰支，而在A点和C点固定，D为铰接点，l/d=10。若结构由于杆件在平面ABCD内弹性失稳而丧失承载能力，试确定作用于结点D处的荷载F的临界值。【解】此结构为超静定结构，当杆DB失稳时结构仍能继续承载，直到杆AD及DC也失稳时整个结构才丧失承载能力，故 【7-6】图示铰接杆系ABC由两根具有相同截面和同样材料的细长杆所组成。若由于杆件在平面ABC内失稳而引起毁坏，试确定荷载F为最大时的角（假设0<</2）。【解】由B点的平衡条件：当两杆同时达到临界值时，FP最大。 【7-7】图示连杆，其约束情况是：在xy平面内弯曲时是两端铰支，在xz平面内弯曲时是两端固支，材料的弹性模量E＝200GPa，p=100。试求该杆的临界力Pcr。 解：设连杆在xy面内失稳，两端为铰支，长度系数＝1，此时截面以z轴为中性轴，惯性半径及长细比是故是大柔度杆。 设在xz平面内失稳，两端为固支，长度系数＝0.5，此时截面以y轴为中性轴，惯性半径及长细比是：，也是大柔度杆。因z>y，失稳发生在xy平面。所以 故此杆的临界力为Pcr=119.26kN。解题指导:压杆的临界力与其刚度及约束有关，当杆在不同平面内有不同的刚度和约束时，必须比较杆在两个失稳平面内的柔度，由柔度大的确定临界力，也可以求出杆在两个面内的临界力，其中较小者才是该杆的临界荷载。 【例】图示立柱由两根10槽钢组成，上端为球形铰支，下端为固定，长度l=6m，材料的弹性模量E=200GPa，比例极限sp=200MPa，试问当a为何值时该立柱临界荷载最大，并求此临界荷载。 (1)计算P(2)查表，得槽钢的截面几何性质：截面惯性矩：Iy=198.3cm4，Iz0=26cm4惯性半径：iy=3.95cm，iz0=1.41cm，面积A=12.74cm2，槽钢截面形心Z0到直边的距离y0=1.52cm。（3）计算在xz平面失稳的柔度y为大柔度杆。(4)计算距离a。注意到当Iy=Iz时，Pcr有最大值 Iy=2×198.3=396.6cm4Iz=2×[(Iz0+A×(y0+a/2)2)=2×[26+12.74×(1.52+a/2)2]令Iy=Iz，解得a=4.32cm（5）计算Pcr解题指导；在截面积不变的情况下，压杆在xy和xz两平面内失稳的临界力相等时，承受的临界力最大。当各方向的约束相同时，只需使Iy＝Iz即可。