绕定轴转动刚体的轴承动反力（重庆大学理论力学课件）.ppt

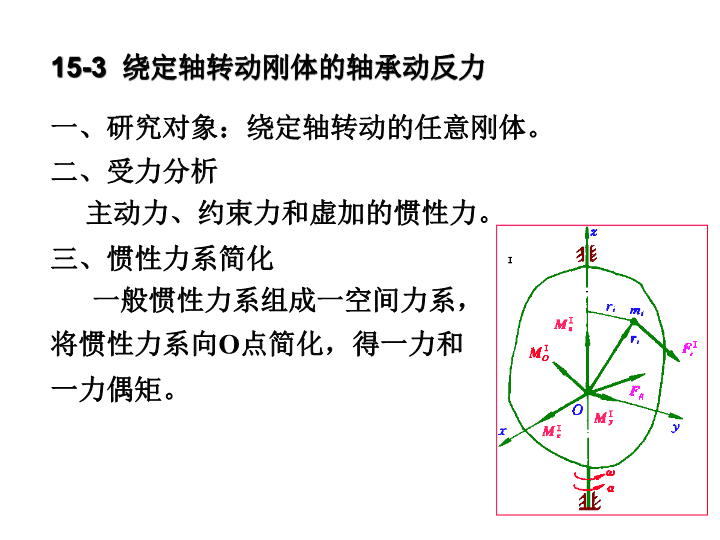
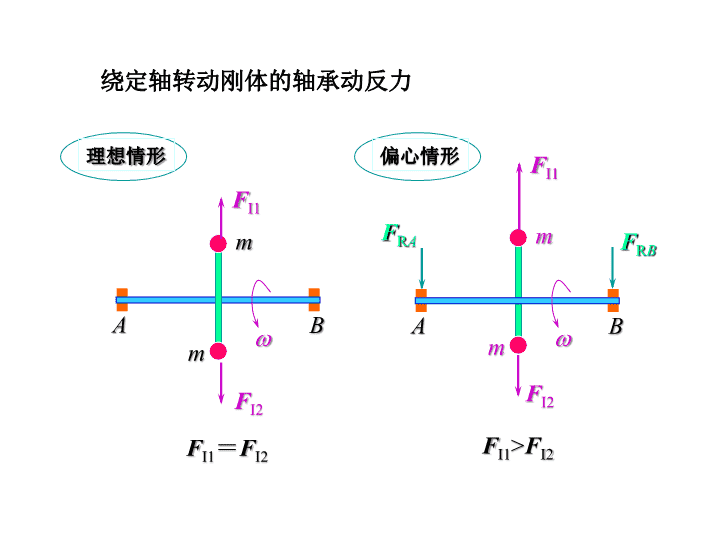
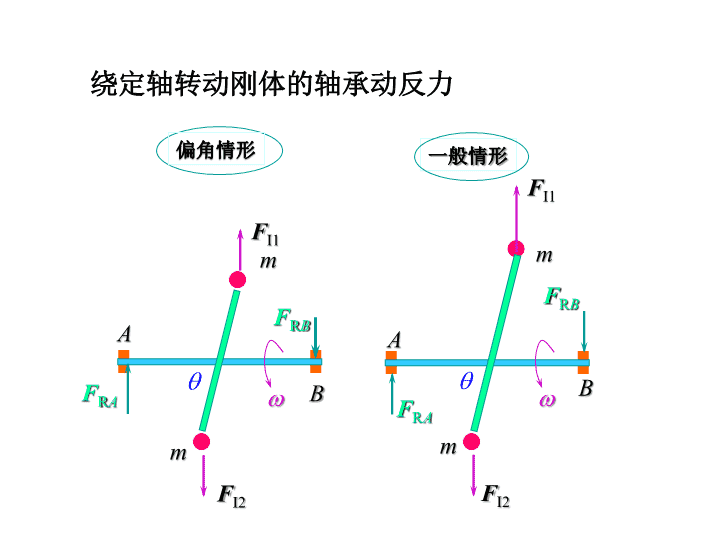
15-3绕定轴转动刚体的轴承动反力一、研究对象：绕定轴转动的任意刚体。二、受力分析主动力、约束力和虚加的惯性力。三、惯性力系简化一般惯性力系组成一空间力系，将惯性力系向O点简化，得一力和一力偶矩。 mmABABmmFI1FI2FI1FI2FI1＝FI2FI1>FI2FRAFRB理想情形偏心情形绕定轴转动刚体的轴承动反力 ABmmABmmFI1FI2FI1FI2FRBFRAFRAFRB偏角情形绕定轴转动刚体的轴承动反力一般情形 三、惯性力系简化一般惯性力系组成一空间力系，将惯性力系向O点简化，得一力和一力偶矩。这个力等于惯性力系的主矢量，这个力偶的矩等于惯性力系对O点的主矩。即 由于定轴转动刚体内各点的加速度皆与转轴垂直，因而FI垂直于转轴。为了求惯性力系对O点的主矩，将速度和加速度写成矢量积的形式 式中 质量对称面式中为刚体对z轴的转动惯量；为刚体对z轴的两个离心转动惯量或惯性积。 根据力矩关系定理，得惯性力系对各坐标轴的主矩分别为 惯性力系对于转轴z的惯性力矩为惯性力系对固结于刚体并垂直于转轴的x、y两轴的惯性力矩分别为 四、平衡方程为了转动刚体支座反力，将此主动力系也向O点简化，如图所示 由前五个方程解得轴承反力：由于惯性力系分布在垂直于转轴的各平面内，沿z轴的反力与惯性力无关。 由式可知，由于惯性力系分布在垂直于转轴的各平面内，沿z轴的反力与惯性力无关。与z轴垂直的轴承反力由两部分组成：（1）有主动力引起的静反力；（2）由惯性力引起的附加动反力。 即轴承附加动反力等于零的条件是：惯性力系的主矢量等于零，惯性力系对于x轴和y轴的矩等于零。 轴承附加动反力等于零的条件是：惯性力系的主矢量等于零，惯性力系对于x轴和y轴的矩等于零。由前面的推导，应有要使惯性力系的主矢等于零，必须aC=0，即转轴通过质心。要使主矩等于零，必须有Jxz=Jyz=0，即刚体对转轴z的惯性积等于零。 五、讨论1、静反力：由主动力引起，与运动无关。2、动反力：①起因：质心C不在转轴上②危害性：将要产生动反力。③消除附加动反力的方法；对于高速转动部件的机器或机械，附加动反力将可能会很大，应设法减小或消除，以免产生弯曲、断裂等不良后果。 绕定轴转动刚体的轴承动反力：（1）动反力:在工程实际中，由于高速转子绕定轴转动时产生的作用于轴承上的附加力，称为动反力，动反力往往很大，以至使机器零件破坏或引起振动。（2）产生原因：①质心C不在转轴上时：如图所示：两质量相等的小球m1和m2，绕铅垂直轴匀速转动，如果两球的中心连线与转轴相垂直，且质心C在轴线上，则： mmABABmmFI1FI2FI1FI2FI1＝FI2FI1>FI2FRAFRB理想情形偏心情形绕定轴转动刚体的轴承动反力 ABmmABmmFI1FI2FI1FI2FRBFRAFRAFRB偏角情形绕定轴转动刚体的轴承动反力一般情形 六、动平衡的概念1、定义：如一刚体，在主动力、约束力及附加惯性力的作用下处于平衡，则称之为动平衡状态。七、惯性主轴2、条件：惯性力系为平衡力系。3、对转轴的要求：①转轴要过质心（xc=yc=0）；②Jyz=Jxz=0(即转轴为惯性主轴) 惯性主轴与中心惯性主轴：(1)惯性主轴：即：如果刚体对通过点O的z轴的惯性积：则z轴称为该点的惯性主轴。（2）中心惯性主轴：过质心的惯性主轴称为中心惯性主轴。故避免出现轴承动反力的条件是：刚体的转轴应取刚体的中心惯性主轴。 上述结论也可叙述为：刚体绕定轴转动时，避免出现轴承动反力的条件是：转轴通过刚体的质心，且刚体对转轴的惯性积等于零，即转动轴必须是刚体的中心惯性主轴。 4静平衡与动平衡：静平衡：如果转动刚体的转轴通过刚体的质心，刚体除受重力外，没有受到其它主动力作用，刚体可以在任意位置平衡的现象称为静平衡；动平衡：如果转动轴是中心惯性主轴，刚体绕定轴转动时，不出现轴承动附加反力的现象称为动平衡。 静平衡：（a)(b)、(d)动平衡：(a)动平衡的刚体，一定是静平衡的；反过来，静平衡的刚体，不一定是动平衡的。[例5]质量不计的刚轴以角速度匀速转动，其上固结着两个质量均为m的小球A和B。指出在图示各种情况下，哪些是静平衡的？哪些是动平衡的？ 例:如图所示的飞轮，质量为m=200kg，其质心C至转轴的距离e=0.05cm，飞轮安装在转轴的中点。若飞轮以匀转速n=6000r/min绕其轴转动，试求飞轮质心C运动到最低位置时轴承反力。解：以飞轮和转轴所组成的质点系为研究对象，作用于其上的力有：重力mg和轴承反力FA、FB。 解：作用于其上的力有：重力mg和轴承反力FA、FBRI＝mew2。又RI的方向随质心位置而异，当质心C运动到如图所示的最低位置时，RI铅垂向下。因飞轮转速不变，附加于飞轮上的惯性力系向轴心O简化后所得的主矩应为零，故简化结果为合力RI，且 因飞轮位于转轴的中点，故由平衡方程得由此可见，轴承反力为两项之和:前者为飞轮自重引起的静反力，后者为飞轮作偏心运动时所引起的附加动反力。本例中，附加动反力约为静反力的20倍FA＝FB＝（mg＋mew2）/2m=200kg，e=0.05cm，n=6000r/min＝200×［9.8＋0.0005×(6000p/30)2］/2＝980＋19720＝20700N 动反力有时会造成很大危害。在设计中虽力图使质心位于转轴上，但由于设计、制造和安装时很难完全避免的误差，必然会导致转动物体的质心偏离转轴。因此，高速转动物体的动反力可以达到很大的值。所以，必须用实验方法对高速转动的物体加以平衡校正，务必使它在转动时的动反力被限制在容许的范围之内。 加平衡质量 根据达朗伯原理，以静力学平衡方程的形式来建立动力学方程的方法，称为动静法。应用动静法既可求运动，例如加速度、角加速度；也可以求力，并且多用于已知运动，求质点系运动时的动约束反力。应用动静法可以利用静力学建立平衡方程的一切形式上的便利。例如，矩心可以任意选取，二矩式，三矩式等等。因此当问题中有多个约束反力时，应用动静法求解它们时就方便得多。达朗贝尔原理的应用 ①选取研究对象。原则与静力学相同。②受力分析。画出全部主动力和外约束反力。③运动分析。主要是刚体质心加速度，刚体角加速度，标出方向。应用动静法求动力学问题的步骤及要点：④虚加惯性力。在受力图上画上惯性力和惯性力偶，一定要在正确进行运动分析的基础上。熟记刚体惯性力系的简化结果。 ⑤列动静方程。选取适当的矩心和投影轴。⑥建立补充方程。运动学补充方程（运动量之间的关系）。⑦求解求知量。[注]的方向及转向如已在受力图中标出，建立方程时，只需按代入即可。 例1质量为m1和m2的两重物，分别挂在两条绳子上，绳又分别绕在半径为r1和r2并装在同一轴的两鼓轮上，已知两鼓轮对于转轴O的转动惯量为J，系统在重力作用下发生运动，求鼓轮的角加速度。取系统为研究对象解：用达朗伯原理求解虚加惯性力和惯性力偶： 由动静法：列补充方程：代入上式得： ABCcbh汽车连同货物的总质量是m，其质心C离前后轮的水平距离分别是b和c，离地面的高度是h。当汽车以加速度a沿水平道路行驶时，求地面给前、后轮的铅直反力。轮子的质量不计。[例5] ABCcbhFIaFBmgFNAFNB取汽车连同货物为研究对象。汽车实际受到的外力有：重力mg，地面对前、后轮的铅直反力FNA，FNB以及水平摩擦力FB(注意：前轮一般是被动轮，当忽略轮子质量时，其摩擦力可以不计)。解：因汽车作平动，其惯性力系合成为作用在质心C上的一个力F*=Ma。于是可写出汽车的动态平衡方程 汽车的动态平衡方程由式(1)和(2)解得ABCcbhFIaFBmgFNAFNBFI=Ma 例2在图示机构中，沿斜面向上作纯滚动的圆柱体和鼓轮O均为均质物体，各重为P1和P2，半径均为R，绳子不可伸长，其质量不计，斜面倾角q，如在鼓轮上作用一常力偶矩M，试求：(1)鼓轮的角加速度？(2)绳子的拉力？(3)轴承O处的支反力？(4)圆柱体与斜面间的摩擦力（不计滚动摩擦）？ 解：用达朗贝尔原理求解取轮O为研究对象，虚加惯性力偶列出动静方程：取轮A为研究对象，虚加惯性力和惯性力偶MIA如图示。 列出动静方程：运动学关系：取轮O为研究对象，取轮A为研究对象， 运动学关系：，将MI，FI，MIA及运动学关系代入到(1)和(4)式并联立求解得： 代入(2)、(3)、(5)式，得： 均质圆盘质量为mA，半径为r。细长杆长l=2r，质量为m。杆端A点与轮心为光滑铰接，如图所示。如在A处加一水平拉力F，使轮沿水平面滚动。问F力多大能使杆的B端刚刚离开地面？又为保证纯滚动，轮与地面间的静滑动摩擦系数应为多大？mAgmgFABC例10 细杆刚离地面时仍为平动，而地面约束力为零，设其加速度为a。以杆为研究对象，杆承受的力并加上惯性力如图所示，其中F*IC=maC=ma。解出ABCFICmgFAxFAya解：按动静法列出方程mAgmgFABC 为求摩擦力，应以圆轮为研究对象。由方程，得地面摩擦力解得mAgmgFABCFNFIAFICMIFSmAgFAFNFIAMIFs整个系统承受的力并加上惯性力如图，其中由方程得 再以整个系统为研究对象，由方程，得由此，地面摩擦系数mAgmgFABCFNFIAFICMIFsmAgFAFNFIAMIFs 设匀质转子重P，质心C到转轴的距离是e，转子以匀角速度ω绕水平轴转动，AO=a，OB=b(图a)。假定转轴与转子的对称平面垂直，求当质心C转到最低位置时轴承所受的压力。baezCOBA(a)例6 解:轴Oz是转子在点O的主轴之一。可见惯性力对点O的主矩在垂直于Oz的平面上两轴的投影MICx和MICy恒等于零。方向沿OC。当质心C转到最低位置时，轴上实际所受的力如图b所示。(a)baezCOBAbaezCOBA(b)PFBFA又a=0，这样MICz也等于零。因此转子的惯性力合成为作用于点O的一个力FIC，大小等于 根据动静法写平衡方程由式(1)和(2)解得两轴承所受的力分别和FA，FB的大小相等而方向相反。baezCOBA(b)PFBFA 解：刚体作平面运动，惯性力系向质心简化，例习题12-29：均质杆AB长为l，质量为m，其中自铅直位置开始A端沿墙壁向下滑动，B端沿水平面滑动，AB保持在铅直平面内。不计摩擦，求杆AB任一瞬时的角速度和角加速度用位置角q表示。 对时间求二阶导数，得由动静法 代入数据得：分离变量积分得 解法二；用动能定理求解。任一瞬时系统的动能其中vC＝lw/2由动能定理得 由动能定理得解得对上式导数得 解法三；用刚体平面运动微分方程求解。解法四：可将惯性力投影的自然轴上，质心C的轨迹曲率中心不一定是瞬心I点，但利用动静法对I点取矩时，法向惯性力通过矩心而不出现。 MCI＝JCa；MCI＝ml2a/12FnI（作用线沿对角线OI）FtI＝mla／2又解：1、惯性力系向质心简化得（当质心到速度瞬心的距离保持不变时，可对瞬心取动量矩）∑MI＝0FtIl／2＋MCI―mglsinq／2＝0整理上式得a＝3gsinq／2l