哈工大理论力学课件第八章.ppt

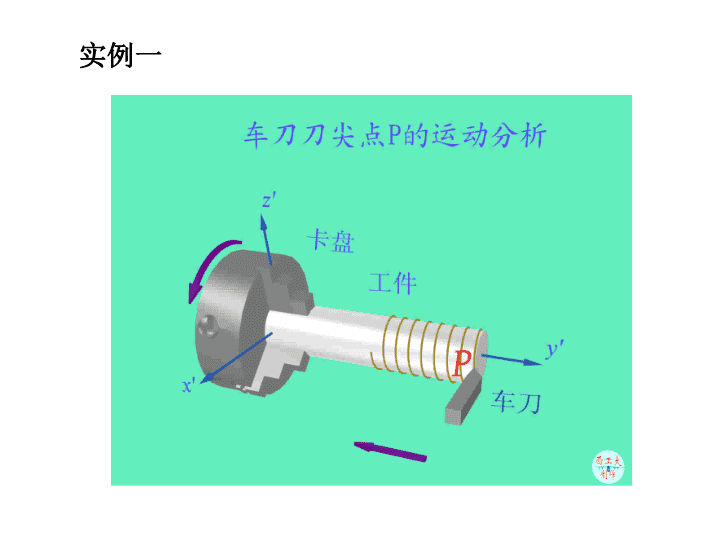
第八章点的合成运动 实例一 §8-1　相对运动·牵连运动·绝对运动两个坐标系定坐标系（定系）动坐标系（动系）三种运动绝对运动：动点相对于定系的运动。相对运动：动点相对于动系的运动。牵连运动：动系相对于定系的运动。 实例二 实例三 绝对运动1.绝对运动方程2.绝对运动轨迹3.绝对速度点M相对于定系Oxy的运动 相对运动1.相对运动方程2.相对运动轨迹3.相对速度点M相对于动系O’x’y’的运动 牵连运动1.平移2.定轴转动动系相对于定系的运动 例8-1已知OP=x=asint,=t.求刀尖P在工件上划出的痕迹 解.1.动点=P动系=工件=Ox’y’2.相对运动方程x’=OPcost=asintcost=(asin2t)/2y’=OPsint=asin2t=a(1-cos2t)/2相对运动轨迹(x’)2+(y’-a/2)2=a2/4 例8-2点M相对于动系沿半径为r的圆周以速度v作匀速圆周运动(圆心为O1），动系　　相对于定系　　以匀角速度ω绕点O作定轴转动，如图所示。初始时　与　　重合，点M与O重合。求：点M的绝对运动方程。 解:相对运动方程代入动点：点动系：绝对运动方程 牵连点的运动zxyOzxyP，P1P绝对运动相对运动P1§8-2　点的速度合成定理 r=r’+r1速度合成公式zxyrr1r’P，P1PP1 定系:Oxyr=r(t)动系:O’x’y’r’=r’(t)=x’i’+y’j’r=R+r’=R+x’i’+y’j’速度合成公式的严格理论推导 r=R+r’=R+x’i’+y’j’绝对速度va=dr/dt=idx/dt+jdy/dt相对速度vr=i’dx’/dt+j’dy’/dt 例8-3平面曲柄推杆机构如图所示，推杆BC可沿导轨上下移动，曲柄OA=l，绕轴O转动的角速度为ω，求当OA与铅垂线成夹角φ时，推杆的速度。 解:1.动点=滑块A，动系=推杆BC2。分析三种运动绝对运动:圆周运动相对运动:直线运动牵连运动:平移Va=Ve+Vr3。速度合成公式大小l??方向 例8-4　刨床的急回机构如图所示。曲柄OA的一端A与滑块用铰链连接。当曲柄OA以匀角速度ω绕固定轴O转动时，滑块在摇杆O1B上滑动，并带动杆O1B绕定轴O1摆动。设曲柄长为OA=r，两轴间距离OO1=l。求：曲柄在水平位置时摇杆的角速度。 2、运动分析：绝对运动－绕O点的圆周运动；相对运动－沿O1B的直线运动；牵连运动－绕O1轴定轴转动。解:1、动点：滑块A动系：摇杆3、大小方向√　√　√ 例8-5如图所示半径为R、偏心距为e的凸轮，以角速度ω绕O轴转动，杆AB能在滑槽中上下平移，杆的端点A始终与凸轮接触，且OAB成一直线。求：在图示位置时，杆AB的速度。 解：1、动点：AB杆上A动系：凸轮牵连运动：定轴运动（轴O）相对运动：圆周运动（半径R）2、绝对运动：直线运动（AB）3、大小方向√　√　√ 例8-6　圆盘半径为R，以角速度ω1绕水平轴CD转动，支承CD的框架又以角速度ω2绕铅直的AB轴转动，如图所示。圆盘垂直于CD，圆心在CD与AB的交点O处。求：当连线OM在水平位置时，圆盘边缘上的点M的绝对速度。 解：1、动点：M点动系：框架BACD牵连运动：定轴转动（AB轴)相对运动：圆周运动（圆心O点）2、绝对运动：未知3、大小？方向？√　√ 在图a和b所示的两种机构中，己知O1O2=a=200mm，ω=3rad/s。求图示位置时杆O2A的角速度。 图示两盘匀速转动的角速度分别为ω1=1rad/s、ω2=2rad/s，两盘半径均为R=50mm，两盘转轴距离L=250mm。图示瞬时，两盘位于同一平面内。求此时盘2上的点A相对于盘1的速度。 图示铰接四边形机构中，O1A=O2B=100mm，又O1O2=AB，杆O1A以等角速度ω=2rad/s绕O1轴转动。杆AB上有一套筒C，此筒与杆CD相铰接。机构的各部件都在同一铅直面内。求当φ=60º时，杆CD的速度。 r=R+r’=R+x’i’+y’j’§８-３点的加速度合成定理 1.动系作平移 例8-7平面曲柄推杆机构如图所示，推杆BC可沿导轨上下移动，曲柄OA=l，绕轴O转动的角速度ω为常数，求当OA与铅垂线成夹角φ时，推杆的加速度。 解:1.动点=滑块A，动系=推杆BC2。分析三种运动绝对运动:圆周运动相对运动:直线运动牵连运动:平移aa=ae+ar3。加速度合成公式大小2l??方向 2.动系作定轴转动 牵连点M1 —科氏加速度（Coriolisacceleration） 例8-8　刨床的急回机构如图所示。曲柄OA的一端A与滑块用铰链连接。当曲柄OA以匀角速度ω绕固定轴O转动时，滑块在摇杆O1B上滑动，并带动杆O1B绕定轴O1摆动。设曲柄长为OA=r，两轴间距离OO1=l。求:摇杆O1B在如图所示位置时的角加速度。 解：1、动点：滑块A动系：O1B杆绝对运动：圆周运动相对运动：直线运动（沿O1B）牵连运动：定轴转动（绕O1轴）2、速度大小方向√　√　√ 3、加速度√√√√√大小方向沿轴投影 例8-9　如图所示平面机构中，曲柄OA=r，以匀角速度ωO转动。套筒A沿BC杆滑动。已知：BC=DE，且BD=CE=l。求：图示位置时，杆BD的角速度和角加速度。 解：1、动点：滑块A动系：BC杆绝对运动：圆周运动（O点）相对运动：直线运动（BC）牵连运动：平移2、速度√√√ 3、加速度√√√√沿y轴投影 求：该瞬时AB的速度及加速度。例8-10　如图所示凸轮机构中，凸轮以匀角速度ω绕水平O轴转动，带动直杆AB沿铅直线上、下运动，且O，A，B共线。凸轮上与点A接触的为，图示瞬时凸轮上点曲率半径为ρA，点的法线与OA夹角为θ，OA=l。 绝对运动：直线运动（AB）相对运动：曲线运动（凸轮外边缘）牵连运动：定轴转动（O轴）解：1、动点（AB杆上A点）动系：凸轮O2、速度√√√3、加速度√√√√√沿轴投影 例8-11圆盘半径R=50mm，以匀角速度ω1绕水平轴CD转动。同时框架和CD轴一起以匀角速度ω2绕通过圆盘中心O的铅直轴AB转动，如图所示。如ω1=5rad/s,ω2=3rad/s。求：圆盘上1和2两点的绝对加速度。 解：1、动点：圆盘上点1（或2）动系：框架CAD绝对运动：未知相对运动：圆周运动（O点）牵连运动：定轴转动（AB轴）2、速度（略）3、加速度×√√　√点1的牵连加速度与相对加速度在同一直线上，于是得 点２的牵连加速度科氏加速度大小为相对加速度大小为与铅垂方向夹角各方向如图，于是得