理论力学课件chap7幻灯片课件.ppt

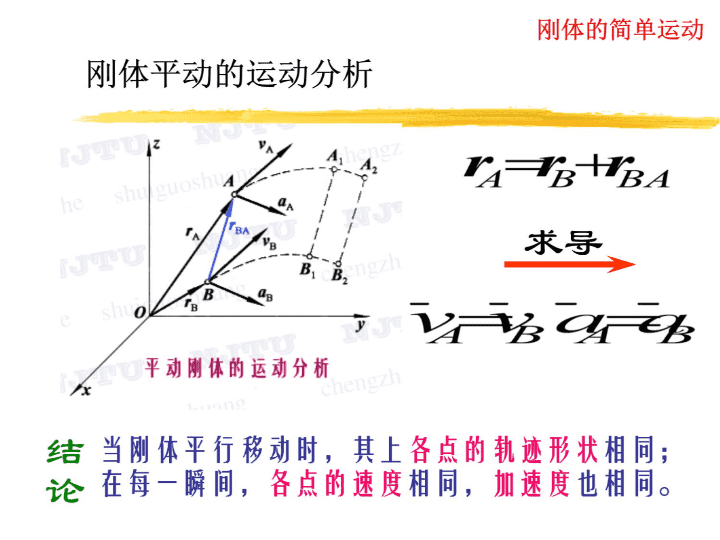
刚体的简单运动刚体的平动刚体绕定轴的转动转动刚体内各点的速度和加速度以矢量表示角速度和角加速度以矢积表示点的速度和加速度 刚体的简单运动1.平（行移）动Translation任一直线总是平行于自己的初始位置 例1荡木用两条等长的钢索平行吊起，钢索的摆动规律为。试求当t=0和t=2s时，荡木中点M的速度和加速度。0+ 解：vAaAtaAn刚体的简单运动 注意:刚体运动:刚体上点的运动：各点的运动轨迹均为圆平面曲线平移，并不作转动刚体的简单运动vAaAtaAn 2.定轴转动刚体的运动刚体的简单运动 2.定轴转动刚体的运动刚体在运动时，其上有两点始终保持不动刚体的简单运动 定轴转动刚体的运动定轴转动刚体的运动方程刚体的瞬时角速度刚体的瞬时角加速度逆时针为正逆时针为正刚体的简单运动 例2如图所示，曲柄CB以匀角速度0绕C轴转动，其转动方程为＝0t，通过滑块B带动摇杆OA绕O转动，设OC＝h，CB＝r，求摇杆的转动方程。解：又＝0t摇杆的转动方程为： 定轴转动刚体上各点的运动运动方程：速度：刚体的简单运动 定轴转动刚体上各点的运动加速度：刚体的简单运动 定轴转动刚体上各点的运动加速度方程：刚体的简单运动 刚体的简单运动 刚体的简单运动例3如图所示，摇杆机构的滑杆AB以匀速u向上运动，试建立摇杆OC上点C的运动方程，并求此点在的速度大小。假定初始瞬时＝0，摇杆长OC＝a，距离OD＝l。 解：直角坐标法：动点C的运动方程：弧坐标点C的运动方程：当例3如图所示，摇杆机构的滑杆AB以匀速u向上运动，试建立摇杆OC上点C的运动方程，并求此点在的速度大小。假定初始瞬时＝0，摇杆长OC＝a，距离OD＝l。 例4电影胶片以恒速v从卷盘中拉出，从而带动卷盘和尚未拉出的胶片一起作绕固定轴的转动。若胶片的厚度为δ，正滚动着的胶片的半径为r，试求卷盘的角加速度ε，设s与r相比很大。解：设卷盘中胶片初始半径为r0。当卷盘转了φ角时，半径r的表达式vs 例5纸盘由厚度为a的纸条卷成,纸盘的中心不动,以等速v拉纸条。求纸盘的角加速度。解：设纸盘初始半径为R，则在任意时刻t时纸盘减少的面积为：在任意时刻t时的速度与角速度之间都存在：对上两式求导：将(1)式代入(2)式： 定轴转动刚体及刚体上各点运动的矢量表示1.刚体运动的角速度矢量与角加速度矢量：滑移矢量刚体的简单运动 2.刚体上一点的速度：刚体的简单运动3.刚体上一点的加速度坐标原点过转轴 刚体上固定矢量对时间的变化率：应用：对于固结于定轴转动刚体上的动参考系，若其单位矢为i、j、k，则单位矢对时间的变化率？刚体的简单运动-平动和定轴转动 单位矢对时间的变化率：（泊松公式）刚体的简单运动 齿轮传动特征一：接触点速度相同；特征二：接触点切向加速度相同；齿数Z与半径R成正比特征三：传动比i主动轮和从动轮角速度之比刚体的简单运动 图示机构中齿轮1紧固在杆AC上,AB=O1O2,齿轮1和半径为r2的齿轮2啮合,齿轮2可绕O2轴转动且和曲柄O2B没有联系。设，.试确定时,轮2的角速度和角加速度。 图示机构中齿轮1紧固在杆AC上,AB=O1O2,齿轮1和半径为r2的齿轮2啮合,齿轮2可绕O2轴转动且和曲柄O2B没有联系。设，.试确定时,轮2的角速度和角加速度。解：由于ACB作平动：D 例6带式输送机如图。已知主动轮Ⅰ的转速n1=1200r/min，齿数z1=24，齿轮Ⅲ和Ⅳ用链条来传动，齿数各为z3=15和z4=45，轮Ⅴ的直径D=460mm，如希望输送带的速度约为2.4m/s，试求轮Ⅱ应有的齿数n2。刚体的简单运动 解：由图示传动关系有：例6带式输送机如图。已知主动轮Ⅰ的转速n1=1200r/min，齿数z1=24，齿轮Ⅲ和Ⅳ用链条来传动，齿数各为z3=15和z4=45，轮Ⅴ的直径D=460mm，如希望输送带的速度约为2.4m/s，试求轮Ⅱ应有的齿数Z2。 本章习题4–5678习题要求1）要抄题，画原图；2）运动状态参量求得后要在图上画明；3）参照系要画清楚；刚体的简单运动 圆盘以恒定的角速度绕垂直于盘面的中心轴转动,该轴y-z在面内,倾斜角,点A的矢径在图示瞬时为.求点A的速度和加速度的矢量表达式，并用和检验所得结果是否正确。解：将矢量在y-z面内分解 半径R=100mm的圆盘绕其圆心转动,图示瞬时A点的速度为vA=200jmm/s,点B的切向加速度aBt=150imm/s2。试求角速度和角加速,并进一步写出点C的加速度的矢量表达式。解：zkB 课堂讨论刚体的简单运动 课堂讨论下列说法是否正确：1平动刚体上的点的运动轨迹不可能是空间曲线。×平动只要求刚体上任一直线在空间的方位不变，点的运动轨迹有可能是空间曲线。2定轴转动刚体的固定转轴不能在刚体的外轮廓之外。×转轴在刚体外时，刚体也可作定轴转动。如汽车车身在十字路口转弯时，就有可能绕岗亭中心线作定轴转动。 课堂讨论3定轴转动刚体的角加速度为正值时，刚体一定越转越快。×刚体定轴转动是否越转越快，主要看角加速度和角速度的转向是否相同，只有转向一致时才会越转越快。