理论力学课件第一篇静力学第四章 空间任意力系x.ppt

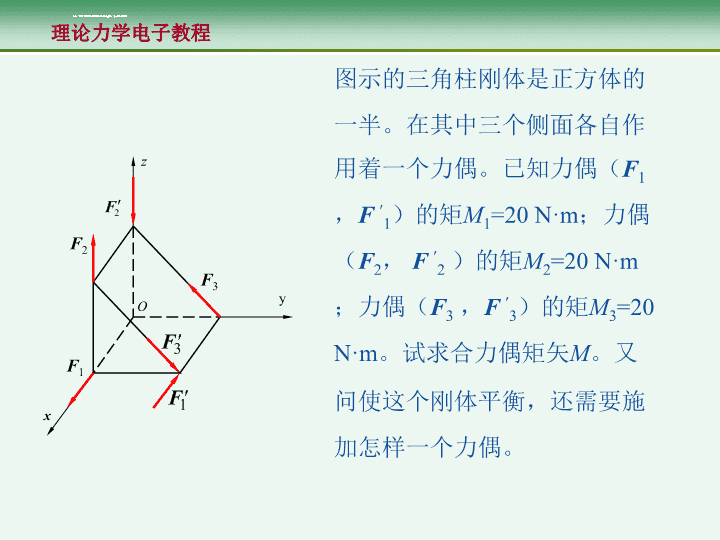
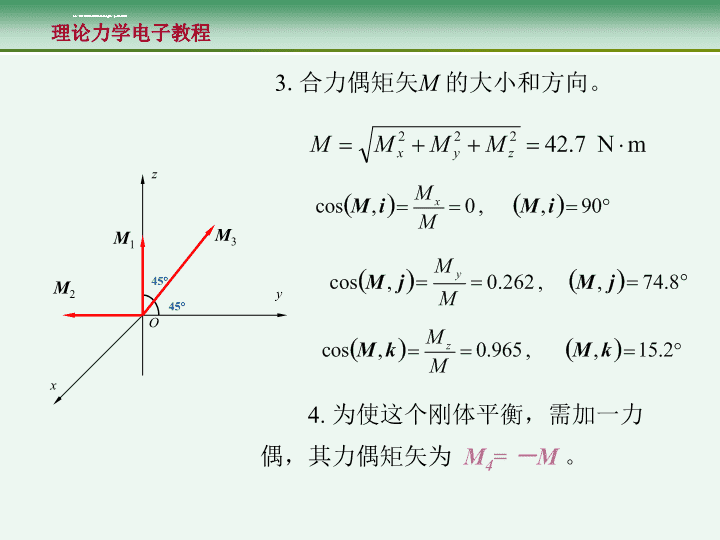
xzyOF1F2F3图示的三角柱刚体是正方体的一半。在其中三个侧面各自作用着一个力偶。已知力偶（F1，F1）的矩M1=20N·m；力偶（F2，F2）的矩M2=20N·m；力偶（F3，F3）的矩M3=20N·m。试求合力偶矩矢M。又问使这个刚体平衡，还需要施加怎样一个力偶。 1.画出各力偶矩矢。2.合力偶矩矢M的投影。解：xzy45°OM145°M2M3 3.合力偶矩矢M的大小和方向。4.为使这个刚体平衡，需加一力偶，其力偶矩矢为M4=－M。xzy45°OM145°M2M3 CA5mBDEG桅杆式起重机可简化为如图所示结构。AC为立柱，BC，CD和CE均为钢索，AB为起重杆。A端可简化为球铰链约束。设B点滑轮上起吊重物的重量P=20kN，AD=AE=6m，其余尺寸如图。起重杆所在平面ABC与对称面ACG重合。不计立柱和起重杆的自重，求起重杆AB、立柱AC和钢索CD，CE所受的力。 CA5mBDEG1.先取滑轮B为研究对象。注意，起重杆AB为桁架构件，两端铰接，不计自重，它是一个二力构件，把滑轮B简化为一点，它的受力图如图所示。xyBPFABFBC解：这是一平面汇交力系，列平衡方程解得 2.再选取C点为研究对象，它的受力图如图所示。此力系在Axy平面上投影为一平面汇交力系，其中：先列出对Az轴的投影方程这是一空间汇交力系，作直角坐标系Axy，把力系中各力投影到Axy平面和Az轴上。xzAyCFACFCEFCD 列平衡方程由此解得所求结果如下：xzAyCFACFCEFCD 第四章空间任意力系第一节空间任意力系的简化第三节一般平行分布力的简化第四节重心、质心和形心第二节空间任意力系的平衡条件平衡方程 第一节空间任意力系的简化第一节空间任意力系的简化 第一节空间任意力系的简化一、空间任意力系向一点简化设有空间任意力系F1、F2、…、Fn，各力分别作用于A1、A2、……、An各点。任取一点Ｏ作简化中心，将各力平行移至Ｏ点，并各附加一力偶，得到一个汇交力系和一个附加力偶系。 图4-1空间任意力系向O点简化第一节空间任意力系的简化各附加力偶矩应作为矢量，分别垂直于相应的力与Ｏ点所决定的平面，并分别等于相应的力对于Ｏ点的矩。 汇交力系Ｆ1′、Ｆ2′、…、Ｆn′可合成为一个力ＦR，等于各力的矢量和，即ＦR=Ｆ1′+Ｆ2′+…+Ｆn′，亦即：(4-1)附加力偶系可合成为一个力偶，力偶矩ＭO等于各附加力偶矩的矢量和，即MO=M１+M2+……+Mn，亦即等于原力系中各力对于简化中心的矩的矢量和(4-2)矢量称为原力系的主矢量，矢量称为原力系对于简化中心Ｏ的主矩。第一节空间任意力系的简化 可知，空间力系向一点（简化中心）简化的结果一般是一个力和一个力偶，这个力作用于简化中心，等于原力系中所有各力的矢量和，亦即等于原力系的主矢量；这个力偶的矩等于原力系中所有各力对于简化中心的矩的矢量和，亦即等于原力系对于简化中心的主矩。如果选取不同的简化中心，主矢量并不改变，所以，一个力系的主矢量是一常量，与简化中心的位置无关。但是，力系中各力对于不同的简化中心的力矩是不同的，因而它们的矢量和一般说来也不相等。所以，主矩一般将随简化中心位置不同而改变。第一节空间任意力系的简化 对于不同的两个简化中心及来说，力系对于它们的主矩之间存在如下的关系：(4-3)由此可知，当简化中心沿主矢量　　的作用线移动时，主矩将保持不变。为了计算主矢量和主矩，可过简化中心取直角坐标系Oxyz。由(4-4)第一节空间任意力系的简化 得到：而Ｆ的大小及方向余弦为：(4-6)（4-5）第一节空间任意力系的简化 相似地，主矩Ｍo在坐标轴上的投影Ｍx、Ｍy、Ｍz，则分别等于各力对Ｏ点的矩在对应轴上的投影之和，亦即等于各力对于对应轴的矩之和，即：上式还可写成：（4-7）（4-8）第一节空间任意力系的简化 已知主矩Ｍo的投影，则可求得Ｍo的大小及方向余弦为：(4-9)第一节空间任意力系的简化 二、空间平行力系取z轴平行于各力作用线，则有FRx≡0，FRy≡0,Mz≡0，得：(4-10)可见：FR平行于z轴，而MO垂直于z轴，所以FR与ＭO互相垂直。第一节空间任意力系的简化 三、空间任意力系简化结果讨论若FR＝０，MO≠０，则原力系简化为一个合力偶，合力偶矩等于原力系对于简化中心的主矩。在这种情况下，主矩（即力偶矩）将不因简化中心位置的不同而改变。1、空间任意力系简化为一合力偶第一节空间任意力系的简化 若FR≠０，MO＝０，则原力系简化为一个合力，合力的作用线通过简化中心O点，其大小和方向等于原力系的主矢量。第一节空间任意力系的简化若FR≠０，MO≠０，但MO⊥FR，这表明MO所代表的力偶与FR在同一平面内，于是，可以继续合成为一个合力FR′,如图4-2所示。2、空间任意力系简化为一合力 图4-2第一节空间任意力系的简化合力FR′的大小和方向等于原力系的主矢量，其作用线至简化中心的距离为：d=|Mo|/FR若空间任意力系可简化成为一个合力，则合力对任一点（或轴）的矩等于原力系各力对同一点（或轴）的矩的矢量和（或代数和）。空间任意力系的合力矩定理 空间任意力系的合力矩定理数学表达式为：（4-12）（4-13）借助于图（4-2）可证明合力矩定理（略）第一节空间任意力系的简化对于空间平行力系，当FR和MO都不等于零时，MO总是垂直于FR，所以必能简化成为一个合力，合力矩定理也必定成立，且由合力矩定理可以确定合力作用线位置。 若FR≠０，MO≠０，且MO与FR不相垂直，如图（4-3a），则可用下述方法进一步简化。图4-3力螺旋第一节空间任意力系的简化3、空间任意力系简化为一合力螺旋 这样的一个力和一个力偶称为力螺旋。直线O′P称为原力系的中心轴；如MR与FR同方向，则称为右手螺旋；如MR与FR方向相反，则称为左手螺旋。力螺旋是空间力系简化的最简单形式。而且，对于确定的空间力系，组成力螺旋的力和力偶矩是确定的，力螺旋的中心轴的位置也是确定的，MR是力系的最小主矩。第一节空间任意力系的简化 第二节空间任意力系的平衡条件平衡方程第二节空间任意力系的平衡条件平衡方程 第二节空间任意力系的平衡条件平衡方程如果空间任意力系的主矢量及对于任意简化中心的主矩同时等于零，则该力系为平衡力系。反之，如空间任意力系成平衡，其主矢量与对于任一简化中心的主矩必分别等于零。空间任意力系成平衡的必要与充分条件是力系的主矢量与力系对于任一点的主矩都等于零。FR＝０，MO＝０（4-15）即: 过O点取直角坐标系Oxyz，上述条件可用代数方程表示为：（4-16）式（4-16）的六个方程就是空间任意力系的平衡方程。它们表示：力系中所有的力在三个直角坐标轴中的每一轴上的投影的代数和等于零，所有的力对于每一轴的矩的代数和等于零。第二节空间任意力系的平衡条件平衡方程 对空间平行力系，令z轴平行于各力，则∑Fix≡０，∑Fiy≡０，∑Miz≡０。空间平行力系的平衡方程成为：Fiz=0，Mix＝０，Miy＝０（4-17）注意：方程（4-16）虽然是由直角坐标系导出的，但在解答具体问题时，不一定使三个投影轴或矩轴垂直，也没有必要使矩轴和投影轴重合而可以分别选取适宜轴线为投影轴或矩轴，使每一平衡方程中包含的未知量最少，以简化计算。第二节空间任意力系的平衡条件平衡方程 式(4-16)称为平衡方程的基本形式有时为了方便，也可减少平衡方程中的投影方程，而增加力矩方程。如取二个投影方程和四个力矩方程(四力矩形式)，或取一个投影方程和五个力矩方程(五力矩形式)，或全部取六个力矩方程(六力矩形式)，但不管采用何种平衡方程的形式，它最多只能有六个独立的平衡方程。但要注意，不同平衡方程形式中投影轴与矩轴需满足一定的条件，才能保证方程是相互独立的。第二节空间任意力系的平衡条件平衡方程 悬臂刚架ABC上作用有分布荷载q=1kN/m,P=3kN,Q=4kN及力偶矩2kNm,刚架各部分尺寸如图示.求固定端A处的约束反力及力偶矩. 【解】作受力图,建坐标系求解得: 若负值说明与设定方向相反。 三轮卡车自重(包括车轮重)Fw=8kN，载重Fp=10kN，作用点位置如图4-4所示，求静止时地面作用于三个轮子的反力。图中长度单位为m。图4-４例4-1附图例4-1第二节空间任意力系的平衡条件平衡方程 解：作三轮卡车的受力图，各力组成一平衡的空间平行力系。取坐标轴如图，写出平衡方程求解各未知量。解得：例4-1第二节空间任意力系的平衡条件平衡方程 解得：解得：例4-1第二节空间任意力系的平衡条件平衡方程 重Fw=100N的均质矩形板ABCD,在A点用球铰，B点用普通铰链，并用绳DE支承于水平位置（图4-5）。力FP作用在过C点的铅直面内。设力FP的大小为200N，a=1m，b=0.4m，α=45o，求A、B两处的约束力及绳DE的拉力。图4-5例4-2附图例4-2第二节空间任意力系的平衡条件平衡方程 解:考虑矩形板的平衡。球铰和铰链的约束力，用它们的分量表示如图，并设绳子的拉力为FT。取坐标系如图所示。按以下次序列平衡方程(1)(2)(3)例4-2第二节空间任意力系的平衡条件平衡方程 (4)(5)(6)解之得：例4-2第二节空间任意力系的平衡条件平衡方程 某厂房支承屋架和吊车梁的柱子如图4-6所示，下端固定。柱顶承受屋架传来的力FP1，牛腿上承受吊车梁传来的铅直力FP2及水平制动力FT。例4-3第二节空间任意力系的平衡条件平衡方程图4-6例4-3附图 图4-6例4-3附图已知：e1＝0.1m，e2＝0.34m，h＝6m，FP1＝120kN，FP2＝300kN，制动力FT平行于x轴，FT＝25kN，柱所受重力FQ可认为沿z轴作用，且FQ＝40kN。试求基础对柱作用的约束力及力偶矩。例4-3第二节空间任意力系的平衡条件平衡方程 图4-6例4-3附图解:柱子下端的约束力和约束力偶如图示。事实上固定端的约束力是作用在柱端表面的一个分布力，向Ｏ点简化后可得到一个力和一个力偶，计算时用其分量表示。例4-3第二节空间任意力系的平衡条件平衡方程 按以下次序列六个平衡方程例4-3第二节空间任意力系的平衡条件平衡方程 将已知值代入，解得：Fox＝25kN，Foy＝0，Foz＝460kN，Mox＝90kN·m，Moy＝150kN·m，Moz＝－8.5kN·m。例4-3第二节空间任意力系的平衡条件平衡方程 第三节一般平行分布力的简化第三节一般平行分布力的简化 第三节一般平行分布力的简化一、沿平面曲线分布的平行力沿狭长面积分布的平行力可以简化为沿平面曲线分布的平行力。设力沿平面曲线AB分布，则荷载图成为一曲面。取直角坐标系的z轴平行于分布力，曲线AB位于xy平面内。 令坐标为x、y处的荷载集度为q，则在该处微小长度Δs上的力的大小为ΔF＝qΔs，亦即等于Δs上荷载图的面积ΔA。于是，线段AB上所受的力的合力大小等于:F＝∑ΔF＝∑qΔs＝∑ΔA＝线段AB上荷载图的面积。第三节一般平行分布力的简化 合力F的作用线位置可用合力矩定理求得。分别对y轴及x轴求矩有:xcF＝∑xqΔs＝∑xΔA-ycF＝-∑yqΔs＝-∑yΔA由此得：这就是荷载图形心的x坐标和y坐标。沿平面曲线分布的平行分布力的合力的大小等于荷载图的面积，合力作用线通过荷载图面积的形心。(4-18)第三节一般平行分布力的简化 二、平行分布于平面上的力如图4-8为面积A上的荷载图，取直角坐标系的中z轴平行于分布力，荷载作用面为xy面。在面积A内坐标为（x，y）处取微小面积ΔA，若该处荷载集度为p，则微小面积ΔA上所受的力的大小为ΔF＝pΔA，亦即等于ΔA上荷载图的体积ΔV。图4-8面积A上的分布力第三节一般平行分布力的简化 面积A上所受的力的合力大小为：=面积Ａ上荷载图的体积。第三节一般平行分布力的简化合力作用线的位置仍用合力矩定理求出，可得可见，平行分布的面力的合力的大小等于荷载图的体积，合力通过荷载图体积的形心。 水平半圆形（半径Ｒ）梁上受铅直分布荷载，其集度按q=qosinθ变化，如图(4-9)所示。求分布荷载的合力的大小及作用线位置。图4-9例4-4附图例4-4第三节一般平行分布力的简化 解：首先求合力F的大小。在θ处，长ds=Rdθ的梁上所受的力dF=qRdθ=Rqosinθdθ，所以整个梁上所受荷载的合力的大小为：再求F的作用线位置。设作用线与xy平面的交点为C。由对称性，点C必位于y轴上，故xC=0，只需求yC。例4-4第三节一般平行分布力的简化 由合力矩定理，可得：于是得到：例4-4第三节一般平行分布力的简化 第四节重心、质心和形心第四节重心、质心和形心 第四节重心、质心和形心重心的位置对于物体的平衡和运动，都有很大关系。在工程上，设计挡土墙、重力坝等建筑物时，重心位置直接关系到建筑物的抗倾覆稳定性及其内部的受力状态。机械的转动部分，有的（如偏心轮）应使其重心离开转动轴一定的距离，以便利用由于偏心而产生的效果；有的（特别是高速转动者）却必须使其重心尽可能不偏离转动轴，以避免产生不良影响。所以，如何确定物体重心的位置，在实践上有着重要意义。 一、基本公式设物体任一微小部分Mi所受的重力为△FPi，所有各力△FPi（i=1,2,…,n）的合力FP就是整个物体所受的重力。不论物体在空中取什么样的位置，合力FP的作用线必通过某一确定点C，这一点C就称为物体的重心。第四节重心、质心和形心各部分的ΔFPi可以看作平行力，所以，合力的大小FP＝∑ΔFPi，而物体重心位置则可利用合力矩定理求得。 由于工程上的物体都远较地球为小，离地心又很远，所以各部分的ΔFPi可以看作平行力而足够精确。这样，合力FP的大小（即整个物体的重量）FP＝∑ΔFPi，而物体重心位置则可利用合力矩定理求得。为此，使物体固定于坐标系Oxyz内。令Mi及Ｃ相对于Ｏ点的矢径为ri及rC。第四节重心、质心和形心 由合力矩定理有：沿重力的方向取单位矢量p0，则：可得：第四节重心、质心和形心或无论p0的方向如何，上式恒成立，即得 或：(4-20)将上式两边投影到x、y、z轴上，即得求物体重心公式：（4-21）第四节重心、质心和形心 如微小部分Mi的质量为Δmi，物体的质量为m，重力加速度为g，则ΔFPi=Δmig，FP=mig。由求重心的公式（4-20）可得:（4-22）由式（4-22）所确定的C点称为物体的质心，可见，在地面附近物体的重心与质心是重合的。相应地，式(4-21)成为：（4-23）第四节重心、质心和形心 如果物体是均质的，即质量密度ρ是常数，则每单位体积的重力γ也为常数，命Mi的体积为ΔVi，整个物体的体积为Ｖ＝∑ΔVi，则ΔFPi=γΔVi，FP=γＶ，而代入式（4-21）或式（4-23），就得到：（4-24）第四节重心、质心和形心 式(4-24)表明，对于均质物体，其重心和质心的位置完全决定于物体的几何形状。由式(4-24)所确定的点Ｃ便称为几何形体的形心。对于曲面或曲线，只须在公式（4-24）中分别将ΔVi改为ΔAi(面积)或ΔLi(长度)，V改为A或L，即可得相应的重心坐标公式。对于平面图形或平面曲线，如取所在的平面为xy面，则显然zc＝０，而xc及yc可由公式（4-24）中的前两式求得。第四节重心、质心和形心 在公式（2-29）中，如令ΔV趋近于零而取和式的极限，可得到计算形心坐标的积分公式为：(4-25)由形心计算公式可见，凡具有对称面、对称轴或对称中心的均质物体（或几何形体)，其重心(或形心）必定在对称面、对称轴或对称中心上。第四节重心、质心和形心书中表4-1给出了一些常见简单形体的形心坐标公式。 二、组合形体形状较复杂的形体，往往可以看作几个简单形体的组合。设已知各简单形体的重量FPi（或体积Vi、或面积Ai、或长度Li）及其重心（或形心）的位置，只要用FPi（或Vi、Ai、Li）代换以上各公式中的ΔFPi（或ΔVi、ΔAi、ΔLi），用各简单形体的重心（或形心）的坐标xCi、yCi、zCi代替xi、yi、zi，就可求得整个形体的重心（或形心）的位置。对于形状复杂又不能分成若干个简单形体的物体，就只能用近似方法或用实验方法求其重心（或形心）。第四节重心、质心和形心 求图示圆弧AB的形心坐标。解：取坐标如图。由于图形对称于x轴，因而yc＝０。为了求xc，取微小弧段ds＝rdθ，其坐标为x＝rcosθ，于是得到：例4-5第四节重心、质心和形心 在均质圆板内挖去一扇形面积。已知R＝300mm，r1＝250mm，r2＝100mm，求板的重心位置。解：取坐标轴如图。因x轴为板的对称轴，重心必在对称轴上，即yc＝０，所以，只须求重心的坐标xc。例4-6第四节重心、质心和形心 将板看成：在半径为R的圆面积上挖去一半径为r1而圆心角为2α＝60°的扇形面积，再加上一半径为r2而圆心角为2α＝60°的扇形面积。各部分面积分别用A1、A2、A3表示。因A2系挖去的面积，应取为负值（故这种方法称为负面积法）。各部分面积及其重心坐标计算如下：例4-6第四节重心、质心和形心 例4-6第四节重心、质心和形心代入形心计算公式，可得：