理论力学课件

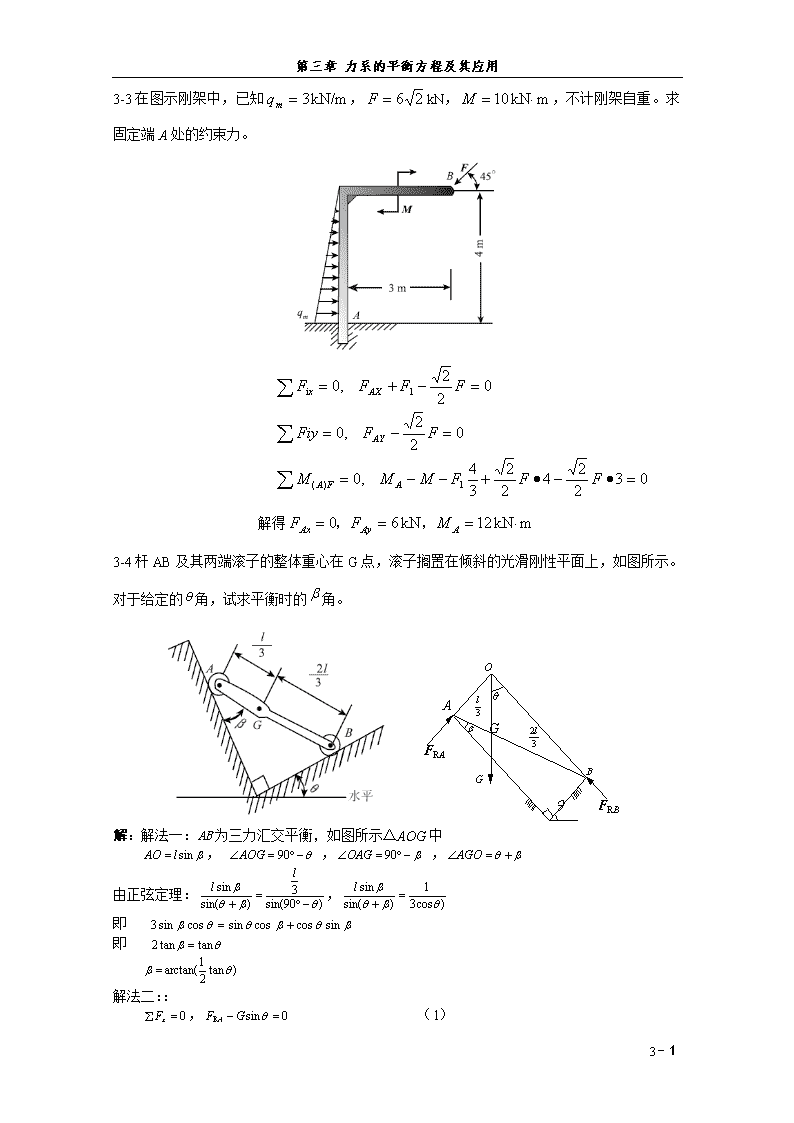
第三章力系的平衡方程及其应用3-3在图示刚架中，已知，kN，，不计刚架自重。求固定端A处的约束力。解得3-4杆AB及其两端滚子的整体重心在G点，滚子搁置在倾斜的光滑刚性平面上，如图所示。对于给定的角，试求平衡时的角。解：解法一：AB为三力汇交平衡，如图所示ΔAOG中，，，由正弦定理：，即即解法二：：，（1）3－１５ 第三章力系的平衡方程及其应用，（2），（3）解（1）、（2）、（3）联立，得3-5由AC和CD构成的组合梁通过铰链C连接。支承和受力如图所示。已知均布载荷强度，力偶矩，不计梁重。解：取CD段为研究对象，受力如图所示。，；取图整体为研究对象，受力如图所示。，；，；，解得3-6如图所示，组合梁由AC和DC两段铰接构成，起重机放在梁上。已知起重机重P1=50kN，重心在铅直线EC上，起重载荷P2=10kN。如不计梁重，求支座A、B和D三处的约束反力。3－１５ 第三章力系的平衡方程及其应用解：（1）取起重机为研究对象，受力如图。，，（2）取CD为研究对象，受力如图，，（3）整体作研究对象，受力图（c），，，，3-7构架由杆AB，AC和DF铰接而成，如图所示。在DEF杆上作用一矩为M3－１５ 第三章力系的平衡方程及其应用的力偶。不计各杆的重量，求AB杆上铰链A，D和B所受的力。解对整体（图（a）），有解得再研究DEF杆（图（b）），有3－１５ 第三章力系的平衡方程及其应用解得3-8图示构架中，物体P重1200N，由细绳跨过滑轮E而水平系于墙上，尺寸如图。不计杆和滑轮的重量，求支承A和B处的约束力，以及杆BC的内力FBC。解：（1）整体为研究对象，受力图（a），，，，，（2）研究对象CDE（BC为二力杆），受力图（b），（压力）3-9图示结构中，A处为固定端约束，C处为光滑接触，D处为铰链连接。已知，，，，，不计各构件自重，求固定端A处与铰链D处的约束力。3－１５ 第三章力系的平衡方程及其应用解先研究DCE杆，如图（a），由解得再研究ABC杆，如图（b），由解得3-10图示结构由直角弯杆DAB与直杆BC、CD铰接而成，并在A处与B处用固定铰支座和可动铰支座固定。杆DC受均布载荷q的作用，杆BC受矩为的力偶作用。不计各构件的自重。求铰链D受的力。3－１５ 第三章力系的平衡方程及其应用解先研究BC杆，受力如图（b），由得CD杆受力如图（a），由解得3-11图示构架，由直杆BC，CD及直角弯杆AB组成，各杆自重不计，载荷分布及尺寸如图。在销钉B上作用载荷P。已知q、a、M、且。求固定端A的约束力及销钉B对BC杆、AB杆的作用力。3－１５ 第三章力系的平衡方程及其应用解先研究CD杆如图（b），由解得研究BC杆（包括销钉B），受力如图（d），由解得A处约束反力研究销钉B如图（e），图中、是BC杆对销钉B的作用力解得3－12无重曲杆ABCD有两个直角，且平面ABC与平面BCD垂直。杆的D端为球铰支座，A端为轴承约束，如图所示。在曲杆的AB、BC和CD上作用三个力偶，力偶所在平面分别垂直于AB、BC和CD三线段。已知力偶矩M2和M3，求使曲杆处于平衡的力偶矩M1和处的约束力。3－１５ 第三章力系的平衡方程及其应用解：如图所示：，，，，，，3－13在图示转轴中，已知：Q=4KN，r=0.5m，轮C与水平轴AB垂直，自重均不计。试求平衡时力偶矩M的大小及轴承A、B的约束反力。解：3－１５ 第三章力系的平衡方程及其应用3－14匀质杆AB重Q长L，AB两端分别支于光滑的墙面及水平地板上，位置如图所示，并以二水平索AC及BD维持其平衡。试求（1）墙及地板的反力；（2）两索的拉力。解：3－14平面悬臂桁架所受的载荷如图所示。求杆1，2和3的内力。3－１５ 第三章力系的平衡方程及其应用解用截面法取分离如图（b），由解得再研究节点B，受力如图（c）由得3－15平面桁架的支座和载荷如图所示。ABC为等边三角形，E，F为两腰中点，又AD=DB。求杆CD的内力。ED为零杆，取BDF研究，FCD=-0.866F3－16桁架受力如图所示，已知，。试求桁架4，5，7，10各杆的内力。3－１５ 第三章力系的平衡方程及其应用解先研究整体如图（a），由解得再用截面法取分离体如图（b）,由解得最后研究节点G，如图（c），由3－１５ 第三章力系的平衡方程及其应用解得3－17平面桁架的支座和载荷如图所示，求杆1，2和3的内力。解用截面法，取CDF部分，受力如图（b），由解得接着研究节点C，受力如图(c),有得（压）3－18均质圆柱重P、半径为r，搁在不计自重的水平杆和固定斜面之间。杆端A为光滑铰链，D端受一铅垂向上的力，圆柱上作用一力偶。如图所示。已知，圆柱与杆和斜面间的静滑动摩擦系数皆为fS=0.3，不计滚动摩阻，当时，AB=BD。求此时能保持系统静止的力偶矩M的最小值。3－１５ 第三章力系的平衡方程及其应用解先研究ABD杆，受力如图（a），由解得再研究圆柱，设它平衡，受力如图（b），则有设E点先达到临界滑动状态，则有联立解得(假设成立)若B点先达到临界滑动状态，则联立式（1）（2）（3）（5），解得(假设不成立)这说明B处不可能先于E处到达临界状态，故3－19如图所示，A块重500N，轮轴B重1000N，A块与轮轴的轴以水平绳连接。在轮轴外绕以细绳，此绳跨过一光滑的滑轮D，在绳的端点系一重物C。如A块与平面间的摩擦系数为0.5，轮轴与平面间的摩擦系数为0.2，不计滚动摩阻，试求使系统平衡时物体C的重量P的最大值。3－１５ 第三章力系的平衡方程及其应用解设该系统平衡，对轮轴，有对物A，有先设轮轴即将滚动，但不打滑，使物块A即将滑动，则解得即轮轴在即将滚动时确实不会打滑。再设轮轴即将打滑，物块A仍不动，对轮轴有联立（1）（2）（4）（5）（7）各式，可解得(假设不成立)即此时物块A已经不能平衡。因此，全系统平衡时物体C的重量P的最大值3－１５