应力状态(II)--水电、土木

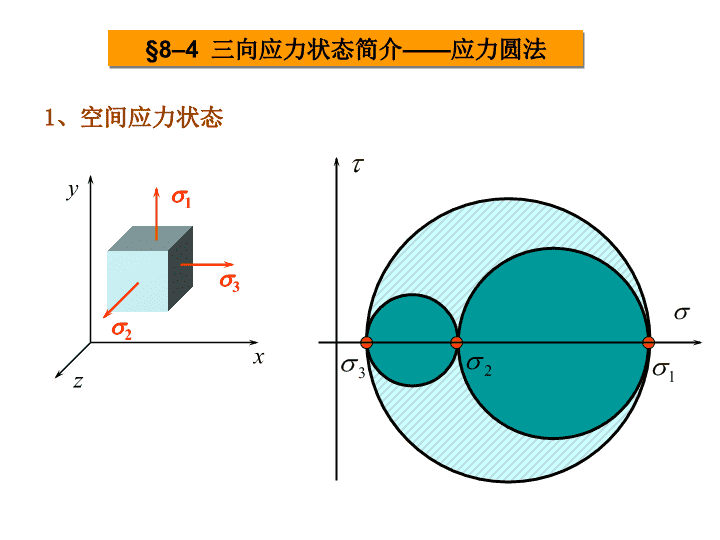
第八章应力状态分析与强度理论 §8–4三向应力状态简介——应力圆法s3s1xyzs21、空间应力状态 s3s1xyzs22、三向应力状态分析tmax弹性理论证明，图a单元体内任意截面上的应力都对应着图b的应力圆上或阴影区内的一点。整个单元体内的最大剪应力为： §8–5复杂应力状态下的应力--应变关系——（广义胡克定律）一、单向应力状态的应力--应变关系二、纯剪的应力--应变关系xyzsxxyzxy 三、三向应力状态下的应力---应变关系xyzszsysx依叠加原理,得: xyztxy 一般单元体情况下单元体分解,得:xyzszsytxysxxyzszsysxxyztxy 依叠加原理,得:xyzszsysxxyztxy 主应变：s1s3s2单元体上沿主应力方向的应变称为主应变。主应力---主应变关系结论：过一点的各个方向的应变中，沿最大主应力方向的主应变最大。沿最小主应力方向的主应变最小。s1s3 四、平面应力状态下的应力---应变关系:xyzsztxysxsyxyztxysxsy 五、体积应变体积应变：体积应变与应力分量间的关系:s1s3s2a1a2a3 一、单向应力状态的变形比能s1§8－6复杂应力状态下的变形比能变形能：物体由于变形而积储的能量。变形比能：单位体积积储的变形能 231图a图c3-m1-m2-mm图bmm二.三向应力状态下的比能三.体积改变比能和形状改变比能 231图a图c3-m1-m2-mm图bmm体积改变比能 称为形状改变比能或歪形能。图c3-m1-m2-m 例用能量法证明三个弹性常数间的关系：纯剪单元体的比能为：纯剪单元体比能的主应力表示为：txyA13 （拉压）（弯曲）（正应力强度条件）（弯曲）（扭转）（剪应力强度条件）1.杆件基本变形下的强度条件§8–8强度理论的概念上面强度条件没有考虑材料的破坏原因，而是直接根据试验结果建立的强度条件。这只对危险截面上危险点处是单向应力状态或纯剪应力状态这类特殊情况才适用。 2、复杂应力状态的危险点如何建立强度条件？mP工程中的受力构件，当承载达到一定程度时，其材料一般会在构件危险截面上的危险点处首先发生屈服或裂开而进入危险状态。为了保证构件能够正常工作，须建立强度条件。那么，对这样的单元体如何建立强度条件呢？如果还象单向拉伸（单向应力状态）一样，靠实验来确定失效状态、建立强度条件，则必须对各式各样的应力状态一一进行实验，这是难以实现的。 3.构件由于强度不足而引起的两种失效（破坏）形式(1)脆性断裂：以出现裂纹或断裂为破坏标志。(2)塑性屈服（流动）：以产生过大塑性变形为破坏标志。4.强度理论：人们根据大量的破坏现象，通过判断推理、概括，提出了种种关于材料破坏原因的假说，并找出引起破坏的主要因素，经过实践检验，不断完善，在一定范围与实际相符合，上升为理论。强度理论是关于“构件发生强度失效起因”的假说。解决这类问题，往往是依据部分实验的结果，经过推理，提出一些假说，推测材料强度失效的原因，从而建立强度条件。 §8–9四个强度理论一、最大拉应力（第一强度）理论：此理论认为最大拉应力是引起材料脆性断裂的主要原因。即危险点无论在什么应力状态下，只要三个主应力中的最大拉应力达到材料单向拉伸的极限应力值，材料就发生脆断破坏。1、破坏判据：2、强度准则：3、实用范围：实用于破坏形式为脆断的构件。 二、最大伸长线应变（第二强度）理论：1、破坏判据：2、强度准则：3、实用范围：实用于破坏形式为脆断的构件。此理论认为最大伸长线应变是引起材料脆性断裂的主要原因。即危险点无论在什么应力状态下，只要最大伸长线应变达到材料单向拉伸时的极限应变值，材料就发生脆断破坏。 三、最大剪应力（第三强度）理论：1、破坏判据：3、实用范围：实用于破坏形式为屈服的构件。2、强度准则：此理论认为最大剪应力是引起材料发生塑性屈服的主要原因。即危险点无论在什么应力状态下，只要最大剪应力达到单向拉伸材料屈服时的极限剪应力值，材料就发生屈服破坏。 四、形状改变比能（第四强度）理论：1、破坏判据：2、强度准则3、实用范围：实用于破坏形式为屈服的构件。此理论认为形状改变比能是材料发生塑性屈服的主要原因。即危险点无论在什么应力状态下，只要形状改变比能达到单向拉伸屈服时的形状改变比能，材料就发生屈服破坏。 五.相当应力：（强度准则的统一形式）。其中，—相当应力。 平面应力状态特例（y=0)已知：和试写出最大剪应力理论（第三强度理论）和形状改变比能理论（第四强度理论）的相当应力的表达式。 解：首先确定主应力2＝0 最大剪应力理论形状改变比能理论r4==2＋322＝0(8.5-7)(8.5-8) 例校核K点的强度。已知：＞[]=170MPasr4==197MPa＞[]结论：K点不满足强度条件，此梁不满足强度要求。s=149.5MPa,t=74.1MPa,120280148.5zy14K2＋32[]=170MPa 强度计算的步骤：1、内力分析，确定可能的危险面。2、应力分析，确定危险点并画出单元体，4、选择适当的强度理论，计算相当应力，然后进行强度计算。强度理论的应用六、强度理论的应用3、求主应力 解：危险点A的应力状态如图：例1直径为d=0.1m的圆杆受力如图,m=7kNm,P=50kN,为铸铁构件，[]=40MPa,试用第一强度理论校核杆的强度。故，安全。PPmmAAst强度理论的应用 例2薄壁圆筒受最大内压时,测得x=1.8810-4,y=7.3710-4,已知钢的E=210GPa，[]=170MPa,泊松比=0.3，试用第三强度理论校核其强度。解：由广义虎克定律得:AsxsyxyA所以，此容器不满足第三强度理论。不安全。强度理论的应用