应力状态(I)--水电、土木

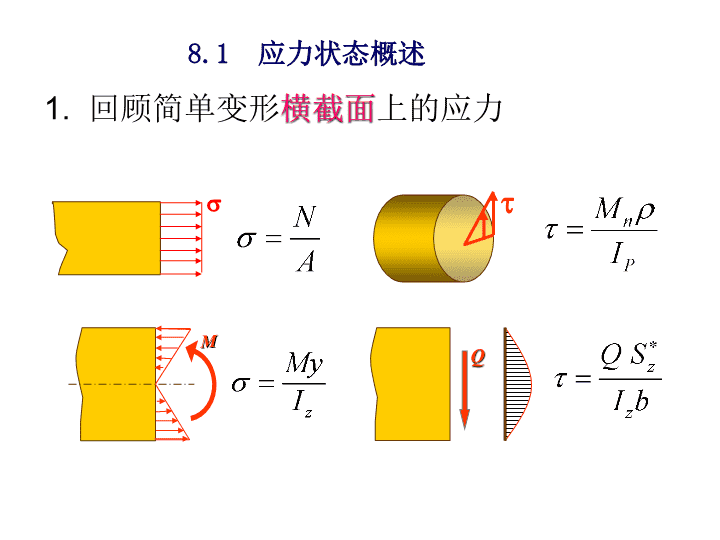
第八章应力状态分析与强度理论 8.1应力状态概述8.2二向应力状态分析8.3二向应力状态的应力圆8.4三向应力状态简介8.5广义胡克定律8.6复杂应力状态的变形比能8.7强度理论概述8.8四种强度理论内容 1.回顾简单变形横截面上的应力MQst8.1应力状态概述 2.斜截面上的应力是否需要研究？低碳钢扭低碳钢拉铸铁扭铸铁拉当然要研究！ 用什么方法研究斜截面上的应力？是否还要用研究横截面上应力一样的方法？ FF拉压杆斜截面上的应力FFpα=σcosαFpα但对于扭转、弯曲及其它受力复杂的杆件，变形后斜截面不再是平面，故研究这些构件上某一点斜方位面上的应力时就不能用斜截面把整个构件截开的方法，只能把构件上的这一点拿出单独进行分析。 过一点不同方向面上应力的情况，称为这一点的应力状态。3、一点的应力状态的概念 单元体：围绕构件上一点取出的一个边长为无穷小（分别为dx,dy,dz）的正六面体。（4）相互垂直两面上剪应力满足剪切双生互等定理。（3）相互平行面上的正应力同为拉或同为压，且数值相等；（2）各面应力均匀分布；（1）dx,dy,dz→0dydxdz4、研究一点应力状态的方法（单元体法）5、单元体的特点zxy应力单元体 单元体的取法：原则：各表面应力已知或可求。113223 FlaS截面内力：S弯矩M=Fl扭矩Mn=Fa剪力Q=F（剪力Q产生的剪应力忽略掉） zxy123MQMn123S横截面横截面 6、主平面(Principalplane)单元体上剪应力为零的平面7、主应力(Principalstress)主平面上的正应力说明:通过构件任一点都可找到三个相互垂直的主平面，三个主平面上的主应力分别记为1,2,3，且规定按代数值的大小顺序来排列,即结论：三个主应力中，有一个是通过这一点所有斜截面上正应力的最大值，有一个是最小值。 8、主单元体（各侧面上剪应力均为零的单元体）围绕一点沿主平面方位截取出的单元体。123 单向应力状态——三个主应力中只有一个主应力不为零。简化9、应力状态的分类二向（平面）应力状态——有两个主应力不为零。σ2σ1σ1σ2简化σ1σ2σ2σ1 三向（空间）应力状态——三个主应力都不为零。σ1σ3σ2 例题1画出如图所示梁S截面(紧邻F左侧）1-5点的应力状态单元体.54321Fl/2l/2Fl/2l/2S截面 S平面254321543211x1x1x2x222333 例题2分析薄壁圆筒受内压时的应力状态pDyz薄壁圆筒的横截面面积mmnpD′nn(1)沿圆筒轴线作用于筒底的总压力为F 直径平面(2)假想用一直径平面将圆筒截分为二，并取下半环为研究对象p"yONNd" xxyzyxyyxxyxyyx一、平面应力状态的一般情形8.2二向（平面）应力状态分析（解析法） xyaxxyxxyxefnefaxxyyxyαααnα二、斜截面上的应力已知：xyyyxy斜截面上的应力ααα求： α正、负号规定——自x轴正向逆时针转到α面外法线n时，α角规定为正，反之为负。应力的正负号规定：正应力------拉为正，压为负xαn剪应力------使研究对象有沿顺时针方向转动趋势者为正，逆时针为负。 求任意斜截面上应力的方法：平衡方程xααntαfae假想地沿斜截面ef将单元体截开,留下左边部分的脱离体eaf作为研究对象xyaxxyxxyxefnyy xααnteaf设ef的面积为,则： xααnt 整理后得到有界、周期函数 将上式对α求导数，并令其等于零，有由此解出角度0和0+90°0和0+90°确定两个互相垂直的平面，一个是最大正应力所在的平面，另一个是最小正应力所在的平面.考查一下正应力的极值三、正应力的极值（max，min） 将0和0+90°代入公式得到max和min确定正应力的极值大小由 故max和min作用平面上剪应力为零，此平面就是主平面，max和min就是主应力，即max=1min=2四、主平面、主应力而故由解出的角度0和0+90°为主平面的方位。 (1)当x>y时，则1偏向x，2偏向y(2)当x<y时，则1偏向y，2偏向x(3)当x=y时，0=45°，主应力的方向可由单元体上剪应力情况直观判断出来则确定主应力方向的具体规则如下：下面还必须进一步判断0是x与哪一个主应力间的夹角大偏大，小偏小的原则若约定|0|<45°即0取值在±45°范围内，即0是x与1之间的夹角，即0是x与2之间的夹角 1、最大剪应力作用面的方位令1和1+90°确定两个互相垂直的平面，一个是最大剪应力所在的平面，另一个是最小剪应力所在的平面.五、最大剪应力及其作用面方位 2、最大剪应力将1和1+90°代入公式得到max和min由和知最大剪应力与最大正应力作用面方位的关系 需要特别指出的是，上述剪应力极值仅对垂直于主应力为零的平面(xy坐标面）的方向面而言，因而称为面内最大剪应力与面内最小剪应力。二者不一定是过一点的所有方向面中剪应力的最大和最小值。xyz xyxy图示单元体，已知x=-40MPa，y=60MPa，xy=-50MPa.试求ef截面上的应力情况及主应力和主平面的方位.n30°ef(1)求ef截面上的应力例题1 (3)求主平面的方位x=-40MPay=60MPax=-50MPa=-30°因为x<y，所以0=-22.5°与2对应(2)求主应力的大小 xyxy22.5°12 两端简支的焊接工字钢梁及其荷载如图所示，梁的横截面尺寸示于图中。试求出紧邻集中力的左侧C截面上a,b两点处的主应力，并求出主平面的方位。12015152709zab250KN1.6m2mABC例题2 +200kN50kN+80kN.m解:(1)首先计算支反力,并作出梁的剪力图和弯矩图Mc-=MC=80kN•mQc-=200kN250KN1.6m2mABC 12015152709zab(2)横截面上a点的应力为a点的单元体如图所示axxxyyx x=a=122.5MPa，xy=a=64.6MPay=0，yx=-64.6MPaaxxxyyx(3)a点的主应力大小(4)a点的主平面方位axxxyyx012 12015152709zab(5)横截面上b点的应力b点的单元体如图所示bxx b点的两个主应力为1所在的主平面就是x平面。bxx 练习题：分析圆轴扭转时最大正应力的作用面，说明铸铁圆试样扭转破坏的主要原因。铸铁圆试样扭转试验时，正是沿着最大拉应力作用面（即45o螺旋面）断开的。因此，可以认为这种脆性破坏是由最大拉应力引起的。A 练习题：分析轴向拉伸杆件的最大剪应力的作用面，说明低碳钢拉伸时发生屈服的主要原因。低碳钢试样拉伸至屈服时沿45o表面出现滑移线，是由最大剪应力引起的。 §8.3二向（平面）应力状态分析——图解法对上述方程消去参数（2），得：一、应力圆方程xysxtxysyOsytxysxsataaxyOtn此方程曲线为圆—应力圆（或莫尔圆，由德国工程师：OttoMohr引入） RCO圆心（，0）半径一点应力状态的另一种表示方法建立座标系如图示圆上一点的坐标对应着单元体某一斜截面上的应力。 建立应力坐标系，如下图所示，（注意选好比例尺）二、画应力圆的步骤：在坐标系内确定点A(x，xy)和B(y，yx)连接AB，其与s轴的交点C便是圆心。以C为圆心，以AC为半径画圆——应力圆；sxtxysyxyOnsataaOstCA(sx,txy)B(sy,tyx)x2anD(sa,ta)tyx sxtxysyxyOnsataaOstCA(sx,txy)B(sy,tyx)x2anD(sa,ta)三、单元体与应力圆的对应关系面上的应力，应力圆上一点坐标(，)单元体上两平面的夹角为，则在应力圆上与两平面上应力所确定的坐标点所夹的圆弧的圆心角为2，且转向一致。 1.主平面主应力OCRD1(σx,τxy)主平面方向主应力四、应力圆的应用AB 2.面内最大剪应力---面内最大剪应力。所在平面与主平面夹角成45°.tsotmaxCs1s2 单向拉伸stsA（s，0）BAB45°e90°E（与σmax成45°角）s1＝σs2＝0 tst90°90°s1＝ts2＝-ts1＝ts2＝-t（与σ1和x轴成45°角）s1＝t45°s2＝-t45°主应力单元体纯剪切 o从水坝体内某点处取出的单元体如图所示,x=-1MPa,y=-0.4MPa,xy=-0.2MPa,yx=0.2MPa,(1)绘出相应的应力圆(2)确定此单元体在=30°和=-40°两斜面上的应力。xyxy解:(1)画应力圆量取OA=x=-1,AD=xy=-0.2,定出D点;ACBOB=y=-0.4，BD′=yx=0.2,定出D′点.(-1,-0.2)DD′(-0.4,0.2)以DD′为直径绘出的圆即为应力圆。例题1 将半径CD逆时针转动2=60°到半径CE,E点的坐标就代表=30°斜截面上的应力。(2)确定=30°斜截面上的应力E60°(3)确定=-40°斜截面上的应力将半径CD顺时针转2=80°到半径CF,F点的坐标就代表=-40°斜截面上的应力。F80°AD′CBoD30°-40°-40°30°-40°=0.26MPa-40°=-0.95MPa30°=-0.36MPa30°=-0.68MPa 两端简支的焊接工字钢梁及其荷载如图所示，梁的横截面尺寸示于图中。试绘出紧邻c左侧截面上a,b两点处的应力圆，并用应力圆求出这两点处的主应力。12015152709zab250KN1.6m2mABC例题2 +200kN50kN+80kN.m解:(1)首先计算支反力,并作出梁的剪力图和弯矩图Mc-=MC=80kN•mQc-=200kN250KN1.6m2mABC 12015152709zab(2)横截面上a点的应力为a点的单元体如图所示axxxyyx 由x，xy定出D点由y，yx定出D′点以DD′为直径作应力圆OC(3)作应力圆x=a=122.5MPa，xy=a=64.6MPay=0，yx=-64.6MPaAB(122.5,64.6)D(0,-64.6)D′A112A2A1，A2两点的横坐标分别代表a点的两个主应力1和3A1点对应于单元体上1所在的主平面 axxxyyx01212015152709zab(4)横截面上b点的应力b点的单元体如图所示bxx b点的两个主应力为1所在的主平面就是x平面。bxx(136.5,0)D(0,0)D′1