钢筋混凝土PPT课件

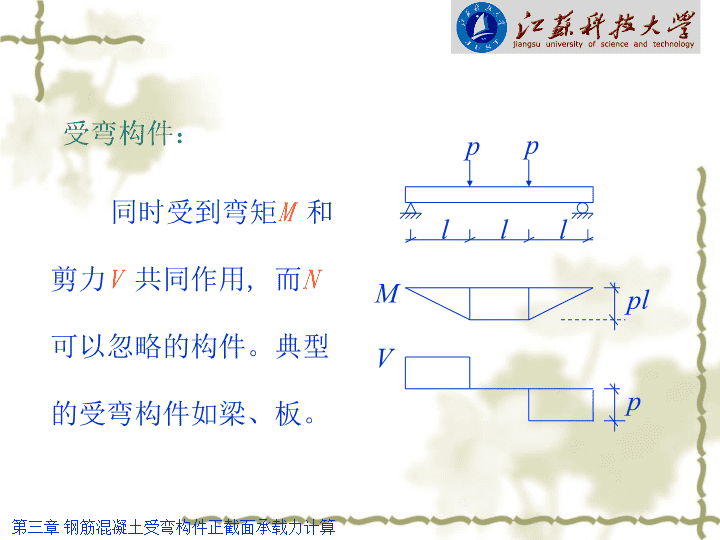
第三章受弯构件正截面承载力计算FlexureStrengthofRCBeams 主要内容第一节受弯构件的截面形式和构造第二节受弯构件的正截面试验研究第三节正截面受弯承载力计算原则第四节单筋矩形截面构件正截面承载力计算第五节双筋矩形截面构件正截面承载力计算第六节T形矩形截面构件正截面承载力计算第七节受弯构件的延性 受弯构件：同时受到弯矩M和剪力V共同作用,而N可以忽略的构件。典型的受弯构件如梁、板。pplllMplVp 受弯构件的破坏情况在弯矩作用下发生正截面受弯破坏；在弯矩和剪力共同作用下发生斜截面受剪或受弯破坏。 bhl0纵向钢筋★正截面受弯承载力设计——为防止正截面破坏，须配纵向钢筋。 ★斜截面受剪承载力设计——为防止斜截面破坏，须配弯起钢筋及箍筋。bh纵向钢筋l0箍筋架力钢筋 一.截面形式第一节受弯构件的截面形式和构造梁截面形式常见的有矩形、T形、工形、十字形、箱形、Π形。现浇单向板为矩形截面，预制板常见的有空心板。单筋截面和双筋截面工形矩形板矩形T形箱形空心板 二.截面尺寸为统一模板尺寸、便于施工，通常采用梁宽度b=120、150、180、200、220、250mm，250mm以上者以50mm为模数递增。梁高度h=250、300、350、400、…800mm，800mm以上者以100mm为模数递增。简支梁的高跨比h/l0一般为1/8~1/12。矩形截面梁高宽比h/b=2.0~3.5，T形截面梁高宽比h/b=2.5~4.0。房屋建筑中板较薄，最小为60mm。水工建筑中板厚变化范围大，厚的可达几米，薄的可为100mm。bhbh 三.砼保护层c不小于钢筋直径附录4表1粗骨料最大粒径的1.25倍混凝土保护层厚度为保证耐久性、防火性以及钢筋与砼的粘结性能，钢筋外面须有足够厚度的砼保护层。 四.梁内钢筋直径和间距Sn梁底部纵向受力钢筋一般不少于2根，直径常用10-28mm；梁上部无受压钢筋时，需配置2根架立筋，与箍筋和梁底部纵筋形成钢筋骨架，直径一般不小于10mm；共同受力钢筋直径相差不大于4mm。 d=10~28mm(常用)h0=h-a为保证砼浇注的密实性，梁底部钢筋的净距不小于25mm及钢筋直径d，梁上部钢筋的净距不小于30mm及1.5d。h0acccc25mmdSnSnSn..............1.5dSn25mmd1.25D1.5D 五.板内钢筋的直径和间距钢筋直径通常为6~12mm，板厚度较大时，直径常用14~18mm；受力钢筋最小间距为70mm；最大间距P57。垂直于受力钢筋应布置分布钢筋。布于受力钢筋内侧，直径6~8mm，间距250mm。厚板分布钢筋直径10~16mm，间距200~400mm。≥70mmC≥cmin分布钢筋(f6@300)h0 分布钢筋的作用将荷载均匀传递给受力钢筋；施工中固定受力钢筋的位置；抵抗温度和收缩产生的应力；抵抗另一方向的内力。每米板宽中分布钢筋面积不少于受力钢筋面积的15%。 第二节受弯构件正截面的试验研究habAsh0一．梁的试验和应力—应变阶段 适筋梁试验动画 0.40.60.81.0ⅠaⅡaⅢaⅠⅡⅢMcrMyMu0fM/Mu适筋截面受力的三个阶段整个加载过程，平均应变符合平截面假定。 荷载很小，应力与应变之间成线性关系；荷载↑，砼拉应力达到ft，拉区呈塑性变形；压区应力图接近三角形；砼达到极限拉应变t=tu，截面即将开裂（Ⅰa状态），弯矩为开裂弯矩Mcr；Ⅰa状态是抗裂计算依据。第Ⅰ阶段—未裂阶段sAsItmaxMcrIaftk 荷载↑，拉区出现裂缝，中和轴上移，拉区砼脱离工作，拉力由钢筋承担。阶段Ⅱ是正常使用阶段变形和裂缝宽度计算依据。拉区有许多裂缝，纵向应变量测标距有足够长度（跨过几条裂缝），平均应变沿截面高度分布近似直线。（平截面假定）第Ⅱ阶段—裂缝阶段yMyfyAsIIasAsII 荷载↑，钢筋应力先达到屈服强度fy；压区砼边缘应变随后达到极限压应变cu，砼发生纵向水平裂缝压碎（Ⅲ状态），弯矩为极限弯矩Mu。阶段Ⅲ是正截面承载力计算依据。第Ⅲ阶段—破坏阶段cmaxMufyAs=ZDx0IIIaMfyAsIIIZ 二、正截面破坏特征适筋破坏超筋破坏少筋破坏 适筋破坏配筋量适中；受拉钢筋先屈服，然后砼边缘达到极限压应变εcu，砼被压碎，构件破坏。破坏前，有显著的裂缝开展和挠度，有明显的破坏预兆，属延性破坏。 超筋破坏配筋量过多;受拉钢筋未达到屈服，受压砼先达到极限压应变而被压坏。承载力控制于砼受压区，钢筋未能充分发挥作用。裂缝根数多、宽度细，挠度也比较小，砼压坏前无明显预兆，属脆性破坏。 少筋破坏配筋量过少;拉区砼一出现裂缝，钢筋很快达到屈服，可能经过流幅段进入强化段。破坏时常出现一条很宽裂缝，挠度很大，不能正常使用。开裂弯矩是其破坏弯矩，属于脆性破坏。 配筋量太少，破坏弯矩接近开裂弯矩，大小取决于砼的抗拉强度及截面大小；配筋量过多，钢筋不能充分发挥作用，破坏弯矩取决于砼的抗压强度及截面大小；合理的配筋应在这两个限度之间，避免发生超筋或少筋破坏。破坏特征随配筋量变化 第三节正截面受弯承载力计算原则（1）平截面假定。（2）不考虑受拉区砼的工作。（3）受压区砼采用理想化的应力应变曲线。（4）有明显屈服点的钢筋应力应变关系采用理想的弹塑性曲线。一、计算方法的基本假定 计算方法的基本假定cu0fc0砼0fyy钢筋 等效矩形应力图用等效矩形应力图形代替曲线应力图形，应力为fc。根据合力大小和作用点位置不变的原则：受压砼的应力图形从实际应力图等效矩形应力图理想应力图DDDMuMuMuAsfyAsfyAsfy实际应力图理想应力图计算应力图x0x0x 界限破坏：受拉钢筋达到屈服强度的同时受压砼达到极限压应变，此时：二．适筋和超筋破坏的界限条件相对受压区高度： cuh0s>yn<nbn>nbh0nbh0ys<y根据平截面假定： ★适筋梁的判别条件表3-1适筋梁超筋梁系数，DL规范为1.0，SL规范为0.85。 三、适筋梁与少筋梁的界限最小配筋率ρmin：按Ⅲa阶段计算的正截面受弯承载力与由素混凝土受弯构件计算得到正截面承载力相等。配筋率：h0haAsb 第四节单筋矩形截面构件正截面受弯承载力计算一．计算简图fyAsMufcx/2Cxh0二.基本公式 为计算方便，基本公式改写如下： 1.防止超筋脆性破坏2.防止少筋脆性破坏公式适用条件 已知：弯矩设计值M求：截面尺寸b，h(h0)、截面配筋As，以及材料强度fy、fc未知数：受压区高度x、As、b，h(h0)、fy、fc基本公式：根据受力性能、材料供应、施工条件、使用要求等因素综合分析，确定经济合理的设计。三.截面设计没有唯一解! 截面尺寸确定●截面应有一定刚度，使正常使用阶段的验算能满足挠度变形的要求。●根据工程经验，常按高跨比h/l0来估计截面高度：简支梁可取h=(1/8～1/12)l0，b=(1/2～1/3.5)h；简支板可取h=(1/12～1/35)l0。 对一般板和梁，其常用（经济）配筋率为：板0.4%～0.8%矩形截面梁0.6%～1.5%T形截面梁0.9%～1.8%（相对于梁肋来说）截面尺寸b、h越大，所需的As就越少，越小，但砼用量和模板费用增加，并影响使用净空高度；反之，b、h越小，所需的As就越大，增大。 正截面抗弯钢筋的设计步骤1做出计算简图支座的情况、荷载大小、计算跨度2内力计算求出荷载效应MD3配筋计算1）计算αs，计算ξ，判断是否超筋，是超筋则加大截面尺寸或双筋截面。2）不是超筋则计算钢筋面积，判断是否少筋，是则按最小配筋率配筋。适当考虑经济配筋率。3）选取钢筋直径和布置钢筋，绘制配筋图。 已知：截面尺寸b，h、截面配筋As，以及材料强度fy、fc求：截面的受弯承载力Mu未知数：受压区高度x和受弯承载力Mu基本公式：四、承载力复核 已知：、、、、、、求：未知数：、基本公式：（1）当且时，用基本公式直接计算；（2）当时，说明是超筋梁，取，；（3）当时，说明是少筋梁，分别按素混凝土构件和钢筋混凝土构件计算，取小值。 【回顾】1.正截面破坏三种形式超筋破坏少筋破坏适筋破坏 截面设计步骤已知M,b,h,fc,ft是否求出As是否调整b,h或fc 截面验算步骤已知M,As,b,h,fc,ft是否是否调整b,h,As 第五节双筋矩形截面构件正截面受弯承载力计算双筋截面是指同时配置受拉和受压钢筋的情况。 工程中通常仅在以下情况下采用双筋截面：截面尺寸和材料强度受建筑使用和施工条件限制而不能增加，而计算又不满足适筋截面条件时，可采用双筋截面。由于荷载有多种组合情况，在某一组合情况下截面承受正弯矩，另一种组合情况下承受负弯矩，这时也出现双筋截面。由于受压钢筋可以提高截面的延性，在抗震地区，一般宜配置受压钢筋。 一．计算简图和基本公式MAsfyAsfyAsAsfcbh0xx受压钢筋的应变接近0.002，故其应力达到屈服强度 ●防止超筋脆性破坏●保证受压钢筋强度充分利用:为使受压钢筋距中和轴足够远，得到足够变形，应力才能达到屈服强度。双筋截面一般不会出现少筋破坏情况，故可不必验算最小配筋率。适用条件 受压钢筋应力达不到屈服强度，假定受压钢筋和砼的压力作用点均在钢筋重心位置当时，令fyAs1Mu1fcCxAsbh0a 二．截面设计（一）第一种情况已知：弯矩设计值M，截面尺寸b，h(h0)，材料强度fy、fc未知数：受压区高度x、截面配筋As’，As基本公式：两个方程，三个未知数，根据充分利用受压区砼受压使钢筋用量（As’+As）为最小原则，取x=xb，截面配筋可求。 （二）第二种情况已知：弯矩设计值M，截面尺寸b，h(h0)，材料强度fy、fc，受压钢筋截面面积As’未知数：受压区高度x、受拉钢筋As基本公式：两个方程，两个未知数，受拉钢筋As可求。如何处理？如何处理？ 三.承载力复核已知：b、h、a、a’、As、As’、fy、fy’、fc求：Mu未知数：受压区高度x和受弯承载力Mu两个未知数，有唯一解。问题：当x>xb时，Mu=?当x<2a’时，Mu=?可偏于安全的按下式计算 三、基本公式应用截面设计步骤已知M,b,h,fc,fy,fy’,A’S是否求出As,A’s是否是否 第六节T形截面构件正截面受弯承载力计算节省砼，减轻自重。挖去受拉区砼，形成T形截面，对受弯承载力没有影响。 受拉钢筋较多，可将截面底部适当增大，形成工形截面。工形截面的受弯承载力的计算与T形截面相同。 AABBA—AB—B跨中A按？截面设计；支座B按？截面设计。 受压翼缘越大，对截面受弯越有利（x减小，内力臂增大）。试验和理论分析均表明，整个受压翼缘砼的压应力分布是不均匀的。距腹板距离越远，压应力越小。 采用翼缘计算宽度bf’；在bf’范围内假定压应力均匀分布；bf’与翼缘高度h’f、梁的跨度l0、受力情况等因素有关。简化方法：实际应力图块实际中和轴有效翼缘宽度等效应力图块bf 计算翼缘宽度 第一种情况防止超筋脆性破坏，应满足x≤bh0。第一类T形截面，该适用条件一般能满足。防止少筋脆性破坏，应满足≥min，=As/bh0，b为T形截面的腹板宽度。一、计算简图和基本公式第一类T形截面 第二种情况防止超筋脆性破坏，应满足：防止少筋脆性破坏，应满足：≥min第二类T形截面，该条件一般能满足。第二类T形截面 第一类T形截面第二类T形截面界限情况T形梁类型判别 截面设计1判别T形梁类型2第一类T形梁按宽度等于bf’的矩形截面设计。3第二类T形梁计算方法：考虑T型翼缘混凝土的受压作用，按相应公式计算。 承载力复核1判别T形梁类型2第一类T形梁按宽度等于bf’的矩形截面复核。3第二类T形梁，考虑翼缘混凝土的受压作用。 已知M,bf’,hf’,b,h,fc,fy是否是求出As是否是加大b,h或fc否加大b,h或fc否第一类Ｔ形截面第二类Ｔ形截面配受压钢筋截面设计步骤 第七节受弯构件的延性设计构件除了考虑截面破坏强度，构件还应满足一定的延性要求。延性是指结构构件或截面受力超过弹性阶段后，在承载力无显著变化的情况下的后期变形能力。因此，延性即结构构件或截面最终破坏之前经受非弹性变形的能力。 延性对结构构件的影响延性好的结构破坏过程比较长，破坏前有明显的预兆。便于及早采取措施，避免事故发生及结构崩溃。延性差的结构，发生脆性破坏，破坏后果较为严重。延性好的超静定结构破坏前的内力重分布可以增加结构的极限荷载。延性好的结构能以残余塑性变形吸收地震作用产生的巨大能量，这对地震区的工程结构极为重要。对抗震结构，延性至少是与强度同等重要的！ 截面延性截面延性是指以截面性质定义的后期变形能力，通常以曲率的比值(u/y)表示，称为曲率延性系数=u/y。y为受拉钢筋屈服时的截面曲率；u为混凝土最终被压碎时的截面曲率，即构件最终破坏时的截面曲率。 位移延性系数对于整个结构来说，延性应该用整个结构的变形来衡量，通常以位移延性系数=u/y表示。对于钢筋混凝土结构，为抵抗强震，常要求不小于3—5。应注意在数值上与截面的曲率延性系数是完全不同的。 影响截面延性的因素截面受压区高度混凝土极限压应变影响受弯构件延性的因素纵向钢筋用量混凝土强度和钢筋强度箍筋用量 本章重点受弯构件三种破坏形态：少筋破坏、适筋破坏、超筋破坏适筋破坏的三个阶段：弹性阶段、带裂缝工作阶段、破坏阶段正截面承载力计算公式及公式适用条件单筋矩形截面、双筋矩形截面、T型截面截面设计与承载力验算钢筋混凝受弯构件的延性及影响因素