岩土力学课件--第三章土体中的应力计算

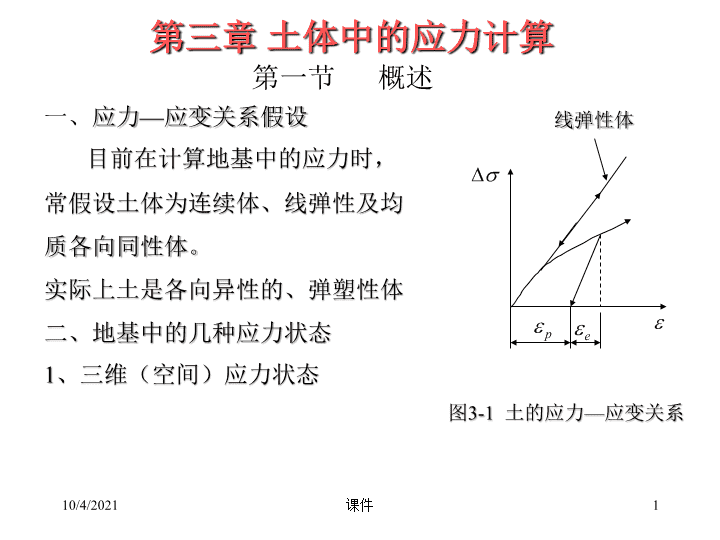
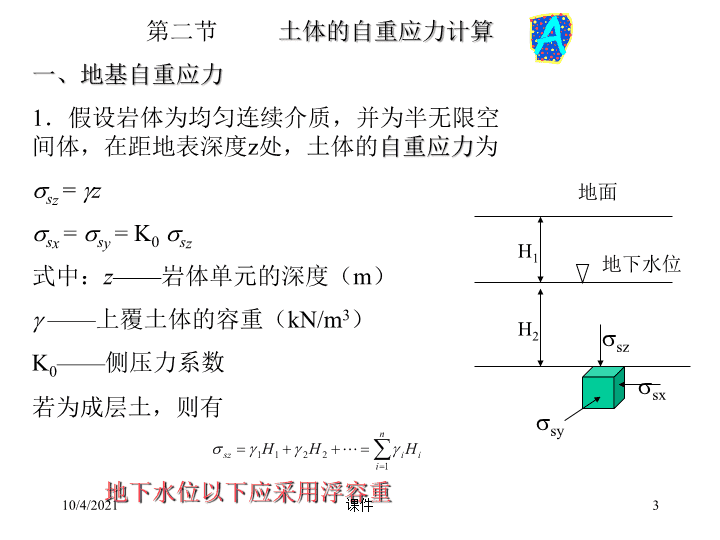
第三章土体中的应力计算第一节概述一、应力—应变关系假设目前在计算地基中的应力时，常假设土体为连续体、线弹性及均质各向同性体。实际上土是各向异性的、弹塑性体二、地基中的几种应力状态1、三维（空间）应力状态线弹性体图3-1土的应力—应变关系10/4/20211课件 1、三维（空间）应力状态2、二维（空间）应力状态3、侧限应力状态二、土力学中应力符号规定压为正，拉为负，剪应力以逆时针为正。zzxy图3-5侧限应力状态地面10/4/20212课件 第二节土体的自重应力计算一、地基自重应力1．假设岩体为均匀连续介质，并为半无限空间体，在距地表深度z处，土体的自重应力为sz=zsx=sy=K0sz式中：z——岩体单元的深度（m）——上覆土体的容重（kN/m3）K0——侧压力系数若为成层土，则有地下水位以下应采用浮容重sx地面H1H2szsy地下水位10/4/20213课件 若岩体视为各向同性的弹性体，x=y=0，sx=sy由广义虎克定律x=1/E[x-（y+z）]=0y=1/E[y-（x+z）]=0由此得：x=y=/（1-）z=/（1-）H（3-5）所以，侧压力系数K0=/（1-）K0和与土的种类、密度有关，可由试验确定，或查表4-2二、土坝的自重应力10/4/20214课件 第三节基底压力（1）基底接触压力的产生建筑物荷重基础地基上在地基与基础的接触面上产生的压力（地基作用于基础底面的反力）（2）接触压力的大小影响因素地基土和基础的刚度大小荷载大小基础埋深地基土的性质10/4/20215课件 一、基底压力的分布规律（一）基础的刚度的影响弹性地基上的完全柔性基础(EI=0)土坝(堤)、路基、油罐等薄板基础、机场跑道。可认为土坝底部的接触压力分布与土坝的外形轮廓相同,其大小等于各点以上的土柱重量。(图3-35)柔性基础：基底压力的分布形式与作用在它上面的荷载分布形式相一致。基底压力的分布规律10/4/20216课件 弹性地基上的绝对刚性基础(EI=)弹性解:基础两端应力为无穷大实际情况:马鞍形(图3-36)刚性基础：基底压力的分布形式与作用在它上面的荷载分布形式不相一致。10/4/20217课件 弹塑性地基上的有限刚性的基础(0B/6,应力重新分布1/2×L×pmax×3K=Ppmax=2P/(3KL)式中，K=B/2-e10/4/202110课件 2、双向偏心若基底最小压力pmin0,基底最大、最小压力计算公式式中Mx,My—竖直偏心荷载P对基底x,y轴的力矩(kNm);Mx=Pex;My=PeyWx,Wy—基底分别对x,y轴的抵抗矩Wx=BL2/6，(m3)Wy=LB2/610/4/202111课件 整理后得条基：在长度方向取1米即可。三、水平荷载作用矩形：ph=Ph/BL条基：ph=Ph/BL10/4/202112课件 四、基底附加应力(p0)基底处的地基由于建筑物建造后而增加的应力。只有基底附加应力才能引起地基的附加应力和变形。p0d0d0dpFG基坑（槽）基底附加应力p0:显然，若埋深d=0，则基底附加应力等于基底应力，即p0=p1210/4/202113课件 式中p—基底应力，kPa;sz—土中自重应力，基底处sz=0d,kPa;0—基础底面标高以上天然土的加权平均容重，0=（1h1+2h2+……）/(h1+h2+……),其中地下水位以下的容重取浮容重，kN/m3;d—基础埋深，必须从天然地面算起，对于新填土场地则应从老天然地面起算，d=h1+h2+……,m说明：当基坑的平面尺寸和深度较大时，坑底回弹是明显的，在沉降计算中，为适当考虑这种坑底的回弹和再压缩而增加的沉降，，改取p0=p-sz其中为0~1的系数（《地基及基础》华南理工大学等编，中国建筑工业出版社，45~）10/4/202114课件 第四节地基中的附加应力计算地基附加应力：指建筑物荷重在土体中引起的附加于原有应力之上的应力。计算方法假设：1、将地基看成是均质的线性变形半空间，直接采用弹性力学解答2、将基底压力看成是柔性荷载，而不考虑基础刚度的影响一、集中荷载作用下的附加应力计算（一）、竖直集中力作用——布辛内斯克解布辛内斯克根据弹性理论计算出地基下某一点M的6个应力分量和三个位移分量。由于对地基沉降意义最大的是竖向法向应力z，只研究z10/4/202115课件 （3-8）K称为集中应力系数讨论z的分布特征：1、沿P作用线方向，z随深度而减小；2、r>0的竖向线上，z，z：0增大减小3、z=cost在P处最大，随r，z结论：集中力P在地基中引起的附加应力的分布是向下、向四周无限扩散开的。10/4/202116课件 （二）、水平集中力作用—西罗克课题西罗克弹性理论解二、矩形面积上各种分布荷载作用下的附加应力计算（一）、矩形面积竖直均布荷载角点下应力集中荷载dP=dxdyp0,M点处dz为10/4/202117课件 式中Ks——_为矩形竖向均布荷载角点下的应力分布系数Ks=f(L,B,z),(注意:B为荷载面的短边宽度),可从表3-2中查得。2、任一点的应力—角点法(a）M/在荷载面的边缘z=z1+z2M/在荷载面内部z=z1+z2+z3+z4M/1212344312M/M/(a)(b)(c)10/4/202118课件 （c）M/在荷载面外部z=z3+z4-z1-z2（二）、矩形面积竖直三角形荷载dP在O点下任意M处引起的竖直附加应力dzz=Ktpt注：求O/点下的应力时，可用竖向均布荷载与竖直三角形荷载叠加。10/4/202119课件 （三）、矩形面积水平均布荷载由西罗克课题，得矩形角点下任意深度z处的附加应力z：式中Kh为系数,可查表3-4三、条形面积上各种分布荷载作用下的附加应力计算平面问题假设：1、宽度B内荷载沿长度L不变2、L5B3、纵轴方向无位移4、变形发生在横截面平面内10/4/202120课件 （一）竖直线布荷载将看成是集中力，则在地基内M点引起的应力按（3-8）得：（3-19）同理，式中，——单位长度上的线荷载(kN/m)10/4/202121课件 (二)、条形面积竖直均布荷载取微段，，视为线布荷载，在地基内M点引起的应力按（3-19）为（3-23）将（3-23）沿宽度B积分，可得整个条形荷载M点引起的附加应力同理10/4/202122课件 三、条形面积上其它分布荷载详见表3-6四、圆形面积竖直均布荷载作用时中心点下的附加应力计算dp在M点引起的附加应力dz由（3-6a）为：在整个圆面积上积分：五、感应图法求不规则面积上竖直均布荷载作用下的附加应力10/4/202123课件 六、影响土中应力分布的因素（一）、非线性材料的影响（二）、双层地基的影响1、可压缩土层覆盖于刚性岩层上沿荷载中心线下，地基附加应力发生“应力集中”，与H/B成反比。2、硬土层覆盖于软土层上荷载中轴线附近，附加应力减小，“应力扩散”。10/4/202124课件 应力扩散随上层厚度的增加而更加显著，它还与双层地基的变形模量E、泊松比有关，即随下列参数f的增加而显著：式中E1，1——上层的变形模量和泊松比；E2，2——软弱下卧层的变形模量和泊松比。由于土的泊松比变化不大（一般=0.3~0.4）,故参数f的大小主要取决于变形模量的比值E1/E2.工程应用:道路路面设计，用坚硬的路面来降低应力集中,减小路面因不均匀变形而破坏10/4/202125课件 第六节应力路径一、应力路径的概念应力历史：土在形成的地质年代中所经受的应力变化情况；剪应力水平（应力水平）：在应力的变化过程中达到的最大剪应力与抗剪强度的比值。（max/f）应力路径：与主应力面成450角斜面在摩尔圆上表示为一点，该点的移动轨迹称为应力路径。为简便，在绘制应力路径时，常把~坐标改换成p~q坐标。10/4/202126课件 土中应力采用总应力表示时：p=1/2*(1+3),q=1/2*(1-3)土中应力采用有效应力表示时(u为孔隙水压力)：p/=p-uq/=q二、几种典型的加载应力路径（一）、没有孔隙水压力的情况初始：1=0，3=C排水固结u=0,/=p=C10/4/202127课件 1、增加周围压力3(图3-60a路径1)初始点：增加后，所以有2、增加偏应力（1-3）(路径2)此时，Copq231图3-60a总应力路径10/4/202128课件 3、增加1相应减少3(图3-60路径3)当试件上1的增加等于3的减少，即时，（二）、有超静孔隙水压力的情况饱和土体在不排水条件下，孔隙水压力的变化,可用孔压系数B和A表示。A与土的性质、应力历史、应力水平等有关。A对有效应力路径的影响()：1、A=0，增加1时不产生孔隙水压力，所以有效应力路径与总应力路径相同，与（一）中情况（2）一样；(图3-60b路径1)10/4/202129课件 2、A=0.5(图3-60b路径2)此时3、A=1.0(图3-60b路径3)则显然:A孔隙水压力u有效应力路径向左上方发展;A孔隙水压力u有效应力路径向右上方发展;CoP/q/123(图3-60b)10/4/202130课件 推广:A不断变化,则有效应力路径成为一根连续发展的曲线应力路径的实际应用:由于土的变形和强度不仅与受力的大小有关，更重要的还与土的应力历史有关，土的应力路径可以模拟土体实际的应力历史，全面地研究应力变化过程对土的力学性质的影响。因此，土的应力路径对进一步探讨土的应力—应变关系和强度都具有十分重要的意义！（详见第五章）10/4/202131课件