理论力学课件 第4章

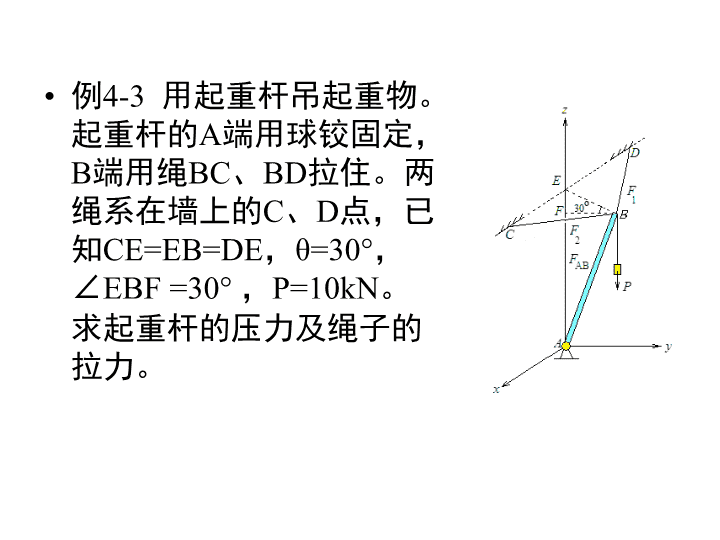
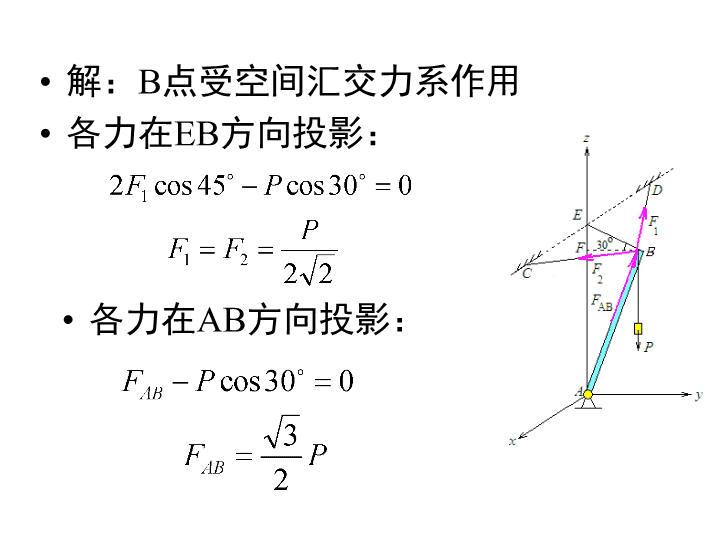
第四章空间力系§4-1空间汇交力系空间汇交力系的合力：FR=F1+F2+…+Fn空间汇交力系的平衡条件： 例4-3用起重杆吊起重物。起重杆的A端用球铰固定，B端用绳BC、BD拉住。两绳系在墙上的C、D点，已知CE=EB=DE，θ=30°，∠EBF=30°，P=10kN。求起重杆的压力及绳子的拉力。 解：B点受空间汇交力系作用各力在EB方向投影：各力在AB方向投影： §4-1力对点的矩和对轴的矩力对点的力矩表示为力矩矢量。1.矢量积设A、B为矢量，定义矢量积A×B：A×B的方向按右手螺旋法确定。 1.力矩矢量 2.坐标矢的矢量积：i×j=kj×k=ik×i=jj×i=-kk×j=-ii×k=-j 3.力对轴的矩设力F的作用点坐标为A(x,y,z)。力的矢量式为：力对轴的矩： 4.力对坐标原点的矩和对坐标轴的矩的关系结论：力对坐标原点的矩在坐标方向的投影等于力对该坐标轴的矩。 §4-3空间力偶1.力偶矩矢量设力F和F’组成一个力偶，其作用点分别为A和B，它们在平面1内。空间力偶矩等于力F与两力距离的乘积。 2.空间力偶等效定理作用在刚体上的两个空间力偶，如果它们的力偶矩矢量相等，则它们对刚体的作用等效。3.空间力偶系的合成。空间力偶系可合成为一个力偶矩。合力偶矩矢等于各个分力偶矩的矢量和。4.空间力偶系的平衡条件： 例4-4工件受到5个力偶的作用，每个力偶矩均为80N.m。求合力偶。解：将5个空间力偶表示为空间矢量：M1=-Mk，M2=-Mj，M3=-Mi，M4=M5=M(-cos45°i-sin45°k)，M=M1+M2+M3+M4+M5+=M[(-1-2cos45°)i-j+(1-2cos45°)k]Mx=-M(1+2cos45°)=-193.14N.mMy=-M=80N.mMz=-M(1+2cos45°)=-193.14N.m §4-4空间任意力系向一点的简化设刚体上作用着n个空间力，F1，F2，…F1n。将各力分别向简化中心O简化，分别得到一个力及一个附加力偶。于是，在点O就得到一个空间汇交力系和一个空间力偶系。主矢F和主矩MO(F)分别为: 关于两个力偶的相加 空间力系的简化结果空间力系向任意一点简化，得到一个主矢和一个主矩。主矢与简化点的位置无关，而主矩则与简化点的位置有关。简化结果有4种情况：1.F=0，MO=0；力系简化成一个力偶。由于力偶矩矢与矩心位置无关，因此，这种情况下，主矩与简化中心的位置无关。 2.F≠0，MO=0；力系简化成一个合力。3.F≠0，MO≠0；一般情况下，力系简化成为一个合力和一个合力偶。特别情况：F≠0，MO≠0；而且有F⊥MO，则还可以进一步简化成一个合力 如果F≠0，MO≠0；而且有F∥MO，则力系简化成所谓的力螺旋。4.F=0，MO=0；空间力系平衡。 §4-5空间任意力系的平衡方程空间任意力系处于平衡的必要、充分条件是：力系的主矢和主矩都等于零。 例4-6均质长方板用6根直杆支持，直杆用球铰与板和地面连接。板重P，在A出作用一个水平力F=2P。求各杆内力。解：设各杆均受拉力。 §4-5重心设物体由若干部分组成，其中第i部分重Pi，则有重心C公式： 重心对于物体为均质，重心C公式为：对于平面图形物体，重心C公式为： 习题4-1在正方形的顶角A和B分别作用力F1和F2，如图所示。求此两力在x,y,z轴上的投影以及对x,y,z轴的矩。并将图中的力系向点O的简化，用解析式表示主矢、主矩的大小和方向。解：先写出力F1和F2的矢量表达式。F1的作用点A(a,a,0) F2的作用点B(0,a,0) 力系向原点O简化：主矢：主矩： 作业4-24-5