建筑结构课件：第3章混凝土结构-受弯2（2012）

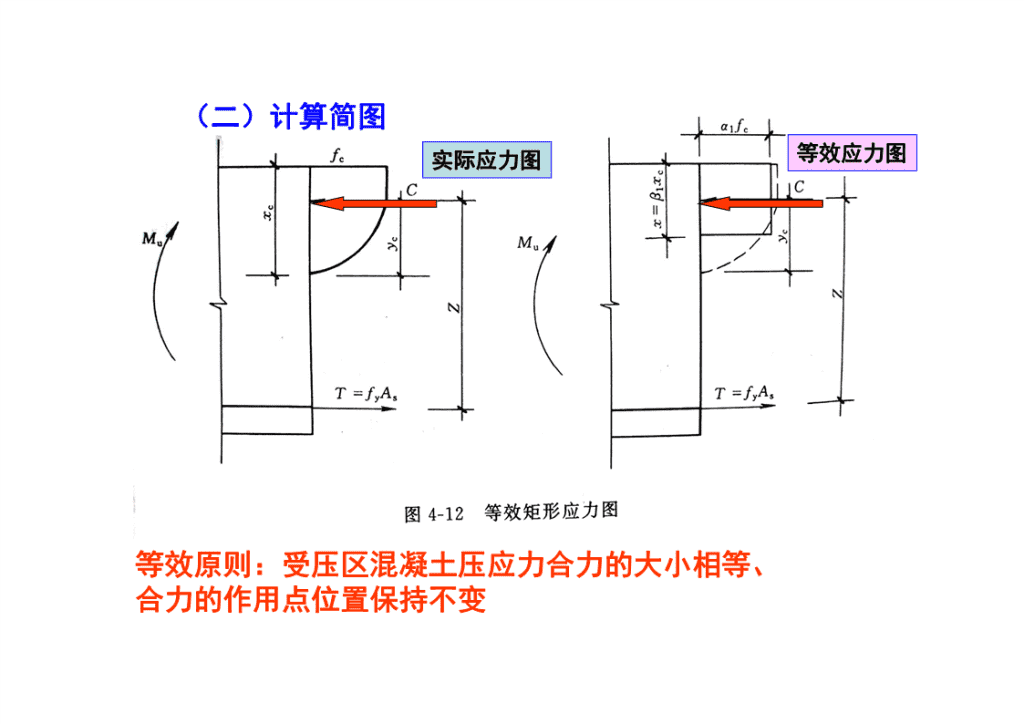
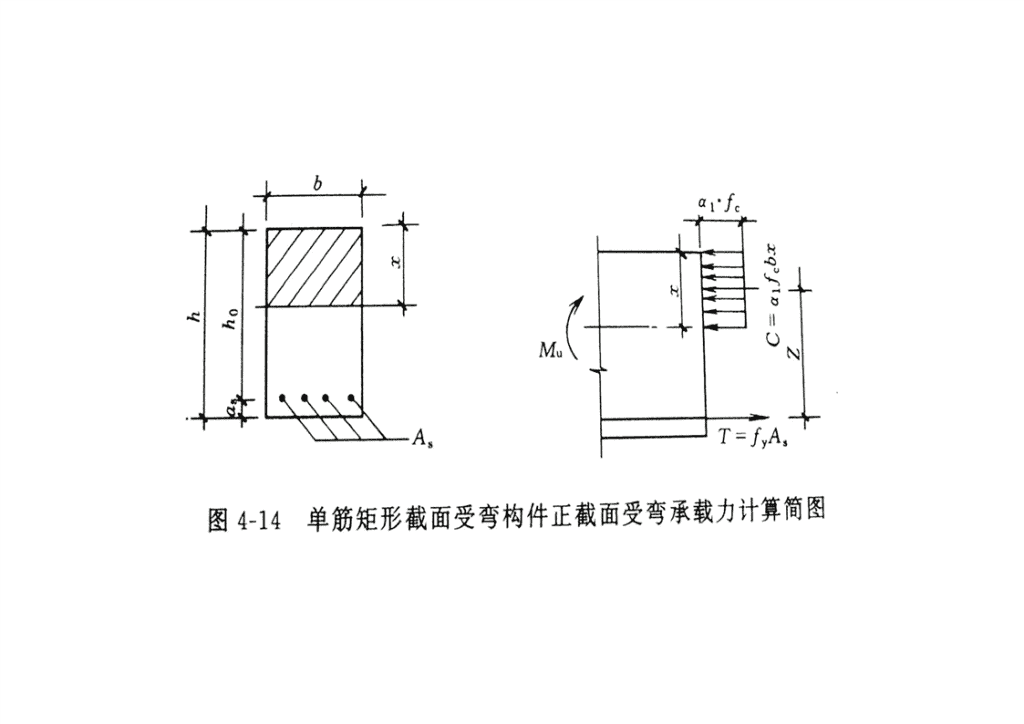
第三章混凝土结构第二节受弯构件的正截面承载力四.单筋矩形截面受弯构件正截面承载力计算（一）基本假定（四个）1.截面应变保持平面（平截面假定）2.不考虑混凝土的抗拉强度（全部拉力由钢筋承受）3.混凝土受压的应力——应变关系为曲线（P45～46）4.纵向钢筋的应力——应变关系方程为σ=Ef⋅≤εsssy （二）计算简图实际应力图等效应力图等效原则：受压区混凝土压应力合力的大小相等、合力的作用点位置保持不变 （三）基本计算公式αfcC=αfcbx采用等效应力图形，根据力的x=βxc平衡：M∑x=0α1fcbx=fyAs力矩的平衡：Ts=fyAs∑M=0M=αfbx(h−0.5x)=fA(h−0.5x)u1c0ys022相对受压区高度M=αfbhξ(1−0.5ξ)=ααfbhu1c01sc0xξ=α=ξ(1−0.5ξ)sh0 （四）适筋梁与超筋梁的界限及界限配筋率适筋梁与超筋梁的界限为“平衡配筋梁”，即梁受拉纵筋屈服的同时，受压混凝土边缘达到其极限压应变εcu值，梁达到其极限承载力而破坏。假设此时的中和轴高度为xcbxεcbcu=hε+ε0cuyxεxxbcu=β=b1cbβhε+ε10cuyx截面应变图fβb1y===ξεybhfEs0y1+Eε界限相对受压高度scuξb 当砼≤C50时，HPB235HRB335HRB4000.6140.5500.518ξbα0.4260.3990.384s,max当ξ≤ξb时，适筋主要是用相对受压区高度来判断是否超筋时，超筋ξ>ξbfc界限配筋率ρ=αξb1bfy （五）适筋梁与少筋梁的界限，最小配筋率少筋梁特点：一裂就坏，即破坏弯矩Mu=开裂弯矩Mcr为防止少筋破坏，构件的配筋率不低于最小配筋率。受拉钢筋的最小配筋率根据破坏弯矩等于开裂弯矩来确定。Asρ=minbhρmin取0.2%和45f/f(%)中的较大值。ty （六）实用计算步骤1.截面设计已知：M，混凝土等级，钢筋级别，b×h，求As解：①根据环境类别，或给定的a，求出h0s②根据2MMf=→ααbhα=10scs2αfbh10c③根据求αξ=112−−≤αξssb④f⑤判别计算出的As是否少筋，即cA=αξbhs10Ahfsy≥≥ρρ或Abhminsminbhh00 2.截面复核已知：M、b、h、As混凝土等级，钢筋级别，求Mu解：①根据环境类别，或给定的a，求出h0sMu若大于M很多，则截面设计②根据αfbx=fA→求出x1cys不经济；③判别结构设计要避免超筋、少筋的x≤x=ξh脆性破坏bb0板的经济配筋率0.3～0.8％，梁0.6～1.5％④M=αfbx(h−0.5x)——若满足，即不超筋u1c02M=αfbhξ(1−0.5ξ)——若不满足，即超筋u,max1c0bb⑤当M≥M时，安全，否则不安全u